![]() Hoe om die omtrek van 'n sirkel presies te bereken?
Hoe om die omtrek van 'n sirkel presies te bereken?
![]() Die omtrek van 'n sirkel is 'n basiese en vereiste wiskundekennis wat in laer- of middelskool bekendgestel word. Om die omtrek van 'n sirkel te bemeester is noodsaaklik vir studente wat beplan om meer gevorderde wiskundekursusse in hoërskool en kollege te volg en vir gestandaardiseerde eksamens soos die SAT en ACT voor te berei.
Die omtrek van 'n sirkel is 'n basiese en vereiste wiskundekennis wat in laer- of middelskool bekendgestel word. Om die omtrek van 'n sirkel te bemeester is noodsaaklik vir studente wat beplan om meer gevorderde wiskundekursusse in hoërskool en kollege te volg en vir gestandaardiseerde eksamens soos die SAT en ACT voor te berei.
![]() Die 10 omtrek van 'n sirkel vasvra in hierdie artikel is ontwerp om jou begrip van die vind van die radius, deursnee en omtrek van 'n sirkel te toets.
Die 10 omtrek van 'n sirkel vasvra in hierdie artikel is ontwerp om jou begrip van die vind van die radius, deursnee en omtrek van 'n sirkel te toets.
![]() Inhoudsopgawe:
Inhoudsopgawe:
 Omtrek van 'n sirkelformule
Omtrek van 'n sirkelformule
![]() Voordat ons 'n toets neem, laat ons 'n paar belangrike inligting saamvat!
Voordat ons 'n toets neem, laat ons 'n paar belangrike inligting saamvat!
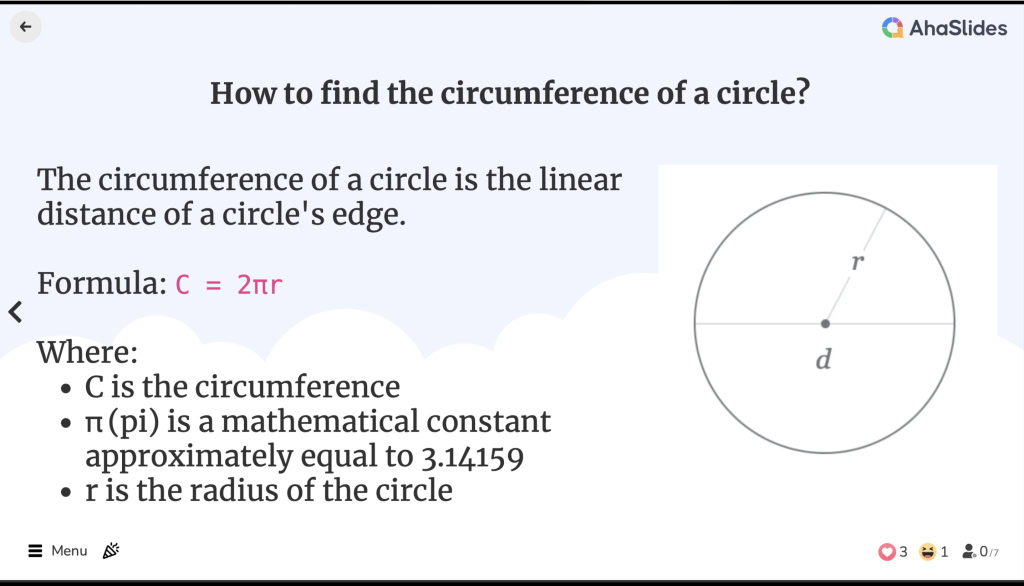
 Hoe om die omtrek van 'n sirkel te vind
Hoe om die omtrek van 'n sirkel te vind![]() Wat is die omtrek van 'n sirkel?
Wat is die omtrek van 'n sirkel?
![]() Die omtrek van 'n sirkel is die lineêre afstand van 'n sirkel se rand. Dit is gelykstaande aan die omtrek van 'n geometriese vorm, hoewel die term omtrek slegs vir veelhoeke gebruik word.
Die omtrek van 'n sirkel is die lineêre afstand van 'n sirkel se rand. Dit is gelykstaande aan die omtrek van 'n geometriese vorm, hoewel die term omtrek slegs vir veelhoeke gebruik word.
![]() Hoe om die omtrek van 'n sirkel te vind?
Hoe om die omtrek van 'n sirkel te vind?
![]() Die omtrek van 'n sirkelformule is:
Die omtrek van 'n sirkelformule is:
C = 2πr
![]() waar:
waar:
 C is die omtrek
C is die omtrek π (pi) is 'n wiskundige konstante wat ongeveer gelyk is aan 3.14159
π (pi) is 'n wiskundige konstante wat ongeveer gelyk is aan 3.14159 r is die radius van die sirkel
r is die radius van die sirkel
![]() Die radius is die afstand vanaf die middel van die sirkel na enige punt op die rand.
Die radius is die afstand vanaf die middel van die sirkel na enige punt op die rand.
![]() Die deursnee is twee keer die radius, dus kan die omtrek ook uitgedruk word as:
Die deursnee is twee keer die radius, dus kan die omtrek ook uitgedruk word as:
C = πd
![]() waar:
waar:
 d is die deursnee
d is die deursnee
![]() Byvoorbeeld, as die radius van 'n sirkel 5 cm is, dan is die omtrek:
Byvoorbeeld, as die radius van 'n sirkel 5 cm is, dan is die omtrek:
C = 2πr = 2π * 5 cm = 10π cm
![]() ≈ 31.4 cm (afgerond tot 2 desimale plekke)
≈ 31.4 cm (afgerond tot 2 desimale plekke)
 Meer wenke van AhaSlides
Meer wenke van AhaSlides
 70+ Wiskundevasvra-vrae vir prettige oefeninge in die klas
70+ Wiskundevasvra-vrae vir prettige oefeninge in die klas 10 Beste Klaskamer Wiskunde-speletjies vir verveelde K12-studente
10 Beste Klaskamer Wiskunde-speletjies vir verveelde K12-studente 60 Awesome Idees Op Brein Teasers Vir Volwassenes | 2023-opdaterings
60 Awesome Idees Op Brein Teasers Vir Volwassenes | 2023-opdaterings
![]() AhaSlides is The Ultimate Quiz Maker
AhaSlides is The Ultimate Quiz Maker
![]() Maak interaktiewe speletjies in 'n kits met ons uitgebreide sjabloonbiblioteek om verveling dood te maak
Maak interaktiewe speletjies in 'n kits met ons uitgebreide sjabloonbiblioteek om verveling dood te maak

 Aanlyn speletjies om te speel as jy verveeld is
Aanlyn speletjies om te speel as jy verveeld is Omtrek van 'n sirkelvasvra
Omtrek van 'n sirkelvasvra
![]() Vraag 1: As die omtrek van 'n sirkelvormige swembad 50 meter is, wat is die radius daarvan?
Vraag 1: As die omtrek van 'n sirkelvormige swembad 50 meter is, wat is die radius daarvan?
![]() A. 7.95 meter
A. 7.95 meter
![]() B. 8.00 meter
B. 8.00 meter
![]() C. 15.91 meter
C. 15.91 meter
![]() D. 25 meter
D. 25 meter
✅ ![]() Korrekte antwoord:
Korrekte antwoord:
![]() A. 7.95 meter
A. 7.95 meter
![]() Verduideliking:
Verduideliking:
![]() Die radius kan gevind word deur die formule C = 2πr te herrangskik en vir r op te los: r = C / (2π). As ons die gegewe omtrek van 50 meter inprop en π benader tot 3.14, vind ons dat die radius ongeveer 7.95 meter is.
Die radius kan gevind word deur die formule C = 2πr te herrangskik en vir r op te los: r = C / (2π). As ons die gegewe omtrek van 50 meter inprop en π benader tot 3.14, vind ons dat die radius ongeveer 7.95 meter is.
![]() Vraag 2: Die deursnee van 'n sirkel is 14 duim. Wat is sy radius?
Vraag 2: Die deursnee van 'n sirkel is 14 duim. Wat is sy radius?
![]() A. 28 duim
A. 28 duim
![]() B.14 duim
B.14 duim
![]() C. 21 duim
C. 21 duim
![]() D. 7 duim
D. 7 duim
✅ ![]() Korrekte antwoord:
Korrekte antwoord:
![]() D. 7 duim
D. 7 duim
![]() Verduideliking:
Verduideliking:
![]() Aangesien die deursnee twee keer die lengte van die radius is (d = 2r), kan jy die radius vind deur die deursnee deur 2 (r = d / 2) te deel. In hierdie geval lewer die gegewe deursnee van 14 duim deur 2 'n radius van 7 duim.
Aangesien die deursnee twee keer die lengte van die radius is (d = 2r), kan jy die radius vind deur die deursnee deur 2 (r = d / 2) te deel. In hierdie geval lewer die gegewe deursnee van 14 duim deur 2 'n radius van 7 duim.

 Vind die omtrek van 'n sirkel
Vind die omtrek van 'n sirkel![]() Vraag 3: Watter van die volgende stellings is waar oor die verwantskap tussen die deursnee en die omtrek van 'n sirkel?
Vraag 3: Watter van die volgende stellings is waar oor die verwantskap tussen die deursnee en die omtrek van 'n sirkel?
![]() A. Die deursnee is die helfte van die omtrek.
A. Die deursnee is die helfte van die omtrek.
![]() B. Die deursnee is dieselfde as die omtrek.
B. Die deursnee is dieselfde as die omtrek.
![]() C. Die deursnee is twee keer die omtrek.
C. Die deursnee is twee keer die omtrek.
![]() D. Die deursnee is π keer die omtrek.
D. Die deursnee is π keer die omtrek.
✅ ![]() Korrekte antwoord:
Korrekte antwoord:
![]() A. Die deursnee is die helfte van die omtrek.
A. Die deursnee is die helfte van die omtrek.
![]() Verduideliking:
Verduideliking:
![]() Die deursnee is gelyk aan 2 keer die radius, terwyl die omtrek gelyk is aan 2π keer die radius. Daarom is die deursnee die helfte van die omtrek.
Die deursnee is gelyk aan 2 keer die radius, terwyl die omtrek gelyk is aan 2π keer die radius. Daarom is die deursnee die helfte van die omtrek.
![]() Vraag 4: Die tafel waarby ons moet sit, het 'n omtrek van 6.28 meter. Ons moet die deursnee van die tafel vind.
Vraag 4: Die tafel waarby ons moet sit, het 'n omtrek van 6.28 meter. Ons moet die deursnee van die tafel vind.
![]() A. 1 jaart
A. 1 jaart
![]() B. 2 meter
B. 2 meter
![]() C. 3 meter
C. 3 meter
![]() D. 4 meter
D. 4 meter
✅ ![]() Korrekte antwoord:
Korrekte antwoord:
![]() B. 2 meter
B. 2 meter
![]() Verduideliking:
Verduideliking:
![]() Die omtrek van 'n sirkel word bereken deur die deursnee met pi (π) te vermenigvuldig. In hierdie geval word die omtrek gegee as 6.28 meter. Om die deursnee te vind, moet ons die omtrek deur pi deel. Deur 6.28 meter deur pi te deel, gee ons ongeveer 2 meter. Daarom is die deursnee van die tafel 2 meter.
Die omtrek van 'n sirkel word bereken deur die deursnee met pi (π) te vermenigvuldig. In hierdie geval word die omtrek gegee as 6.28 meter. Om die deursnee te vind, moet ons die omtrek deur pi deel. Deur 6.28 meter deur pi te deel, gee ons ongeveer 2 meter. Daarom is die deursnee van die tafel 2 meter.
![]() Vraag 5: 'n Sirkelvormige tuin het 'n omtrek van 36 meter. Wat is die benaderde radius van die tuin?
Vraag 5: 'n Sirkelvormige tuin het 'n omtrek van 36 meter. Wat is die benaderde radius van die tuin?
![]() A. 3.14 meter
A. 3.14 meter
![]() B. 6 meter
B. 6 meter
![]() C. 9 meter
C. 9 meter
![]() D. 18 meter
D. 18 meter
✅ ![]() Korrekte antwoord:
Korrekte antwoord:
![]() C. 9 meter
C. 9 meter
![]() Verduideliking:
Verduideliking:
![]() Om die radius te vind, gebruik die formule vir omtrek: C = 2πr. Herrangskik die formule om vir die radius op te los: r = C / (2π). As jy die gegewe omtrek van 36 meter inprop en 'n benaderde waarde van π as 3.14 gebruik, kry jy r = 36 / (2 * 3.14) ≈ 9 meter.
Om die radius te vind, gebruik die formule vir omtrek: C = 2πr. Herrangskik die formule om vir die radius op te los: r = C / (2π). As jy die gegewe omtrek van 36 meter inprop en 'n benaderde waarde van π as 3.14 gebruik, kry jy r = 36 / (2 * 3.14) ≈ 9 meter.
![]() Vraag 6: 'n Sirkelvormige swembad het 'n radius van 8 meter. Wat is die benaderde afstand wat 'n swemmer om die swembad aflê wanneer hy een rondte voltooi?
Vraag 6: 'n Sirkelvormige swembad het 'n radius van 8 meter. Wat is die benaderde afstand wat 'n swemmer om die swembad aflê wanneer hy een rondte voltooi?
![]() A. 16 meter
A. 16 meter
![]() B. 25 meter
B. 25 meter
![]() C. 50 meter
C. 50 meter
![]() D. 100 meter
D. 100 meter
✅ ![]() Korrekte antwoord:
Korrekte antwoord:
![]() C. 50 meter
C. 50 meter
![]() Verduideliking:
Verduideliking:
![]() Om die afstand te vind wat 'n swemmer vir een rondte om die swembad aflê, gebruik jy die omtrekformule (C = 2πr). In hierdie geval is dit 2 * 3.14 * 8 meter ≈ 50.24 meter, wat ongeveer 50 meter is.
Om die afstand te vind wat 'n swemmer vir een rondte om die swembad aflê, gebruik jy die omtrekformule (C = 2πr). In hierdie geval is dit 2 * 3.14 * 8 meter ≈ 50.24 meter, wat ongeveer 50 meter is.
![]() Vraag 7: Toe die hoelahoepel in die klas gemeet is, het groep C ontdek dat dit 'n radius van 7 duim het. Wat is die omtrek van die hoelahoepel?
Vraag 7: Toe die hoelahoepel in die klas gemeet is, het groep C ontdek dat dit 'n radius van 7 duim het. Wat is die omtrek van die hoelahoepel?
![]() A. 39.6 duim
A. 39.6 duim
![]() B. 37.6 duim
B. 37.6 duim
![]() C. 47.6 duim
C. 47.6 duim
![]() D. 49.6 duim
D. 49.6 duim
✅ ![]() Korrekte antwoord:
Korrekte antwoord:
![]() C. 47.6 duim
C. 47.6 duim
![]() Verduideliking:
Verduideliking:
![]() Die omtrek van 'n sirkel kan gevind word deur die formule C = 2πr te gebruik, waar r die radius van die sirkel is. In hierdie geval word die radius van die hoelahoepel as 7 duim gegee. As ons hierdie waarde by die formule inprop, kry ons C = 2π(7) = 14π duim. As ons π tot 3.14 benader, kan ons die omtrek bereken as 14(3.14) = 43.96 duim. Afgerond tot die naaste tiende, is die omtrek 47.6 duim, wat ooreenstem met die gegewe antwoord.
Die omtrek van 'n sirkel kan gevind word deur die formule C = 2πr te gebruik, waar r die radius van die sirkel is. In hierdie geval word die radius van die hoelahoepel as 7 duim gegee. As ons hierdie waarde by die formule inprop, kry ons C = 2π(7) = 14π duim. As ons π tot 3.14 benader, kan ons die omtrek bereken as 14(3.14) = 43.96 duim. Afgerond tot die naaste tiende, is die omtrek 47.6 duim, wat ooreenstem met die gegewe antwoord.
![]() Vraag 8: 'n Halfsirkel het 'n radius van 10 meter. Wat is sy omtrek?
Vraag 8: 'n Halfsirkel het 'n radius van 10 meter. Wat is sy omtrek?
![]() A. 20 meter
A. 20 meter
![]() B. 15 meter
B. 15 meter
![]() C. 31.42 meter
C. 31.42 meter
![]() D. 62.84 meter
D. 62.84 meter
✅ ![]() Korrekte antwoord:
Korrekte antwoord:
![]() C. 31.42 meter
C. 31.42 meter
![]() Verduideliking:
Verduideliking:![]() Om die omtrek van die halfsirkel te vind, bereken die helfte van die omtrek van 'n volle sirkel met 'n radius van 10 meter.
Om die omtrek van die halfsirkel te vind, bereken die helfte van die omtrek van 'n volle sirkel met 'n radius van 10 meter.

 Omtrek van 'n sirkel voorbeeld
Omtrek van 'n sirkel voorbeeld![]() Vraag 9: Die basketbalspan speel met 'n bal met 'n radius van 5.6 duim. Wat is die omtrek van elke basketbal?
Vraag 9: Die basketbalspan speel met 'n bal met 'n radius van 5.6 duim. Wat is die omtrek van elke basketbal?
![]() A. 11.2 duim
A. 11.2 duim
![]() B. 17.6 duim
B. 17.6 duim
![]() C. 22.4 duim
C. 22.4 duim
![]() D. 35.2 duim
D. 35.2 duim
✅ ![]() Korrekte antwoord:
Korrekte antwoord:
![]() C. 22.4 duim
C. 22.4 duim
![]() Verduideliking:
Verduideliking:
![]() Jy kan die formule gebruik vir die omtrek van 'n sirkel, wat C = 2πr is. Die gegewe radius is 5.6 duim. Prop hierdie waarde in die formule, ons het C = 2π * 5.6 duim. C ≈ 2 * 3.14 * 5.6 duim. C ≈ 11.2 * 5.6 duim. C ≈ 22.4 duim. Dus, die omtrek van elke basketbal is ongeveer 22.4 duim. Dit verteenwoordig die afstand rondom die basketbal.
Jy kan die formule gebruik vir die omtrek van 'n sirkel, wat C = 2πr is. Die gegewe radius is 5.6 duim. Prop hierdie waarde in die formule, ons het C = 2π * 5.6 duim. C ≈ 2 * 3.14 * 5.6 duim. C ≈ 11.2 * 5.6 duim. C ≈ 22.4 duim. Dus, die omtrek van elke basketbal is ongeveer 22.4 duim. Dit verteenwoordig die afstand rondom die basketbal.
![]() Vraag 10: Sarah en haar twee vriende was besig om 'n sirkelvormige piekniektafel vir hul byeenkoms te bou. Hulle het geweet dat hulle 'n omtrek van 18 voet nodig het om almal gemaklik om die tafel te kan sit. Watter deursnee moet die piekniektafel hê om die korrekte omtrek te bereik?
Vraag 10: Sarah en haar twee vriende was besig om 'n sirkelvormige piekniektafel vir hul byeenkoms te bou. Hulle het geweet dat hulle 'n omtrek van 18 voet nodig het om almal gemaklik om die tafel te kan sit. Watter deursnee moet die piekniektafel hê om die korrekte omtrek te bereik?
![]() A. 3 voet
A. 3 voet
![]() B. 6 voet
B. 6 voet
![]() C. 9 voet
C. 9 voet
![]() D. 12 voet
D. 12 voet
✅ ![]() Korrekte antwoord:
Korrekte antwoord:
![]() B. 6 voet
B. 6 voet
![]() Verduideliking:
Verduideliking:
![]() Om die radius te vind, deel die omtrek deur 2π, ons het r = C / (2π) r = 18 voet / (2 * 3.14) r ≈ 18 voet / 6.28 r ≈ 2.87 voet (afgerond tot die naaste honderdste).
Om die radius te vind, deel die omtrek deur 2π, ons het r = C / (2π) r = 18 voet / (2 * 3.14) r ≈ 18 voet / 6.28 r ≈ 2.87 voet (afgerond tot die naaste honderdste).
![]() Nou, om die deursnee te vind, verdubbel eenvoudig die radius: Deursnee = 2 * Radius Deursnee ≈ 2 * 2.87 voet Diameter ≈ 5.74 voet. Dus, die piekniektafel moet 'n deursnee van ongeveer 5.74 voet hê
Nou, om die deursnee te vind, verdubbel eenvoudig die radius: Deursnee = 2 * Radius Deursnee ≈ 2 * 2.87 voet Diameter ≈ 5.74 voet. Dus, die piekniektafel moet 'n deursnee van ongeveer 5.74 voet hê
 Belangrike takeaways
Belangrike takeaways
![]() AhaSlides
AhaSlides ![]() is die beste interaktiewe vasvra-maker wat hoed vir onderwys-, opleiding- of vermaakdoeleindes gebruik kan word. Kyk uit AhaSlides dadelik om vry te kom
is die beste interaktiewe vasvra-maker wat hoed vir onderwys-, opleiding- of vermaakdoeleindes gebruik kan word. Kyk uit AhaSlides dadelik om vry te kom ![]() aanpasbare sjablone
aanpasbare sjablone![]() en gevorderde funksies!
en gevorderde funksies!
 Algemene vrae
Algemene vrae
![]() Wat is 2πr van 'n sirkel?
Wat is 2πr van 'n sirkel?
![]() 2πr is die formule vir die omtrek van 'n sirkel. In hierdie formule:
2πr is die formule vir die omtrek van 'n sirkel. In hierdie formule:
 "2" verteenwoordig dat jy twee keer die lengte van die radius neem. Die omtrek is die afstand om die sirkel, so jy moet een keer om die sirkel gaan, en daarom vermenigvuldig ons met 2.
"2" verteenwoordig dat jy twee keer die lengte van die radius neem. Die omtrek is die afstand om die sirkel, so jy moet een keer om die sirkel gaan, en daarom vermenigvuldig ons met 2. "π" (pi) is 'n wiskundige konstante wat ongeveer gelyk is aan 3.14159. Dit word gebruik omdat dit die verhouding tussen die omtrek en die deursnee van 'n sirkel voorstel.
"π" (pi) is 'n wiskundige konstante wat ongeveer gelyk is aan 3.14159. Dit word gebruik omdat dit die verhouding tussen die omtrek en die deursnee van 'n sirkel voorstel. "r" verteenwoordig die radius van die sirkel, wat die afstand is vanaf die middel van die sirkel na enige punt op sy omtrek.
"r" verteenwoordig die radius van die sirkel, wat die afstand is vanaf die middel van die sirkel na enige punt op sy omtrek.
![]() Hoekom is omtrek 2πr?
Hoekom is omtrek 2πr?
![]() Die formule vir die omtrek van 'n sirkel, C = 2πr, kom van die definisie van pi (π) en die geometriese eienskappe van 'n sirkel. Pi (π) verteenwoordig die verhouding van die omtrek van 'n sirkel tot sy deursnee. Wanneer jy die radius (r) met 2π vermenigvuldig, bereken jy in wese die afstand om die sirkel, wat die definisie van omtrek is.
Die formule vir die omtrek van 'n sirkel, C = 2πr, kom van die definisie van pi (π) en die geometriese eienskappe van 'n sirkel. Pi (π) verteenwoordig die verhouding van die omtrek van 'n sirkel tot sy deursnee. Wanneer jy die radius (r) met 2π vermenigvuldig, bereken jy in wese die afstand om die sirkel, wat die definisie van omtrek is.
![]() Is die omtrek 3.14 keer die radius?
Is die omtrek 3.14 keer die radius?
![]() Nee, die omtrek is nie presies 3.14 keer die radius nie. Die verband tussen die omtrek en die radius van 'n sirkel word gegee deur die formule C = 2πr. Terwyl π (pi) ongeveer 3.14159 is, is die omtrek 2 keer π keer die radius. Dus, die omtrek is meer as net 3.14 keer die radius; dit is 2 keer π keer die radius.
Nee, die omtrek is nie presies 3.14 keer die radius nie. Die verband tussen die omtrek en die radius van 'n sirkel word gegee deur die formule C = 2πr. Terwyl π (pi) ongeveer 3.14159 is, is die omtrek 2 keer π keer die radius. Dus, die omtrek is meer as net 3.14 keer die radius; dit is 2 keer π keer die radius.
![]() Ref:
Ref: ![]() Omni Sakrekenaar |
Omni Sakrekenaar | ![]() Prof
Prof







