![]() Mae holiaduron yn gydiwr ar gyfer crynhoi manylion gan bobl ledled y lle.
Mae holiaduron yn gydiwr ar gyfer crynhoi manylion gan bobl ledled y lle.
![]() Er bod holiaduron ym mhobman, nid yw pobl yn siŵr o hyd pa fathau o ymholiadau i'w hychwanegu.
Er bod holiaduron ym mhobman, nid yw pobl yn siŵr o hyd pa fathau o ymholiadau i'w hychwanegu.
![]() Byddwn yn dangos y mathau cyffredin o holiaduron i chi mewn ymchwil, yn ogystal â sut a ble i ddefnyddio un.
Byddwn yn dangos y mathau cyffredin o holiaduron i chi mewn ymchwil, yn ogystal â sut a ble i ddefnyddio un.
![]() Gadewch i ni neidio i mewn 👇
Gadewch i ni neidio i mewn 👇
 Mwy o Awgrymiadau gydag AhaSlides
Mwy o Awgrymiadau gydag AhaSlides
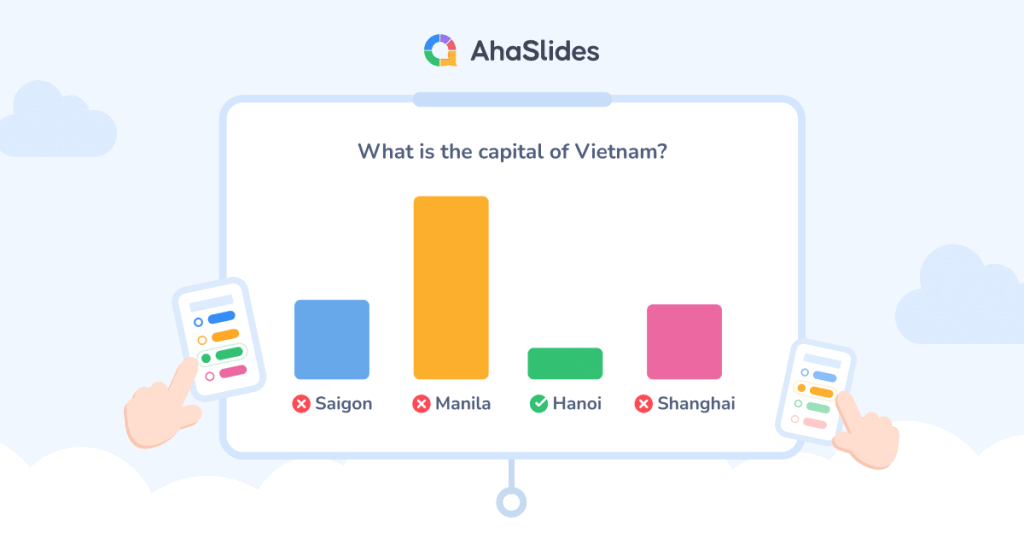
 Mathau o Holiaduron mewn Ymchwil
Mathau o Holiaduron mewn Ymchwil
![]() Wrth wneud eich holiadur, mae'n rhaid i chi feddwl pa fath o wybodaeth rydych chi'n ceisio ei chael gan bobl.
Wrth wneud eich holiadur, mae'n rhaid i chi feddwl pa fath o wybodaeth rydych chi'n ceisio ei chael gan bobl.
![]() Os ydych chi eisiau manylion cyfoethog, archwiliadol i helpu i brofi neu chwalu damcaniaeth, ewch ag arolwg ansoddol gyda chwestiynau penagored. Mae hyn yn gadael i bobl egluro eu meddyliau yn rhydd.
Os ydych chi eisiau manylion cyfoethog, archwiliadol i helpu i brofi neu chwalu damcaniaeth, ewch ag arolwg ansoddol gyda chwestiynau penagored. Mae hyn yn gadael i bobl egluro eu meddyliau yn rhydd.
![]() Ond os oes gennych chi ragdybiaeth yn barod a dim ond angen rhifau i'w brofi, holiadur meintiol yw'r jam. Defnyddiwch gwestiynau caeedig lle mae pobl yn dewis atebion i gael ystadegau mesuradwy, mesuradwy.
Ond os oes gennych chi ragdybiaeth yn barod a dim ond angen rhifau i'w brofi, holiadur meintiol yw'r jam. Defnyddiwch gwestiynau caeedig lle mae pobl yn dewis atebion i gael ystadegau mesuradwy, mesuradwy.
![]() Unwaith y byddwch wedi ei gael, nawr mae'n bryd dewis pa fath o holiadur mewn ymchwil yr hoffech ei gynnwys.
Unwaith y byddwch wedi ei gael, nawr mae'n bryd dewis pa fath o holiadur mewn ymchwil yr hoffech ei gynnwys.
 Mathau o holiadur mewn ymchwil
Mathau o holiadur mewn ymchwil # 1.
# 1.  Holiaduron penagored
Holiaduron penagored
 Mathau o holiaduron mewn ymchwil - Penagored
Mathau o holiaduron mewn ymchwil - Penagored![]() Mae cwestiynau penagored yn arf gwerthfawr mewn ymchwil gan eu bod yn caniatáu i bynciau fynegi eu safbwyntiau yn llawn heb gyfyngiadau.
Mae cwestiynau penagored yn arf gwerthfawr mewn ymchwil gan eu bod yn caniatáu i bynciau fynegi eu safbwyntiau yn llawn heb gyfyngiadau.
![]() Mae fformat anstrwythuredig cwestiynau penagored, nad ydynt yn darparu dewisiadau ateb wedi'u diffinio ymlaen llaw, yn eu gwneud yn addas iawn ar gyfer ymchwil archwiliadol yn gynnar.
Mae fformat anstrwythuredig cwestiynau penagored, nad ydynt yn darparu dewisiadau ateb wedi'u diffinio ymlaen llaw, yn eu gwneud yn addas iawn ar gyfer ymchwil archwiliadol yn gynnar.
![]() Mae hyn yn galluogi ymchwilwyr i ddod o hyd i fewnwelediadau cynnil ac o bosibl nodi llwybrau newydd ar gyfer ymchwilio na chawsant eu llunio o'r blaen.
Mae hyn yn galluogi ymchwilwyr i ddod o hyd i fewnwelediadau cynnil ac o bosibl nodi llwybrau newydd ar gyfer ymchwilio na chawsant eu llunio o'r blaen.
![]() Er bod cwestiynau penagored yn cynhyrchu data ansoddol yn hytrach na meintiol, sy'n gofyn am ddulliau codio mwy manwl ar gyfer dadansoddi samplau mawr, eu cryfder yw datgelu ystod eang o ymatebion meddylgar.
Er bod cwestiynau penagored yn cynhyrchu data ansoddol yn hytrach na meintiol, sy'n gofyn am ddulliau codio mwy manwl ar gyfer dadansoddi samplau mawr, eu cryfder yw datgelu ystod eang o ymatebion meddylgar.
![]() Yn cael eu defnyddio’n gyffredin fel cwestiynau rhagarweiniol mewn cyfweliadau neu astudiaethau peilot i archwilio ffactorau esboniadol, mae ymholiadau penagored yn fwyaf defnyddiol pan fo angen deall pwnc o bob ongl cyn dylunio arolygon cwestiwn caeedig mwy uniongyrchol.
Yn cael eu defnyddio’n gyffredin fel cwestiynau rhagarweiniol mewn cyfweliadau neu astudiaethau peilot i archwilio ffactorau esboniadol, mae ymholiadau penagored yn fwyaf defnyddiol pan fo angen deall pwnc o bob ongl cyn dylunio arolygon cwestiwn caeedig mwy uniongyrchol.
![]() enghraifft:
enghraifft:
![]() Cwestiynau barn:
Cwestiynau barn:
![What are your thoughts on [topic]?](//tdns.gtranslate.net/tdn-static2/images/edit.png) Beth yw eich barn ar [pwnc]?
Beth yw eich barn ar [pwnc]?![How would you describe your experience with [topic]?](//tdns.gtranslate.net/tdn-static2/images/edit.png) Sut byddech chi'n disgrifio'ch profiad gyda [pwnc]?
Sut byddech chi'n disgrifio'ch profiad gyda [pwnc]?
![]() Cwestiynau profiad:
Cwestiynau profiad:
![Tell me about a time when [event] occurred.](//tdns.gtranslate.net/tdn-static2/images/edit.png) Dywedwch wrthyf am adeg pan ddigwyddodd [digwyddiad].
Dywedwch wrthyf am adeg pan ddigwyddodd [digwyddiad].![Walk me through the process of [activity].](//tdns.gtranslate.net/tdn-static2/images/edit.png) Cerddwch fi drwy'r broses o [gweithgarwch].
Cerddwch fi drwy'r broses o [gweithgarwch].
![]() Cwestiynau teimlad:
Cwestiynau teimlad:
![How did you feel about [event/situation]?](//tdns.gtranslate.net/tdn-static2/images/edit.png) Sut oeddech chi'n teimlo am [digwyddiad/sefyllfa]?
Sut oeddech chi'n teimlo am [digwyddiad/sefyllfa]?![What emotions are evoked when [stimulus] is present?](//tdns.gtranslate.net/tdn-static2/images/edit.png) Pa emosiynau sy'n cael eu creu pan fydd [ysgogiad] yn bresennol?
Pa emosiynau sy'n cael eu creu pan fydd [ysgogiad] yn bresennol?
![]() Cwestiynau argymhelliad:
Cwestiynau argymhelliad:
![How could [issue] be improved?](//tdns.gtranslate.net/tdn-static2/images/edit.png) Sut y gellid gwella [mater]?
Sut y gellid gwella [mater]?![What suggestions do you have for [proposed solution/idea]?](//tdns.gtranslate.net/tdn-static2/images/edit.png) Pa awgrymiadau sydd gennych ar gyfer [ateb/syniad arfaethedig]?
Pa awgrymiadau sydd gennych ar gyfer [ateb/syniad arfaethedig]?
![]() Cwestiynau effaith:
Cwestiynau effaith:
![In what ways has [event] affected you?](//tdns.gtranslate.net/tdn-static2/images/edit.png) Ym mha ffyrdd mae [digwyddiad] wedi effeithio arnoch chi?
Ym mha ffyrdd mae [digwyddiad] wedi effeithio arnoch chi?![How have your views on [topic] changed over time?](//tdns.gtranslate.net/tdn-static2/images/edit.png) Sut mae eich barn ar [destun] wedi newid dros amser?
Sut mae eich barn ar [destun] wedi newid dros amser?
![]() Cwestiynau damcaniaethol:
Cwestiynau damcaniaethol:
![How do you think you would react if [scenario]?](//tdns.gtranslate.net/tdn-static2/images/edit.png) Sut ydych chi'n meddwl y byddech chi'n ymateb pe bai [senario]?
Sut ydych chi'n meddwl y byddech chi'n ymateb pe bai [senario]?![What factors do you think would influence [outcome]?](//tdns.gtranslate.net/tdn-static2/images/edit.png) Pa ffactorau ydych chi'n meddwl fyddai'n dylanwadu ar [canlyniad]?
Pa ffactorau ydych chi'n meddwl fyddai'n dylanwadu ar [canlyniad]?
![]() Cwestiynau dehongli:
Cwestiynau dehongli:
![What does [term] mean to you?](//tdns.gtranslate.net/tdn-static2/images/edit.png) Beth mae [term] yn ei olygu i chi?
Beth mae [term] yn ei olygu i chi?![How would you interpret the finding that [result]?](//tdns.gtranslate.net/tdn-static2/images/edit.png) Sut byddech chi'n dehongli'r canfyddiad hwnnw [canlyniad]?
Sut byddech chi'n dehongli'r canfyddiad hwnnw [canlyniad]?
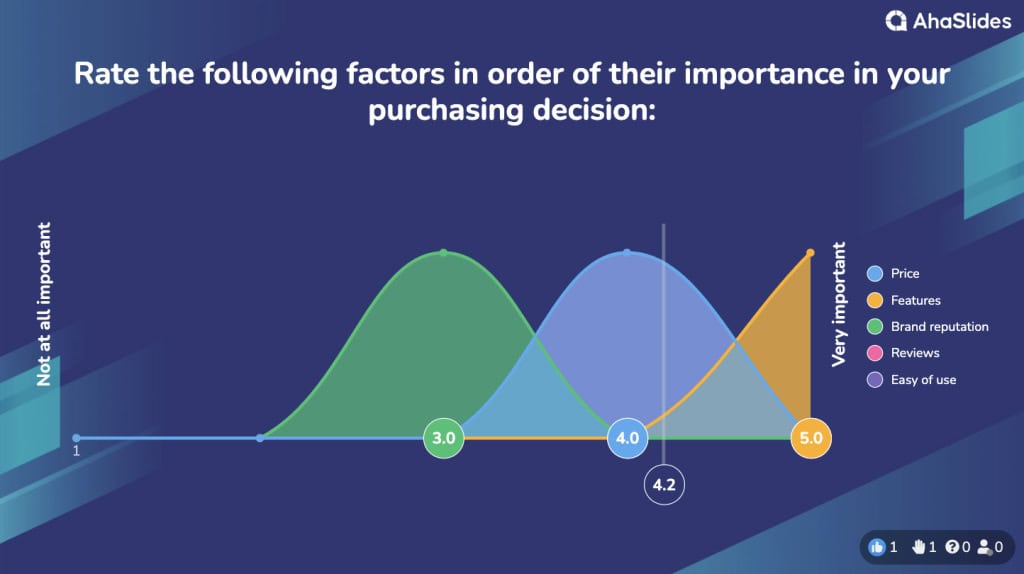
 #2. Holiaduron graddfa raddio
#2. Holiaduron graddfa raddio
 Mathau o holiadur mewn ymchwil - Graddfa fesur
Mathau o holiadur mewn ymchwil - Graddfa fesur![]() Mae cwestiynau graddfa sgorio yn arf gwerthfawr mewn ymchwil ar gyfer mesur agweddau, barn, a chanfyddiadau sy'n bodoli ar gontinwwm yn hytrach nag fel cyflyrau absoliwt.
Mae cwestiynau graddfa sgorio yn arf gwerthfawr mewn ymchwil ar gyfer mesur agweddau, barn, a chanfyddiadau sy'n bodoli ar gontinwwm yn hytrach nag fel cyflyrau absoliwt.
![]() Trwy gyflwyno cwestiwn wedi'i ddilyn gan raddfa wedi'i rhifo i ymatebwyr nodi lefel eu cytundeb, pwysigrwydd, boddhad, neu raddau eraill, mae'r cwestiynau hyn yn nodi dwyster neu gyfeiriad teimladau mewn ffordd strwythuredig ond cynnil.
Trwy gyflwyno cwestiwn wedi'i ddilyn gan raddfa wedi'i rhifo i ymatebwyr nodi lefel eu cytundeb, pwysigrwydd, boddhad, neu raddau eraill, mae'r cwestiynau hyn yn nodi dwyster neu gyfeiriad teimladau mewn ffordd strwythuredig ond cynnil.
![]() Mae mathau cyffredin yn cynnwys
Mae mathau cyffredin yn cynnwys ![]() Graddfeydd Likert
Graddfeydd Likert![]() cynnwys labeli fel anghytuno'n gryf i gytuno'n gryf yn ogystal â graddfeydd analog gweledol.
cynnwys labeli fel anghytuno'n gryf i gytuno'n gryf yn ogystal â graddfeydd analog gweledol.
![]() Yna gellir yn hawdd agregu'r data metrig meintiol a ddarperir ganddynt a'u dadansoddi'n ystadegol i gymharu graddfeydd cymedrig, cydberthnasau a pherthnasoedd.
Yna gellir yn hawdd agregu'r data metrig meintiol a ddarperir ganddynt a'u dadansoddi'n ystadegol i gymharu graddfeydd cymedrig, cydberthnasau a pherthnasoedd.
![]() Mae graddfeydd graddio yn addas iawn ar gyfer cymwysiadau fel dadansoddi segmentiad y farchnad, rhag-brofi, a gwerthuso rhaglenni ôl-weithredu trwy dechnegau fel
Mae graddfeydd graddio yn addas iawn ar gyfer cymwysiadau fel dadansoddi segmentiad y farchnad, rhag-brofi, a gwerthuso rhaglenni ôl-weithredu trwy dechnegau fel ![]() Profi A/B.
Profi A/B.
![]() Er ei bod yn bosibl bod eu natur gostyngol yn brin o gyd-destun ymatebion agored, mae graddfeydd graddio yn dal i fesur dimensiynau teimlad yn effeithlon ar gyfer archwilio'r cysylltiadau rhagfynegol rhwng agweddau o'u gosod yn briodol ar ôl yr ymholiad disgrifiadol cychwynnol.
Er ei bod yn bosibl bod eu natur gostyngol yn brin o gyd-destun ymatebion agored, mae graddfeydd graddio yn dal i fesur dimensiynau teimlad yn effeithlon ar gyfer archwilio'r cysylltiadau rhagfynegol rhwng agweddau o'u gosod yn briodol ar ôl yr ymholiad disgrifiadol cychwynnol.
 #3. Holiaduron caeedig
#3. Holiaduron caeedig
 Mathau o holiaduron mewn ymchwil - Diweddglo
Mathau o holiaduron mewn ymchwil - Diweddglo![]() Defnyddir cwestiynau caeedig yn gyffredin mewn ymchwil i gasglu data meintiol, strwythuredig trwy ddewisiadau ateb safonol.
Defnyddir cwestiynau caeedig yn gyffredin mewn ymchwil i gasglu data meintiol, strwythuredig trwy ddewisiadau ateb safonol.
![]() Trwy ddarparu set gyfyngedig o opsiynau ymateb i bynciau ddewis o’u plith, megis gwir/anghywir, ie/na, graddfeydd graddio neu atebion amlddewis wedi’u diffinio ymlaen llaw, mae cwestiynau caeedig yn rhoi ymatebion y gellir eu codio, eu hagregu a’u dadansoddi’n haws yn haws. ar draws samplau mawr o gymharu â chwestiynau penagored.
Trwy ddarparu set gyfyngedig o opsiynau ymateb i bynciau ddewis o’u plith, megis gwir/anghywir, ie/na, graddfeydd graddio neu atebion amlddewis wedi’u diffinio ymlaen llaw, mae cwestiynau caeedig yn rhoi ymatebion y gellir eu codio, eu hagregu a’u dadansoddi’n haws yn haws. ar draws samplau mawr o gymharu â chwestiynau penagored.
![]() Mae hyn yn eu gwneud yn addas yn ystod cyfnodau dilysu diweddarach ar ôl i ffactorau gael eu nodi eisoes, megis profi damcaniaeth, mesur agweddau neu ganfyddiadau, graddfeydd pwnc, ac ymholiadau disgrifiadol yn dibynnu ar ddata sy'n seiliedig ar ffeithiau.
Mae hyn yn eu gwneud yn addas yn ystod cyfnodau dilysu diweddarach ar ôl i ffactorau gael eu nodi eisoes, megis profi damcaniaeth, mesur agweddau neu ganfyddiadau, graddfeydd pwnc, ac ymholiadau disgrifiadol yn dibynnu ar ddata sy'n seiliedig ar ffeithiau.
![]() Er bod cyfyngu ar ymatebion yn symleiddio’r gwaith arolygu ac yn caniatáu ar gyfer cymharu’n uniongyrchol, mae perygl iddo hepgor materion nas rhagwelwyd neu golli cyd-destun y tu hwnt i’r dewisiadau eraill a roddwyd.
Er bod cyfyngu ar ymatebion yn symleiddio’r gwaith arolygu ac yn caniatáu ar gyfer cymharu’n uniongyrchol, mae perygl iddo hepgor materion nas rhagwelwyd neu golli cyd-destun y tu hwnt i’r dewisiadau eraill a roddwyd.
 #4. Holiaduron amlddewis
#4. Holiaduron amlddewis
 Mathau o holiaduron mewn ymchwil - Amlddewis
Mathau o holiaduron mewn ymchwil - Amlddewis![]() Mae cwestiynau amlddewis yn arf defnyddiol mewn ymchwil pan gânt eu gweinyddu'n gywir trwy holiaduron caeedig.
Mae cwestiynau amlddewis yn arf defnyddiol mewn ymchwil pan gânt eu gweinyddu'n gywir trwy holiaduron caeedig.
![]() Maent yn cyflwyno cwestiwn i ymatebwyr ynghyd â phedwar i bum opsiwn ateb wedi'u diffinio ymlaen llaw i ddewis ohonynt.
Maent yn cyflwyno cwestiwn i ymatebwyr ynghyd â phedwar i bum opsiwn ateb wedi'u diffinio ymlaen llaw i ddewis ohonynt.
![]() Mae'r fformat hwn yn caniatáu ar gyfer meintioli ymatebion yn hawdd y gellir eu dadansoddi'n ystadegol ar draws grwpiau sampl mawr.
Mae'r fformat hwn yn caniatáu ar gyfer meintioli ymatebion yn hawdd y gellir eu dadansoddi'n ystadegol ar draws grwpiau sampl mawr.
![]() Er eu bod yn gyflym i gyfranogwyr eu cwblhau ac yn hawdd i'w codio a'u dehongli, mae rhai cyfyngiadau hefyd i gwestiynau amlddewis.
Er eu bod yn gyflym i gyfranogwyr eu cwblhau ac yn hawdd i'w codio a'u dehongli, mae rhai cyfyngiadau hefyd i gwestiynau amlddewis.
![]() Yn fwyaf nodedig, maent mewn perygl o anwybyddu arlliwiau pwysig neu golli opsiynau perthnasol os na chânt eu profi'n ofalus ymlaen llaw.
Yn fwyaf nodedig, maent mewn perygl o anwybyddu arlliwiau pwysig neu golli opsiynau perthnasol os na chânt eu profi'n ofalus ymlaen llaw.
![]() Er mwyn lleihau'r risg o ragfarn, rhaid i ddewisiadau ateb fod yn annibynnol ar ei gilydd ac yn gynhwysfawr ar y cyd.
Er mwyn lleihau'r risg o ragfarn, rhaid i ddewisiadau ateb fod yn annibynnol ar ei gilydd ac yn gynhwysfawr ar y cyd.
![]() Gydag ystyriaethau ar gyfer geiriad ac opsiynau, gall cwestiynau amlddewis gynhyrchu data disgrifiadol mesuradwy yn effeithlon pan fydd y posibiliadau allweddol yn cael eu nodi ymlaen llaw, megis ar gyfer dosbarthu ymddygiadau, a phroffiliau demograffig neu asesu gwybodaeth ar bynciau lle mae amrywiadau yn hysbys.
Gydag ystyriaethau ar gyfer geiriad ac opsiynau, gall cwestiynau amlddewis gynhyrchu data disgrifiadol mesuradwy yn effeithlon pan fydd y posibiliadau allweddol yn cael eu nodi ymlaen llaw, megis ar gyfer dosbarthu ymddygiadau, a phroffiliau demograffig neu asesu gwybodaeth ar bynciau lle mae amrywiadau yn hysbys.
 #5. Holiaduron ar raddfa Likert
#5. Holiaduron ar raddfa Likert
 Mathau o holiaduron mewn ymchwil - graddfa Likert
Mathau o holiaduron mewn ymchwil - graddfa Likert![]() Mae graddfa Likert yn fath o raddfa Sgorio a ddefnyddir yn gyffredin mewn ymchwil i fesur yn feintiol agweddau, barn a chanfyddiadau ar bynciau amrywiol o ddiddordeb.
Mae graddfa Likert yn fath o raddfa Sgorio a ddefnyddir yn gyffredin mewn ymchwil i fesur yn feintiol agweddau, barn a chanfyddiadau ar bynciau amrywiol o ddiddordeb.
![]() Gan ddefnyddio fformat ymateb cymesurol cytuno-anghytuno lle mae cyfranogwyr yn nodi lefel eu cytundeb â datganiad, mae graddfeydd Likert fel arfer yn cynnwys dyluniad 5 pwynt er bod mwy neu lai o opsiynau yn bosibl yn dibynnu ar y sensitifrwydd mesur angenrheidiol.
Gan ddefnyddio fformat ymateb cymesurol cytuno-anghytuno lle mae cyfranogwyr yn nodi lefel eu cytundeb â datganiad, mae graddfeydd Likert fel arfer yn cynnwys dyluniad 5 pwynt er bod mwy neu lai o opsiynau yn bosibl yn dibynnu ar y sensitifrwydd mesur angenrheidiol.
![]() Trwy aseinio gwerthoedd rhifol i bob lefel o'r raddfa ymateb, mae data Likert yn caniatáu dadansoddiad ystadegol o batrymau a pherthnasoedd rhwng newidynnau.
Trwy aseinio gwerthoedd rhifol i bob lefel o'r raddfa ymateb, mae data Likert yn caniatáu dadansoddiad ystadegol o batrymau a pherthnasoedd rhwng newidynnau.
![]() Mae hyn yn rhoi canlyniadau mwy cyson na chwestiynau ie/na neu benagored syml ar gyfer rhai mathau o gwestiynau sydd wedi’u hanelu at fesur dwyster teimladau ar gontinwwm.
Mae hyn yn rhoi canlyniadau mwy cyson na chwestiynau ie/na neu benagored syml ar gyfer rhai mathau o gwestiynau sydd wedi’u hanelu at fesur dwyster teimladau ar gontinwwm.
![]() Er bod graddfeydd Likert yn darparu data metrig hawdd ei gasglu ac yn syml i ymatebwyr, mae eu cyfyngiad yn gorsymleiddio safbwyntiau cymhleth, er eu bod yn dal i gynnig mewnwelediad gwerthfawr o'u cymhwyso'n briodol mewn ymchwil.
Er bod graddfeydd Likert yn darparu data metrig hawdd ei gasglu ac yn syml i ymatebwyr, mae eu cyfyngiad yn gorsymleiddio safbwyntiau cymhleth, er eu bod yn dal i gynnig mewnwelediad gwerthfawr o'u cymhwyso'n briodol mewn ymchwil.
![]() enghraifft
enghraifft
![]() Mae ymchwilydd eisiau deall y berthynas rhwng boddhad swydd (newidyn dibynnol) a ffactorau fel cyflog, cydbwysedd bywyd a gwaith, ac ansawdd goruchwyliaeth (newidynnau annibynnol).
Mae ymchwilydd eisiau deall y berthynas rhwng boddhad swydd (newidyn dibynnol) a ffactorau fel cyflog, cydbwysedd bywyd a gwaith, ac ansawdd goruchwyliaeth (newidynnau annibynnol).
![]() Defnyddir graddfa Likert 5 pwynt ar gyfer cwestiynau fel:
Defnyddir graddfa Likert 5 pwynt ar gyfer cwestiynau fel:
 Rwy'n fodlon ar fy nghyflog (Anghytuno'n gryf i Gytuno'n gryf)
Rwy'n fodlon ar fy nghyflog (Anghytuno'n gryf i Gytuno'n gryf) Mae fy swydd yn caniatáu cydbwysedd da rhwng bywyd a gwaith (Anghytuno’n gryf i Gytuno’n gryf)
Mae fy swydd yn caniatáu cydbwysedd da rhwng bywyd a gwaith (Anghytuno’n gryf i Gytuno’n gryf) Mae fy ngoruchwyliwr yn gefnogol ac yn rheolwr da (Anghytuno'n gryf i Cytuno'n gryf)
Mae fy ngoruchwyliwr yn gefnogol ac yn rheolwr da (Anghytuno'n gryf i Cytuno'n gryf)
![]() Rydym yn ymdrin â phob math o holiaduron mewn ymchwil.
Rydym yn ymdrin â phob math o holiaduron mewn ymchwil.![]() Dechreuwch ar unwaith gydag AhaSlides '
Dechreuwch ar unwaith gydag AhaSlides ' ![]() templedi arolwg am ddim!
templedi arolwg am ddim!
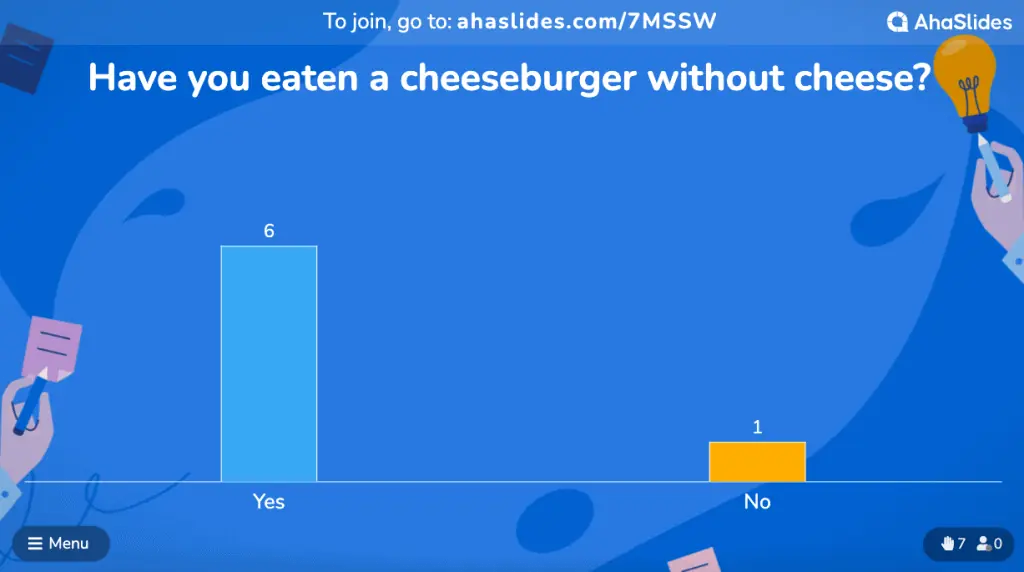
 Siop Cludfwyd Allweddol
Siop Cludfwyd Allweddol
![]() Mae'r mathau hyn o holiaduron ymchwil fel arfer yn gyffredin ac yn hawdd i bobl eu llenwi.
Mae'r mathau hyn o holiaduron ymchwil fel arfer yn gyffredin ac yn hawdd i bobl eu llenwi.
![]() Pan fydd eich ymholiadau'n syml i'w deall a'ch opsiynau'n unffurf, mae pawb ar yr un dudalen. Yna mae'r atebion yn crynhoi'n braf p'un a gawsoch un ymateb neu filiwn.
Pan fydd eich ymholiadau'n syml i'w deall a'ch opsiynau'n unffurf, mae pawb ar yr un dudalen. Yna mae'r atebion yn crynhoi'n braf p'un a gawsoch un ymateb neu filiwn.
![]() Yr allwedd yw gwneud yn siŵr bod ymatebwyr bob amser yn gwybod yn union beth rydych chi'n ei ofyn, ac yna bydd eu hatebion yn llithro i'r dde i'w lle ar gyfer cydosod sgwpiau arolwg melysion yn llyfn.
Yr allwedd yw gwneud yn siŵr bod ymatebwyr bob amser yn gwybod yn union beth rydych chi'n ei ofyn, ac yna bydd eu hatebion yn llithro i'r dde i'w lle ar gyfer cydosod sgwpiau arolwg melysion yn llyfn.
 Cwestiynau Cyffredin
Cwestiynau Cyffredin
![]() Beth yw'r 4 math o holiadur mewn ymchwil?
Beth yw'r 4 math o holiadur mewn ymchwil?
![]() Y pedwar prif fath o holiadur a ddefnyddir mewn ymchwil yw holiaduron strwythuredig, holiaduron anstrwythuredig, arolygon a chyfweliadau. Mae'r math priodol yn dibynnu ar amcanion yr ymchwil, y gyllideb, yr amserlen ac ai dulliau ansoddol, meintiol neu gymysg sydd fwyaf addas.
Y pedwar prif fath o holiadur a ddefnyddir mewn ymchwil yw holiaduron strwythuredig, holiaduron anstrwythuredig, arolygon a chyfweliadau. Mae'r math priodol yn dibynnu ar amcanion yr ymchwil, y gyllideb, yr amserlen ac ai dulliau ansoddol, meintiol neu gymysg sydd fwyaf addas.
![]() Beth yw'r 6 prif fath o gwestiynau arolwg?
Beth yw'r 6 prif fath o gwestiynau arolwg?
![]() Y chwe phrif fath o gwestiynau arolwg yw cwestiynau caeedig, cwestiynau penagored, cwestiynau graddfa raddio, cwestiynau graddfa graddio, cwestiynau demograffig a chwestiynau ymddygiad.
Y chwe phrif fath o gwestiynau arolwg yw cwestiynau caeedig, cwestiynau penagored, cwestiynau graddfa raddio, cwestiynau graddfa graddio, cwestiynau demograffig a chwestiynau ymddygiad.
![]() Beth yw'r tri math o holiadur?
Beth yw'r tri math o holiadur?
![]() Y tri phrif fath o holiadur yw holiaduron strwythuredig, holiaduron lled-strwythuredig a holiaduron distrwythur.
Y tri phrif fath o holiadur yw holiaduron strwythuredig, holiaduron lled-strwythuredig a holiaduron distrwythur.











