10 Ka Poai Poai o ka ninau poai e hooikaika | Nā mea hou 2024

Pehea e helu pono ai i ke anapuni o ka poai?

ʻO ke anapuni o ka pōʻai he ʻike makemakika kumu a koi ʻia i hoʻokomo ʻia ma ke kula haʻahaʻa a waena paha. He mea nui ka hoʻonaʻauao ʻana i ka pōʻai no nā haumāna e hoʻolālā e ʻimi i nā papa makemakika kiʻekiʻe ma ke kula kiʻekiʻe a me ke kulanui a hoʻomākaukau no nā hoʻokolohua maʻamau e like me ka SAT a me ACT.

Ua hoʻolālā ʻia ka 10 Circumference of a Circle Quiz ma kēia ʻatikala e hoʻāʻo i kou ʻike i ka ʻimi ʻana i ka radius, anawaena, a me ke anapuni o kahi pōʻai.

Table of Contents:

Ka pōʻai o ke kaʻina hana
Ka pōʻai o ka pōʻai quiz
ʻO nā lawe waiwai
Pinepine ninau ninaninau 'ana i

Ka pōʻai o ke kaʻina hana

Ma mua o ka lawe ʻana i kahi hoʻokolohua, e hoʻihoʻi hou i kekahi ʻike koʻikoʻi!

pehea e imi ai i ke anapuni o ka poai — *Pehea e ʻike ai i ke anapuni o ka pōʻai*

He aha ke anapuni o ka poai?

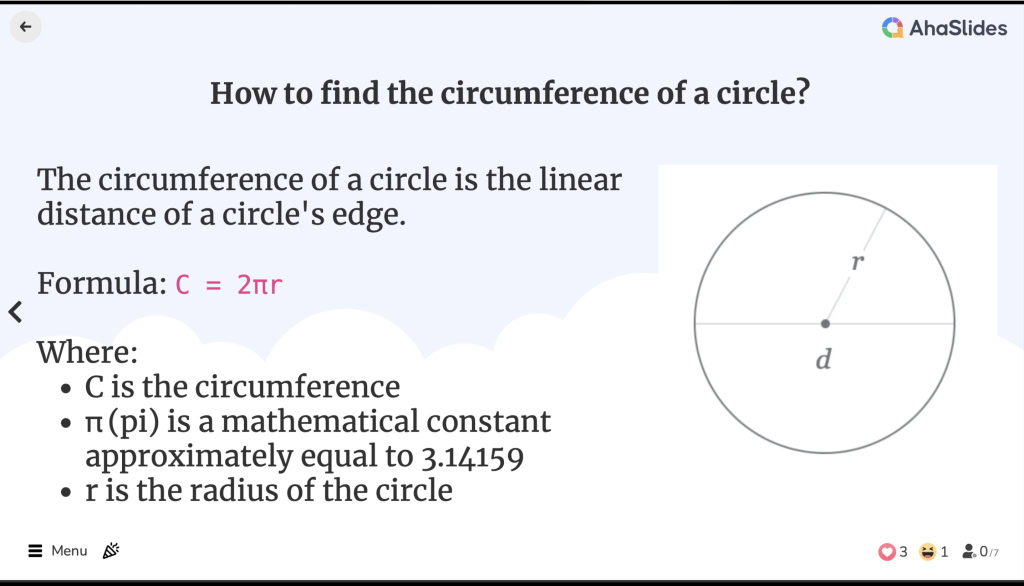
ʻO ke anapuni o ka pōʻai ka lōʻihi laina o ka lihi o ka pōʻai. Ua like ia me ke anapuni o kahi ʻano geometric, ʻoiai ua hoʻohana ʻia ka huaʻōlelo perimeter no nā polygons.

Pehea e ʻike ai i ke anapuni o ka pōʻai?

ʻO ke ʻano o ka pōʻai o ka pōʻai:

C = 2πr

kahi:

ʻO C ke anapuni
π (pi) he makemakika mau ma kahi o 3.14159
r ka radius o ka poai

ʻO ka radius ka mamao mai ke kikowaena o ka pōʻai a i kekahi kiko ma ka lihi.

ʻO ke anawaena ʻelua ka radius, no laila hiki ke hōʻike ʻia ke anapuni penei:

C = πd

kahi:

d ka anawaena

No ka laʻana, inā he 5 knm ka radius o ka pōʻai, a laila ʻo ke anapuni:

C = 2πr = 2π * 5 cm = 10π cm

≈ 31.4 knm (poe ʻia i 2 mau wahi decimal)

Nā ʻōlelo aʻoaʻo hou mai AhaSlides

AhaSlides ʻO ia ka Mea Hana Quiz Loa

E hana i nā pāʻani pāʻani i ka manawa koke me kā mākou waihona hoʻohālike nui e pepehi i ka ʻeha

Ke pāʻani nei ka poʻe i ka nīnau AhaSlides e like me kekahi o nā manaʻo pāʻina pili — *Nā Pāʻani Online e pāʻani ai i ka wā ʻoluʻolu*

GRAB FREE mooolelo

Ka pōʻai o ka pōʻai quiz

Nīnau 1: Inā he 50 mika ke anapuni o ka loko ʻauʻau pōʻai, he aha kona radius?

A. 7.95 mika

B. 8.00 mika

C. 15.91 mika

D. 25 mika

✅ Pane Pololei:

A. 7.95 mika

Hōʻike:

Hiki ke loaʻa ka radius ma ka hoʻonohonoho hou ʻana i ke kumu C = 2πr a me ka hoʻoholo ʻana no r: r = C / (2π). Ke hoʻopili nei i ka pōʻai i hāʻawi ʻia o 50 mika a ma kahi o π i 3.14, ʻike mākou i ka radius ma kahi o 7.95 mau mika.

Ninau 2: He 14 iniha ke anawaena o ka poai. He aha kona radius?

A. 28 iniha

B.14 iniha

C. 21 iniha

D. 7 iniha

✅ Pane Pololei:

D. 7 iniha

Hōʻike:

No ka mea, he palua ke anawaena o ka radius (d = 2r), hiki ke loaa ia oe ke anawaena ma ka puunaue ana i ke anawaena me 2 (r = d / 2). radius o 14 iniha.

e imi i ke anapuni o ka poai — *E imi i ke anapuni o ka poai*

Nīnau 3: ʻO wai ka ʻōlelo ʻoiaʻiʻo e pili ana i ka pilina ma waena o ke anawaena a me ke anapuni o ka pōʻai?

H. O ke anawaena ka hapalua o ke anapuni.

B. Ua like ke anawaena me ke anapuni.

C. Palua ka anawaena o ke anapuni.

D. ʻO ke anawaena he π manawa o ke anapuni.

✅ Pane Pololei:

H. O ke anawaena ka hapalua o ke anapuni.

Hōʻike:

Ua like ke anawaena me 2 manawa o ka radius, oiai ua like ke anapuni me 2π manawa o ka radius. No laila, ʻo ke anawaena ka hapalua o ke anapuni.

Nīnau 4: ʻO ka pākaukau a mākou e noho ai he 6.28 iwilei. Pono mākou e ʻimi i ke anawaena o ka papaʻaina.

A. 1 iwilei

B. 2 iwilei

C. 3 iwilei

D. 4 iwilei

✅ Pane Pololei:

B. 2 iwilei

Hōʻike:

Ua helu ʻia ke anapuni o ka pōʻai ma ka hoʻonui ʻana i ke anawaena me ka pi (π). I kēia hihia, hāʻawi ʻia ke anapuni e like me 6.28 iwilei. No ka loaʻa ʻana o ke anawaena, pono mākou e puʻunaue i ke anapuni me ka pi. ʻO ka puʻunaue ʻana i 6.28 iwilei me ka pi e hāʻawi iā mākou ma kahi o 2 iwilei. No laila, he 2 iwilei ke anawaena o ka papaaina.

Nīnau 5: He 36 mika ka anapuni o ka māla pōʻai. He aha ka radius pili o ka māla?

A. 3.14 mika

B. 6 mika

C. 9 mika

D. 18 mika

✅ Pane Pololei:

C. 9 mika

Hōʻike:

No ka loaʻa ʻana o ka radius, e hoʻohana i ke ʻano no ke anapuni: C = 2πr. E hoʻonohonoho hou i ke kumu e hoʻonā ai no ka radius: r = C / (2π). Ke hoʻopili nei ʻoe i ke anapuni i hāʻawi ʻia o 36 mau mika a me ka hoʻohana ʻana i kahi waiwai kokoke o π me 3.14, loaʻa iā ʻoe r = 36 / (2 * 3.14) ≈ 9 mika.

Nīnau 6: He 8 mika ka radius o ka wai ʻauʻau pōʻai. He aha ka mamao a ka mea ʻauʻau e hele ai a puni ka loko wai i ka wā e hoʻopau ai i hoʻokahi ʻūhā?

A. 16 mika

B. 25 mika

C. 50 mika

D. 100 mika

✅ Pane Pololei:

C. 50 mika

Hōʻike:

No ka huli ʻana i ka mamao a ka mea ʻauʻau e hele ai a puni ka loko wai no ka ʻūhā hoʻokahi, hoʻohana ʻoe i ke ʻano hoʻohālikelike (C = 2πr). I kēia hihia, ʻo ia ka 2 * 3.14 * 8 mika ≈ 50.24 mau mika, ʻo ia ka 50 mika.

Nīnau 7: I ke ana ana i ka hula hoop ma ka papa, ua ike ka hui C he 7 iniha kona radius. He aha ke anapuni o ka hula hoop?

A. 39.6 iniha

B. 37.6 iniha

C. 47.6 iniha

D. 49.6 iniha

✅ Pane Pololei:

C. 47.6 iniha

Hōʻike:

Hiki ke loaʻa ke anapuni o ka pōʻai me ka hoʻohana ʻana i ke ʻano C = 2πr, kahi o r ka radius o ka pōʻai. I kēia hihia, hāʻawi ʻia ka radius o ka hula hoop he 7 ʻīniha. Ke hoʻopili nei i kēia waiwai i loko o ke kumu, loaʻa iā mākou C = 2π(7) = 14π iniha. Ma kahi o π i 3.14, hiki iā mākou ke helu i ke anapuni e like me 14(3.14) = 43.96 iniha. Hoʻopuni ʻia i ka ʻumi kokoke loa, ʻo 47.6 ʻīniha ke anapuni, pili i ka pane i hāʻawi ʻia.

Nīnau 8: He 10 mika ka radius o ka hapalua pōʻai. He aha kona ʻāpana?

A. 20 mika

B. 15 mika

C. 31.42 mika

D. 62.84 mika

✅ Pane Pololei:

C. 31.42 mika

Hōʻike:No ka huli ana i ke anapuni o ka hapalua poai, e helu i ka hapalua o ke anapuni o ka poai piha me ka radius o 10 mika.

hoʻohālike pōʻai — *Hoʻohālike pōʻai o ka pōʻai*

Nīnau 9: Pāʻani ka hui pōʻaleʻa me ke kinipōpō me ka radius o 5.6 iniha. He aha ke anapuni o kēlā me kēia pōpōpō?

A. 11.2 iniha

B. 17.6 iniha

C. 22.4 iniha

D. 35.2 iniha

✅ Pane Pololei:

C. 22.4 iniha

Hōʻike:

Hiki iā ʻoe ke hoʻohana i ke ʻano no ke anapuni o kahi pōʻai, ʻo ia hoʻi C = 2πr. ʻO ka radius i hāʻawi ʻia he 5.6 iniha. E hoʻopili i kēia waiwai i loko o ke kumu, loaʻa iā mākou C = 2π * 5.6 iniha. C ≈ 2 * 3.14 * 5.6 iniha. C ≈ 11.2 * 5.6 iniha. C ≈ 22.4 iniha. No laila, ma kahi o 22.4 iniha ke anapuni o kēlā me kēia pōpōpō. Hōʻike kēia i ka mamao a puni ka pōpōpō.

Nīnau 10: Ke kūkulu nei ʻo Sarah a me kāna mau hoa ʻelua i papaʻaina pōʻai pōʻai no ko lākou ʻākoakoa ʻana. Ua ʻike lākou i mea e noho ʻoluʻolu ai lākou a pau a puni ka pākaukau, pono lākou he 18 kapuaʻi ke anapuni. He aha ke anawaena e pono ai ka papaʻaina pīniki e loaʻa ai ke anapuni kūpono?

A. 3 kapuai

B. 6 kapuai

C. 9 kapuai

D. 12 kapuai

✅ Pane Pololei:

B. 6 kapuai

Hōʻike:

No ka huli ʻana i ka radius, e puʻunaue i ke anapuni me 2π, ua loaʻa iā mākou r = C / (2π) r = 18 kapuaʻi / (2 * 3.14) r ≈ 18 kapuaʻi / 6.28 r ≈ 2.87 kapuaʻi (hoʻopuni ʻia i ka haneli kokoke loa).

I kēia manawa, no ka huli ʻana i ke anawaena, e pāpālua wale i ka radius: Diameter = 2 * Anawaena ≈ 2 * 2.87 kapuai Anawaena ≈ 5.74 kapuai. No laila, he 5.74 kapuaʻi ke anawaena o ka pākaukau pīniki

ʻO nā lawe waiwai

AhaSlides ʻo ia ka mea hana kuʻikahi pāʻani maikaʻi loa e hiki ke hoʻohana ʻia ka pāpale no ka hoʻonaʻauao, hoʻomaʻamaʻa ʻana, a i ʻole nā mea leʻaleʻa. E nānā AhaSlides koke no ka noa hoʻopilikino ʻiaa me nā hiʻohiʻona holomua!

Pinepine ninau ninaninau 'ana i

He aha ka 2πr o ka pōʻai?

ʻO 2πr ke kumu no ke anapuni o ka pōʻai. Ma kēia ʻano kumu:

ʻO "2" e hōʻike ana e lawe ʻelua ʻoe i ka lōʻihi o ka radius. ʻO ke anapuni ka mamao a puni ka pōʻai, no laila pono ʻoe e hele a puni ka pōʻai i hoʻokahi manawa a laila hou, ʻo ia ke kumu e hoʻonui ai mākou i ka 2.
"π" (pi) he makemakika mau e like me 3.14159. Hoʻohana ʻia no ka mea e hōʻike ana i ka pilina ma waena o ke anapuni a me ke anawaena o kahi pōʻai.
ʻO ka "r" ka radius o ka pōʻai, ʻo ia ka mamao mai ke kikowaena o ka pōʻai a hiki i kekahi kiko ma kona ʻapoʻai.

No ke aha he 2πr ke anapuni?

ʻO ke kumu no ke anapuni o ka pōʻai, C = 2πr, mai ka wehewehe ʻana o pi (π) a me nā waiwai geometric o kahi pōʻai. Hōʻike ka Pi (π) i ka ratio o ke anapuni o ka pōʻai i kona anawaena. Ke hoʻonui ʻoe i ka radius (r) me ka 2π, e helu pono ʻoe i ka mamao a puni ka pōʻai, ʻo ia ka wehewehe o ke anapuni.

He 3.14 ka nui o ke anapuni i ka radius?

ʻAʻole, ʻaʻole pololei ka 3.14 manawa o ke anapuni. Hāʻawi ʻia ka pilina ma waena o ke anapuni a me ka radius o kahi pōʻai e ke kumu C = 2πr. ʻOiai ʻo π (pi) ma kahi o 3.14159, ʻo ke anapuni ʻo 2 manawa π manawa i ka radius. No laila, ʻoi aku ka nui o ke anapuni ma mua o 3.14 manawa i ka radius; he 2 manawa π manawa o ka radius.

Manaʻo Kōkua: ʻOmni Caculator | Ua haʻi aku ʻo Profof