10 Чөлөөт тойрог тойргийн асуулт хариултын дадлага хийх

Тойргийн тойргийг яг яаж тооцоолох вэ?

Тойргийн тойрог гэдэг нь бага, дунд сургуульд оруулах шаардлагатай математикийн суурь мэдлэг юм. Тойргийн тойргийг эзэмших нь ахлах сургууль, коллежид математикийн ахисан түвшний сургалтанд хамрагдаж, SAT, ACT зэрэг стандартчилсан шалгалтанд бэлтгэхээр төлөвлөж буй оюутнуудад зайлшгүй шаардлагатай.

Энэ нийтлэл дэх тойргийн 10 тойргийн асуулт хариулт нь тойргийн радиус, диаметр, тойргийг олох талаарх таны ойлголтыг шалгах зорилготой юм.

Гарчиг:

Тойргийн томъёоны тойрог
Тойргийн тойргийн асуулт хариулт
Түлхүүрийг авах
Түгээмэл асуултууд

Тойргийн томъёоны тойрог

Шалгалт өгөхөөс өмнө зарим чухал мэдээллийг тоймлон хэлье!

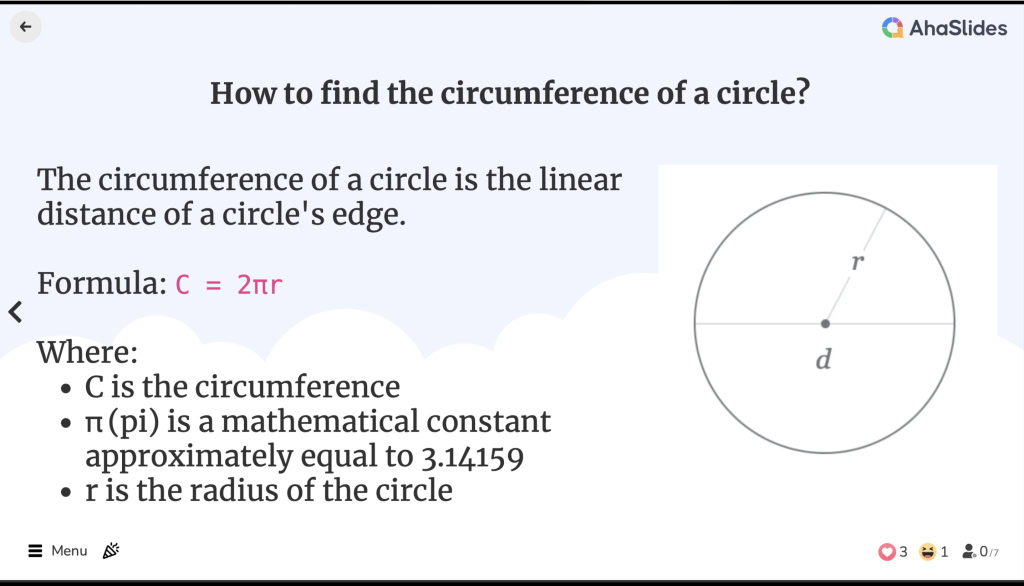
тойргийн тойргийг хэрхэн олох вэ — *Тойргийн тойргийг хэрхэн олох вэ*

Тойргийн тойрог хэд вэ?

Тойргийн тойрог нь тойргийн ирмэгийн шугаман зай юм. Энэ нь геометрийн хэлбэрийн периметртэй тэнцүү боловч периметр гэдэг нэр томъёо нь зөвхөн олон өнцөгтүүдэд ашиглагддаг.

Тойргийн тойргийг хэрхэн олох вэ?

Тойргийн тойргийн томъёо нь:

C = 2πr

хаана:

C нь тойрог юм
π (pi) нь ойролцоогоор 3.14159-тэй тэнцүү математикийн тогтмол юм
r нь тойргийн радиус юм

Радиус нь тойргийн төвөөс ирмэгийн аль ч цэг хүртэлх зай юм.

Диаметр нь радиусаас хоёр дахин их тул тойргийг дараах байдлаар илэрхийлж болно.

C = πd

хаана:

d нь диаметр

Жишээлбэл, тойргийн радиус 5 см бол тойрог нь:

C = 2πr = 2π * 5 cm = 10π cm

≈ 31.4 см (аравтын 2 орон хүртэл дугуйрсан)

Дэлгэрэнгүй зөвлөмжүүд AhaSlides

AhaSlides бол The Ultimate Quiz Maker юм

Уйтгарыг арилгахын тулд манай өргөн хүрээний загварын номын санг ашиглан интерактив тоглоомуудыг нэн даруй бүтээгээрэй

Асуулт асууж байгаа хүмүүс AhaSlides оролцооны намын санаануудын нэг юм — *Уйтгартай үедээ тоглох онлайн тоглоомууд*

ҮНЭГҮЙ БҮРТГЭЛ АВАХ

Тойргийн тойргийн асуулт хариулт

Асуулт 1: Дугуй хэлбэртэй усан бассейны тойрог 50 метр бол түүний радиус хэд вэ?

A. 7.95 метр

B. 8.00 метр

C. 15.91 метр

D. 25 метр

✅ Зөв хариулт:

A. 7.95 метр

Тайлбар:

Радиусыг C = 2πr томъёог дахин цэгцэлж, r: r = C / (2π) -ийг шийдэх замаар олж болно. Өгөгдсөн 50 метрийн тойргийг залгаад π-ийг 3.14-д ойртуулахад бид радиус нь ойролцоогоор 7.95 метр болно.

Асуулт 2: Тойргийн диаметр нь 14 инч. Түүний радиус хэд вэ?

A. 28 инч

B.14 инч

C. 21 инч

D. 7 инч

✅ Зөв хариулт:

D. 7 инч

Тайлбар:

Диаметр нь радиусын уртаас хоёр дахин их (d = 2r) тул та диаметрийг 2 (r = d / 2) хуваах замаар радиусыг олох боломжтой. Энэ тохиолдолд өгөгдсөн 14 инч диаметрийг 2-т хуваахад a гарна. радиус 7 инч.

тойргийн тойргийг ол — *Тойргийн тойргийг ол*

Асуулт 3: Тойргийн диаметр ба тойргийн хоорондын хамаарлын талаар дараах мэдэгдлүүдийн аль нь үнэн бэ?

A. Диаметр нь тойргийн хагас юм.

B. Диаметр нь тойрогтой ижил байна.

C. Диаметр нь тойргийн хэмжээнээс хоёр дахин их байна.

D. Диаметр нь тойргийг π үржүүлсэн байна.

✅ Зөв хариулт:

A. Диаметр нь тойргийн хагас юм.

Тайлбар:

Диаметр нь радиусаас 2 дахин их, тойрог нь 2π радиустай тэнцүү байна. Тиймээс диаметр нь тойргийн хагас юм.

Асуулт 4: Бидний суух ёстой ширээний тойрог нь 6.28 ярд. Бид хүснэгтийн диаметрийг олох хэрэгтэй.

A. 1 ярд

B. 2 ярд

C. 3 ярд

D. 4 ярд

✅ Зөв хариулт:

B. 2 ярд

Тайлбар:

Тойргийн тойргийг диаметрийг pi (π) -ээр үржүүлж тооцоолно. Энэ тохиолдолд тойргийг 6.28 ярд гэж заасан. Диаметрийг олохын тулд бид тойргийг пи-д хуваах хэрэгтэй. 6.28 ярдыг пи-д хуваахад ойролцоогоор 2 ярд болно. Тиймээс ширээний диаметр нь 2 метр байна.

Асуулт 5: Дугуй цэцэрлэг нь 36 метрийн тойрогтой. Цэцэрлэгийн ойролцоогоор радиус хэд вэ?

A. 3.14 метр

B. 6 метр

C. 9 метр

D. 18 метр

✅ Зөв хариулт:

C. 9 метр

Тайлбар:

Радиусыг олохын тулд тойргийн томъёог ашиглана: C = 2πr. Радиусыг шийдэхийн тулд томъёог дахин цэгцлээрэй: r = C / (2π). Өгөгдсөн тойргийн 36 метрийг залгаад π-ийн ойролцоо утгыг 3.14 гэж ашиглавал r = 36 / (2 * 3.14) ≈ 9 метр болно.

Асуулт 6: Дугуй хэлбэртэй усан бассейн нь 8 метрийн радиустай. Усан сэлэгч нэг тойрог хийхдээ цөөрмийн эргэн тойронд ойролцоогоор хэдэн зайг туулах вэ?

A. 16 метр

B. 25 метр

C. 50 метр

D. 100 метр

✅ Зөв хариулт:

C. 50 метр

Тайлбар:

Усанд сэлэгч нэг тойрогт усан санг тойрох зайг олохын тулд та тойргийн томьёог (C = 2πr) ашиглана. Энэ тохиолдолд энэ нь 2 * 3.14 * 8 метр ≈ 50.24 метр бөгөөд ойролцоогоор 50 метр юм.

Асуулт 7: Ангидаа хула цагирагыг хэмжихдээ C бүлгийнхэн 7 инч радиустай болохыг олж мэдэв. Хула цагирагны тойрог хэд вэ?

A. 39.6 инч

B. 37.6 инч

C. 47.6 инч

D. 49.6 инч

✅ Зөв хариулт:

C. 47.6 инч

Тайлбар:

Тойргийн тойргийг C = 2πr томъёог ашиглан олж болно, энд r нь тойргийн радиус юм. Энэ тохиолдолд хула цагирагны радиусыг 7 инч гэж өгсөн. Энэ утгыг томъёонд оруулаад бид C = 2π(7) = 14π инч авна. Ойролцоогоор π-ийг 3.14 болгож тойргийг 14(3.14) = 43.96 инч гэж тооцоолж болно. Аравны нэг хүртэл дугуйрсан тойрог нь 47.6 инч бөгөөд энэ нь өгөгдсөн хариулттай тохирч байна.

Асуулт 8: Хагас тойрог нь 10 метр радиустай. Түүний периметр хэд вэ?

A. 20 метр

B. 15 метр

C. 31.42 метр

D. 62.84 метр

✅ Зөв хариулт:

C. 31.42 метр

Тайлбар:Хагас тойргийн периметрийг олохын тулд 10 метрийн радиустай бүтэн тойргийн хагасыг тооцоол.

тойргийн тойргийн жишээ — *Тойргийн тойргийн жишээ*

Асуулт 9: Сагсан бөмбөгийн баг 5.6 инч радиустай бөмбөгөөр тоглодог. Сагсан бөмбөг бүрийн тойрог хэд вэ?

A. 11.2 инч

B. 17.6 инч

C. 22.4 инч

D. 35.2 инч

✅ Зөв хариулт:

C. 22.4 инч

Тайлбар:

Та тойргийн тойргийн томьёог ашиглаж болно, энэ нь C = 2πr. Өгөгдсөн радиус нь 5.6 инч байна. Энэ утгыг томьёо руу залгаад бид C = 2π * 5.6 инч байна. C ≈ 2 * 3.14 * 5.6 инч. C ≈ 11.2 * 5.6 инч. C ≈ 22.4 инч. Тиймээс сагсан бөмбөг бүрийн тойрог ойролцоогоор 22.4 инч байна. Энэ нь сагсан бөмбөгийн эргэн тойрон дахь зайг илэрхийлнэ.

Асуулт 10: Сара болон түүний хоёр найз цугларахдаа зориулж дугуй хэлбэртэй пикник ширээ барьж байв. Тэд бүгдээрээ ширээ тойрон тухтай суухын тулд 18 фут тойрог хэрэгтэй гэдгийг мэдэж байсан. Тойрог зөв болгохын тулд пикникийн ширээ ямар диаметртэй байх ёстой вэ?

A. 3 фут

B. 6 фут

C. 9 фут

D. 12 фут

✅ Зөв хариулт:

B. 6 фут

Тайлбар:

Радиусыг олохын тулд тойргийг 2π-д хуваавал бид r = C / (2π) r = 18 фут / (2 * 3.14) r ≈ 18 фут / 6.28 r ≈ 2.87 фут (зууны нэг хүртэл дугуйрсан) байна.

Одоо диаметрийг олохын тулд радиусыг хоёр дахин нэмэгдүүлээрэй: Диаметр = 2 * Радиус Диаметр ≈ 2 * 2.87 фут Диаметр ≈ 5.74 фут. Тиймээс пикникийн ширээ нь ойролцоогоор 5.74 фут диаметртэй байх ёстой

Түлхүүрийг авах

AhaSlides малгайг боловсрол, сургалт, зугаа цэнгэлийн зориулалтаар ашиглаж болох шилдэг интерактив асуулт хариултын програм юм. Шалгах AhaSlides нэн даруй үнэгүй авах тохируулах боломжтой загваруудболон дэвшилтэт функцууд!

Түгээмэл асуултууд

Тойргийн 2πr гэж юу вэ?

2πr нь тойргийн тойргийн томьёо юм. Энэ томъёонд:

"2" нь радиусын уртаас хоёр дахин уртыг авч байгааг илэрхийлнэ. Тойрог нь тойргийг тойрсон зай тул та тойргийг нэг удаа тойрох хэрэгтэй, тиймээс бид 2-оор үржүүлдэг.
"π" (pi) нь ойролцоогоор 3.14159-тэй тэнцүү математикийн тогтмол юм. Энэ нь тойргийн тойрог ба диаметрийн хоорондын хамаарлыг илэрхийлдэг тул ашигладаг.
"r" нь тойргийн радиусыг илэрхийлдэг бөгөөд энэ нь тойргийн төвөөс тойргийн аль ч цэг хүртэлх зай юм.

Яагаад тойрог 2πr байдаг вэ?

Тойргийн тойргийн томьёо C = 2πr нь pi (π) ба тойргийн геометрийн шинж чанарын тодорхойлолтоос гаралтай. Pi (π) нь тойргийн тойргийг түүний диаметртэй харьцуулсан харьцааг илэрхийлнэ. Хэрэв та радиусыг (r) 2π-ээр үржүүлбэл тойргийг тойрсон зайг үндсэндээ тооцдог бөгөөд энэ нь тойргийн тодорхойлолт юм.

Тойрог нь радиусаас 3.14 дахин их үү?

Үгүй ээ, тойрог нь радиусаас яг 3.14 дахин их биш юм. Тойргийн тойрог ба радиус хоорондын хамаарлыг C = 2πr томъёогоор тодорхойлно. π (pi) нь ойролцоогоор 3.14159 байхад тойрог нь радиусаас 2 дахин π үржсэн байна. Тиймээс тойрог нь радиусаас ердөө 3.14 дахин их байна; энэ нь радиусаас 2 дахин π үржсэн байна.

Ref: Omni тооцоолуур | Проф