10 Li'o fua ole su'ega li'o e fa'ata'ita'i | 2024 Fa'afouga

E fa'afefea ona fa'atatau tonu le Circumference o se li'o?

O le li'o o le li'o ose malamalama fa'atatau ma mana'omia ile numera fa'alauiloa ile aoga tulagalua po'o le tulaga lua. O le a'oa'oina o le li'o o le li'o e mana'omia mo tamaiti a'oga o lo'o fuafua e tulituliloa a'oa'oga o le matematika i le a'oga maualuga ma le kolisi ma sauni mo su'ega fa'ata'atia e pei ole SAT ma le ACT.

O le 10 Circumference of a Circle Quiz i lenei tusiga ua mamanuina e suʻe ai lou malamalama i le sailia o le radius, diameter, ma le liʻo o se liʻo.

Lisi o Mataupu:

Liʻo o se lio faʻatulaga
Li'o o se su'ega li'o
Auala autu
Fesili e Masani ona Fesiligia

Liʻo o se lio faʻatulaga

Aʻo leʻi faia se suʻega, seʻi o tatou toe faʻamatalaina ni faʻamatalaga taua!

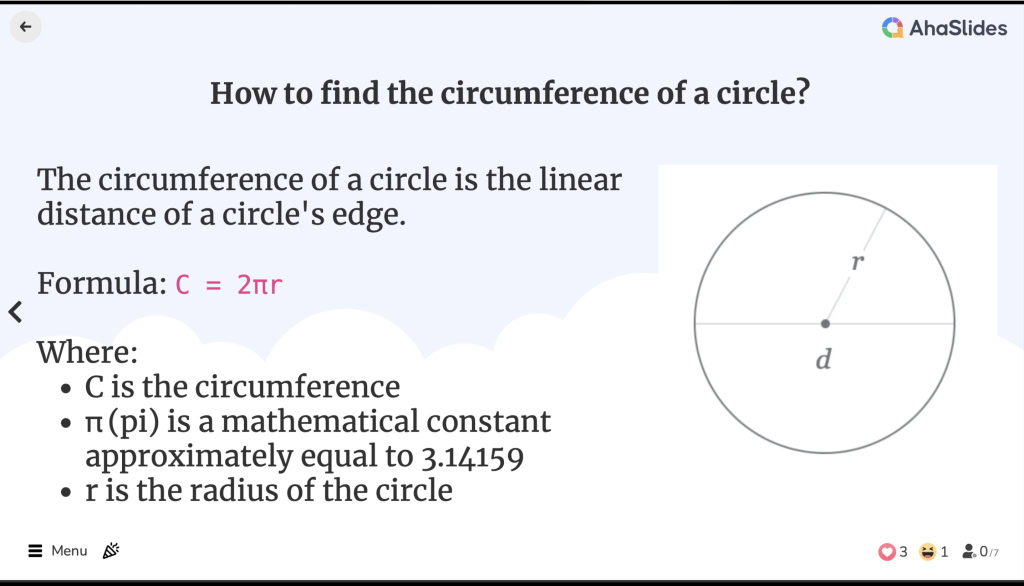
pe faapefea ona maua le faataamilosaga o se li'o — *Fa'afefea ona su'e le li'o o le li'o*

O le a le faataamilosaga o le li'o?

O le faataamilosaga o le li'o o le laina laina o le pito o le li'o. E tutusa ma le nofoaga o se foliga geometric, e ui o le faaupuga perimeter e naʻo le faʻaaogaina mo polygons.

E fa'afefea ona su'e le li'o o le li'o?

Ole fua ole li'o ole li'o ole:

C = 2πr

pe afai:

C o le faataamilosaga
π (pi) ose fa'a-matematika tumau e tusa ma le 3.14159
r o le alalaupapa o le li'o

O le radius o le mamao lea mai le ogatotonu o le li'o i so'o se itu i le pito.

O le lautele e faaluaina le radius, o lea e mafai foi ona faʻaalia le taamilosaga e pei o:

C = πd

pe afai:

d o le lautele

Mo se faʻataʻitaʻiga, afai o le radius o se liʻo e 5 cm, o lona uiga o le taamilosaga:

C = 2πr = 2π * 5 cm = 10π cm

≈ 31.4 cm (faataamilomilo i le 2 tesimale nofoaga)

Tele Fautuaga mai AhaSlides

AhaSlides o Le Fai Suega Sili

Fai ni ta'aloga fegalegaleai i se taimi fa'atasi ma la matou faletusi fa'ata'ita'i tele e tape ai le fiu

Tagata o lo'o ta'alo le su'ega AhaSlides e pei o se tasi o manatu o pati fa'aipoipo — *Taaloga i luga ole laiga e ta'alo pe a fiu*

GRAB FREE ACCOUNT

Li'o o se su'ega li'o

Fesili 1: Afai e 50 mita le ta'amilosaga o se vaita'ele li'o, o le a lona laina?

A. 7.95 mita

B. 8.00 mita

C. 15.91 mita

D. 25 mita

✅ Tali sa'o:

A. 7.95 mita

Faamatalaga:

E mafai ona maua le radius e ala i le toe fa'atulagaina o le fua fa'atatau C = 2πr ma fofo mo r: r = C / (2π). O le fa'apipi'iina o le li'o fa'atatau o le 50 mita ma fa'atatau i le π i le 3.14, matou te maua ai le radius e tusa ma le 7.95 mita.

Fesili 2: O le lautele ole li'o e 14 inisi. O le a lona alalaupapa?

A. 28 inisi

B.14 inisi

C. 21 inisi

D. 7 inisi

✅ Tali sa'o:

D. 7 inisi

Faamatalaga:

Talu ai ona e faaluaina le lautele o le umi o le radius (d = 2r), e mafai ona e mauaina le alalaupapa e ala i le vaevaeina o le lautele i le 2 (r = d / 2). I lenei tulaga, o le vaevaeina o le lautele o le 14 inisi i le 2 e maua ai se radius o 7 inisi.

saili le faataamilosaga o se li'o — *Su'e le faataamilosaga o se li'o*

Fesili 3: O le fea o fa'amatalaga nei e moni e uiga i le va o le lautele ma le faataamilosaga o le li'o?

A. O le lautele o le afa o le faataamilosaga.

B. O le lautele e tutusa ma le faataamilosaga.

C. O le lautele e faaluaina le faataamilosaga.

D. O le lautele o le π fa'alua i le li'o.

✅ Tali sa'o:

A. O le lautele o le afa o le faataamilosaga.

Faamatalaga:

O le lautele e tutusa ma le 2 taimi o le radius, ae o le faataamilosaga e tutusa ma le 2π taimi ole radius. O le mea lea, o le lautele o le afa o le taamilosaga.

Fesili 4: O le laulau tatou te nonofo ai e 6.28 iata le taamilosaga. Matou te manaʻomia le suʻeina o le lautele o le laulau.

A. 1 iata

B. 2 iata

C. 3 iata

D. 4 iata

✅ Tali sa'o:

B. 2 iata

Faamatalaga:

O le ta'amilosaga o le li'o e fa'atatauina e ala i le fa'ateleina o le lautele i le pi (π). I lenei tulaga, o le faataamilosaga o loʻo tuʻuina atu e 6.28 iata. Ina ia maua le lautele, tatou te manaʻomia le vaevaeina o le taamilosaga ile pi. O le vaevaeina o le 6.28 iata ile pi e maua ai pe tusa ma le 2 iata. O le mea lea, o le lautele o le laulau e 2 iata.

Fesili 5: O se togalaau lapotopoto e 36 mita lona faataamilosaga. O le a le fua faatatau o le togalaau?

A. 3.14 mita

B. 6 mita

C. 9 mita

D. 18 mita

✅ Tali sa'o:

C. 9 mita

Faamatalaga:

Ina ia su'e le radius, fa'aaoga le fua fa'atatau mo le li'o: C = 2πr. Toe fetu'una'i le fua fa'atatau e fo'ia ai le alalaupapa: r = C / (2π). O le fa'apipi'iina o le li'o fa'atatau o le 36 mita ma le fa'aogaina o le tau fa'atatau o le π e pei o le 3.14, e te maua le r = 36 / (2 * 3.14) ≈ 9 mita.

Fesili 6: Ole vaita'ele li'o e 8 mita lona lautele. O le a le mamao e fealua'i ai se tagata aau i le vaita'ele pe a uma le tasi vae?

A. 16 mita

B. 25 mita

C. 50 mita

D. 100 mita

✅ Tali sa'o:

C. 50 mita

Faamatalaga:

Ina ia su'e le mamao e fealua'i ai le tagata aau i le vaita'ele mo le vae tasi, e te fa'aogaina le fua fa'atatau (C = 2πr). I lenei tulaga, o le 2 * 3.14 * 8 mita ≈ 50.24 mita, lea e tusa ma le 50 mita.

Fesili 7: I le fuaina o le hula hula i le vasega, na iloa ai e le vaega C e 7 inisi lona lautele. O le a le taamilosaga o le hula hula?

A. 39.6 inisi

B. 37.6 inisi

C. 47.6 inisi

D. 49.6 inisi

✅ Tali sa'o:

C. 47.6 inisi

Faamatalaga:

E mafai ona maua le ta'amilosaga o le li'o e fa'aaoga ai le fua fa'atatau C = 2πr, lea o le r o le radius o le li'o. I lenei tulaga, o le radius o le hula hoop e tuʻuina atu e 7 inisi. O le fa'apipi'iina o lenei tau i le fua fa'atatau, e maua ai le C = 2π(7) = 14π inisi. Fa'atatau ile π ile 3.14, e mafai ona tatou fa'atatauina le ta'amilosaga e pei ole 14(3.14) = 43.96 inisi. Fa'ata'amilo i le sefulu lata ane, o le li'o o le 47.6 inisi, e fetaui ma le tali na tu'uina atu.

Fesili 8: O le afa li'o e 10 mita lona lautele. O le a lona nofoaga?

A. 20 mita

B. 15 mita

C. 31.42 mita

D. 62.84 mita

✅ Tali sa'o:

C. 31.42 mita

Faamatalaga:Ina ia su'e le pito o le afa li'o, fuafua le afa o le lio o le li'o atoa ma le 10 mita le umi.

faataamilosaga o se faataitaiga li'o — *Fa'ata'amilosaga o se fa'ata'ita'iga li'o*

Fesili 9: E ta'alo le 'au pasiketipolo i se polo e 5.6 inisi le lautele. O le a le taamilosaga o pasiketipolo taitasi?

A. 11.2 inisi

B. 17.6 inisi

C. 22.4 inisi

D. 35.2 inisi

✅ Tali sa'o:

C. 22.4 inisi

Faamalamalamaga:

E mafai ona e fa'aogaina le fua fa'atatau mo le li'o o le li'o, o le C = 2πr. Ole laina ole laina ole 5.6 inisi. Fa'apipi'i lenei tau i le fua fa'atatau, o lo'o iai le matou C = 2π * 5.6 inisi. C ≈ 2 * 3.14 * 5.6 inisi. C ≈ 11.2 * 5.6 inisi. C ≈ 22.4 inisi. O lea la, o le taamilosaga o pasiketipolo taitasi e tusa ma le 22.4 inisi. O lo'o fa'atusalia ai le mamao o le pasiketipolo.

Fesili 10: Sa fauina e Sara ma ana uo e toalua se laulau taamilo mo tafaoga mo la latou faatasiga. Na latou iloa ina ia mafai e i latou uma ona nonofo solo i le laulau, latou te manaʻomia se taamilosaga e 18 futu. O le a le lautele e tatau ona i ai i le laulau pikiniki e maua ai le faataamilosaga sa'o?

A. 3 futu

B. 6 futu

C. 9 futu

D. 12 futu

✅ Tali sa'o:

B. 6 futu

Faamatalaga:

Ina ia su'e le fuala'au, vaevae le ta'amilosaga i le 2π, e iai le r = C / (2π) r = 18 futu / (2 * 3.14) r ≈ 18 futu / 6.28 r ≈ 2.87 futu (fa'ata'amilosaga i le selau lata ane).

Ia, e su'e le ta'amilosaga, na'o le fa'aluaina o le radius: Diameter = 2 * Radius Diameter ≈ 2 * 2.87 feet Diameter ≈ 5.74 feet. O lea la, o le laulau pikiniki e tatau ona i ai le lautele e tusa ma le 5.74 futu

Auala autu

AhaSlides o le fai su'ega sili ona lelei feso'ota'iga e mafai ona fa'aoga pulou mo a'oa'oga, toleniga, po'o fa'afiafiaga. Siaki atu AhaSlides vave ona maua fua fa'ata'ita'iga fa'apitoama foliga sili atu!

Fesili e Masani ona Fesiligia

O le a le 2πr o le li'o?

2πr o le fua fa'atatau mo le li'o o le li'o. I lenei fua fa'atatau:

"2" o lo'o fa'atusalia e te fa'aluaina le umi o le radius. O le li'o o le mamao lea e ta'amilo ai le li'o, o lea e tatau ai ona e fa'ata'amilo i le li'o fa'atasi ma toe, o le mea lea tatou te fa'ateleina i le 2.
"π" (pi) ose fa'a-matematika tumau e tusa ma le 3.14159. E fa'aaogaina aua e fa'atusalia ai le va o le li'o ma le lautele o le li'o.
"r" o loʻo faʻatusalia ai le radius o le liʻo, o le mamao lea mai le ogatotonu o le liʻo i soʻo se itu i luga o lona liʻo.

Aisea e 2πr le faataamilosaga?

O le fua fa'atatau o le li'o o le li'o, C = 2πr, e sau mai le fa'auigaina o le pi (π) ma uiga fa'atusa o le li'o. Pi (π) o lo'o fa'atusalia le fua faatatau o le li'o o le li'o i lona lautele. A e fa'ateleina le radius (r) i le 2π, e te fa'atatauina le mamao o le li'o, o le fa'amatalaga lea o le li'o.

E 3.14 fa'aono le li'o o le radius?

Leai, o le li'o e le'o le 3.14 fa'apei le radius. O le sootaga i le va o le li'o ma le radius o se li'o o lo'o tu'uina mai i le fua fa'atatau C = 2πr. A'o π (pi) e tusa ma le 3.14159, o le ta'amilosaga e 2 taimi π fa'ata'amilosaga. O lea la, o le faataamilosaga e sili atu nai lo na o le 3.14 taimi o le radius; e 2 taimi π fa'aitaimi le radius.

Faʻamata: Omni Caculator | Na saunoa Prof Prof