কিভাবে একটি বৃত্তের পরিধি সঠিকভাবে গণনা করা যায়?
একটি বৃত্তের পরিধি হল প্রাথমিক বা মাধ্যমিক বিদ্যালয়ে প্রবর্তিত একটি মৌলিক এবং প্রয়োজনীয় গণিত জ্ঞান। একটি বৃত্তের পরিধি আয়ত্ত করা ছাত্রদের জন্য অত্যাবশ্যক যারা হাই স্কুল এবং কলেজে আরও উন্নত গণিত কোর্স করার পরিকল্পনা করে এবং SAT এবং ACT এর মতো মানসম্মত পরীক্ষার জন্য প্রস্তুতি নেয়।
এই নিবন্ধে একটি বৃত্তের কুইজের 10 পরিধিটি একটি বৃত্তের ব্যাসার্ধ, ব্যাস এবং পরিধি খোঁজার বিষয়ে আপনার বোঝার পরীক্ষা করার জন্য ডিজাইন করা হয়েছে।
সুচিপত্র:
একটি বৃত্ত সূত্রের পরিধি
Before taking a test, let's recap some crucial information!
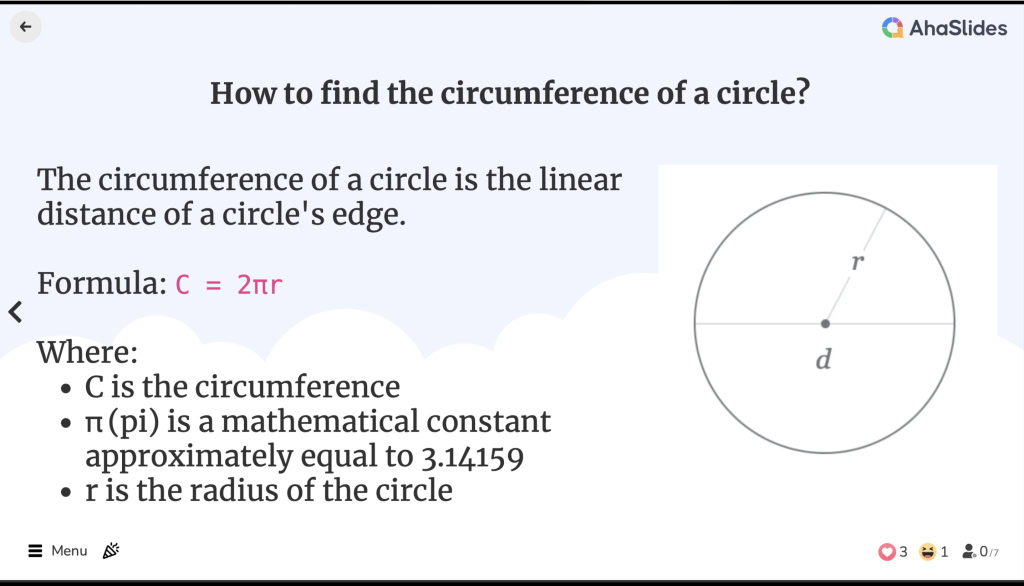
কিভাবে একটি বৃত্তের পরিধি খুঁজে বের করতে হয়একটি বৃত্তের পরিধি কত?
The circumference of a circle is the linear distance of a circle's edge. It is equivalent to the perimeter of a geometric shape, although the term perimeter is only used for polygons.
কিভাবে একটি বৃত্তের পরিধি খুঁজে বের করতে হয়?
একটি বৃত্ত সূত্রের পরিধি হল:
C = 2πr
কোথায়:
- C হল পরিধি
- π (pi) হল একটি গাণিতিক ধ্রুবক যা প্রায় 3.14159 এর সমান
- r হল বৃত্তের ব্যাসার্ধ
ব্যাসার্ধ হল বৃত্তের কেন্দ্র থেকে প্রান্তের যেকোনো বিন্দুর দূরত্ব।
ব্যাস ব্যাসার্ধের দ্বিগুণ, তাই পরিধিকে এভাবে প্রকাশ করা যেতে পারে:
C = πd
কোথায়:
- d হল ব্যাস
উদাহরণস্বরূপ, যদি একটি বৃত্তের ব্যাসার্ধ 5 সেমি হয়, তাহলে পরিধি হল:
C = 2πr = 2π * 5 cm = 10π cm
≈ 31.4 সেমি (2 দশমিক স্থানে বৃত্তাকার)
আহস্লাইডস থেকে আরও টিপস
- ক্লাসে মজাদার অনুশীলনের জন্য 70+ গণিত কুইজ প্রশ্ন
- বিরক্ত K10 ছাত্রদের জন্য 12টি সেরা শ্রেণীকক্ষ গণিত গেম
- প্রাপ্তবয়স্কদের জন্য ব্রেন টিজারের 60টি দুর্দান্ত ধারণা | 2023 আপডেট
AhaSlides হল চূড়ান্ত কুইজ মেকার
একঘেয়েমি মারতে আমাদের বিস্তৃত টেমপ্লেট লাইব্রেরির সাথে তাত্ক্ষণিকভাবে ইন্টারেক্টিভ গেম তৈরি করুন
বিরক্ত হলে অনলাইন গেম খেলতে হবেএকটি বৃত্ত কুইজের পরিধি
প্রশ্ন 1: একটি বৃত্তাকার সুইমিং পুলের পরিধি 50 মিটার হলে, এর ব্যাসার্ধ কত?
উঃ 7.95 মিটার
B. 8.00 মিটার
গ. 15.91 মিটার
D. 25 মিটার
✅ সঠিক উত্তর:
উঃ 7.95 মিটার
ব্যাখ্যা:
C = 2πr সূত্রটি পুনর্বিন্যাস করে এবং r: r = C / (2π) এর সমাধান করে ব্যাসার্ধটি পাওয়া যেতে পারে। 50 মিটার এবং আনুমানিক π থেকে 3.14 এর প্রদত্ত পরিধিতে প্লাগিং করলে, আমরা পাই ব্যাসার্ধটি প্রায় 7.95 মিটার।
প্রশ্ন 2: একটি বৃত্তের ব্যাস 14 ইঞ্চি। এর ব্যাসার্ধ কত?
উঃ ২৮ ইঞ্চি
B.14 ইঞ্চি
গ. 21 ইঞ্চি
D. 7 ইঞ্চি
✅ সঠিক উত্তর:
D. 7 ইঞ্চি
ব্যাখ্যা:
যেহেতু ব্যাসটি ব্যাসার্ধের দৈর্ঘ্যের দ্বিগুণ (d = 2r), আপনি ব্যাসার্ধটিকে 2 (r = d / 2) দ্বারা ভাগ করে ব্যাসার্ধ খুঁজে পেতে পারেন। এই ক্ষেত্রে, প্রদত্ত 14 ইঞ্চি ব্যাসকে 2 দ্বারা ভাগ করলে a পাওয়া যায়। 7 ইঞ্চি ব্যাসার্ধ।
একটি বৃত্তের পরিধি নির্ণয় করপ্রশ্ন 3: বৃত্তের ব্যাস এবং পরিধির মধ্যে সম্পর্ক সম্পর্কে নিচের কোন বিবৃতিটি সত্য?
উ: ব্যাস হল পরিধির অর্ধেক।
B. ব্যাস পরিধির সমান।
C. ব্যাস পরিধির দ্বিগুণ।
D. ব্যাস হল পরিধির π গুণ।
✅ সঠিক উত্তর:
উ: ব্যাস হল পরিধির অর্ধেক।
ব্যাখ্যা:
ব্যাসটি ব্যাসার্ধের 2 গুণের সমান, যখন পরিধিটি ব্যাসার্ধের 2π গুণের সমান। অতএব, ব্যাস হল পরিধির অর্ধেক।
প্রশ্ন 4: আমাদের যে টেবিলে বসতে হবে তার পরিধি 6.28 গজ। আমাদের টেবিলের ব্যাস খুঁজে বের করতে হবে।
উ: 1 গজ
B. 2 গজ
গ. 3 গজ
D. 4 গজ
✅ সঠিক উত্তর:
B. 2 গজ
ব্যাখ্যা:
পাই (π) দ্বারা ব্যাস গুণ করে একটি বৃত্তের পরিধি গণনা করা হয়। এই ক্ষেত্রে, পরিধি 6.28 গজ হিসাবে দেওয়া হয়। ব্যাস খুঁজে পেতে, আমাদের পরিধিকে পাই দ্বারা ভাগ করতে হবে। পাই দ্বারা 6.28 গজ ভাগ করলে আমাদের প্রায় 2 গজ পাওয়া যায়। অতএব, টেবিলের ব্যাস 2 গজ।
প্রশ্ন 5: একটি বৃত্তাকার বাগানের পরিধি 36 মিটার। বাগানের আনুমানিক ব্যাসার্ধ কত?
উঃ 3.14 মিটার
B. 6 মিটার
গ. 9 মিটার
D. 18 মিটার
✅ সঠিক উত্তর:
গ. 9 মিটার
ব্যাখ্যা:
ব্যাসার্ধ খুঁজে বের করতে, পরিধির সূত্রটি ব্যবহার করুন: C = 2πr। ব্যাসার্ধের সমাধান করার জন্য সূত্রটি পুনরায় সাজান: r = C / (2π)। 36 মিটারের প্রদত্ত পরিধিতে প্লাগ করা এবং π এর আনুমানিক মান 3.14 হিসাবে ব্যবহার করলে, আপনি r = 36 / (2 * 3.14) ≈ 9 মিটার পাবেন।
প্রশ্ন 6: একটি বৃত্তাকার সুইমিং পুলের ব্যাসার্ধ 8 মিটার। একটি ল্যাপ শেষ করার সময় একজন সাঁতারু পুলের চারপাশে ভ্রমণের আনুমানিক দূরত্ব কত?
উঃ 16 মিটার
B. 25 মিটার
গ. 50 মিটার
D. 100 মিটার
✅ সঠিক উত্তর:
গ. 50 মিটার
ব্যাখ্যা:
To find the distance a swimmer travels around the pool for one lap, you use the circumference formula (C = 2πr). In this case, it's 2 * 3.14 * 8 meters ≈ 50.24 meters, which is approximately 50 meters.
প্রশ্ন 7: ক্লাসে হুলা হুপ পরিমাপ করার সময়, গ্রুপ সি আবিষ্কার করেছিল যে এটির ব্যাসার্ধ 7 ইঞ্চি ছিল। হুলা হুপের পরিধি কত?
উঃ ২৮ ইঞ্চি
খ. 37.6 ইঞ্চি
গ. 47.6 ইঞ্চি
D. 49.6 ইঞ্চি
✅ সঠিক উত্তর:
গ. 47.6 ইঞ্চি
ব্যাখ্যা:
C = 2πr সূত্র ব্যবহার করে একটি বৃত্তের পরিধি পাওয়া যাবে, যেখানে r হল বৃত্তের ব্যাসার্ধ। এই ক্ষেত্রে, হুলা হুপের ব্যাসার্ধ 7 ইঞ্চি হিসাবে দেওয়া হয়। এই মানটিকে সূত্রে প্লাগ করলে, আমরা C = 2π(7) = 14π ইঞ্চি পাই। আনুমানিক π থেকে 3.14, আমরা পরিধিটি 14(3.14) = 43.96 ইঞ্চি হিসাবে গণনা করতে পারি। নিকটতম দশম পর্যন্ত বৃত্তাকার, পরিধি হল 47.6 ইঞ্চি, যা প্রদত্ত উত্তরের সাথে মেলে।
প্রশ্ন 8: একটি অর্ধবৃত্তের ব্যাসার্ধ 10 মিটার। এর পরিধি কত?
উঃ 20 মিটার
B. 15 মিটার
গ. 31.42 মিটার
D. 62.84 মিটার
✅ সঠিক উত্তর:
গ. 31.42 মিটার
ব্যাখ্যা:অর্ধবৃত্তের পরিধি খুঁজে পেতে, 10 মিটার ব্যাসার্ধ সহ একটি পূর্ণ বৃত্তের অর্ধেক পরিধি গণনা করুন।
একটি বৃত্তের উদাহরণের পরিধিপ্রশ্ন 9: বাস্কেটবল দল 5.6 ইঞ্চি ব্যাসার্ধের একটি বল নিয়ে খেলে। প্রতিটি বাস্কেটবলের পরিধি কত?
উঃ ২৮ ইঞ্চি
খ. 17.6 ইঞ্চি
গ. 22.4 ইঞ্চি
D. 35.2 ইঞ্চি
✅ সঠিক উত্তর:
গ. 22.4 ইঞ্চি
ব্যাখ্যা:
আপনি একটি বৃত্তের পরিধির জন্য সূত্রটি ব্যবহার করতে পারেন, যা হল C = 2πr। প্রদত্ত ব্যাসার্ধ 5.6 ইঞ্চি। এই মানটিকে সূত্রে প্লাগ করুন, আমাদের কাছে C = 2π * 5.6 ইঞ্চি আছে। C ≈ 2 * 3.14 * 5.6 ইঞ্চি। C ≈ 11.2 * 5.6 ইঞ্চি। C ≈ 22.4 ইঞ্চি। সুতরাং, প্রতিটি বাস্কেটবলের পরিধি প্রায় 22.4 ইঞ্চি। এটি বাস্কেটবলের চারপাশের দূরত্বকে প্রতিনিধিত্ব করে।
প্রশ্ন 10: সারা এবং তার দুই বন্ধু তাদের জমায়েতের জন্য একটি বৃত্তাকার পিকনিক টেবিল তৈরি করছিল। তারা জানত যে তাদের সকলের আরামে টেবিলের চারপাশে বসার জন্য তাদের 18 ফুট পরিধি প্রয়োজন। সঠিক পরিধি অর্জন করতে পিকনিক টেবিলের কি ব্যাস থাকতে হবে?
উ: 3 ফুট
খ. 6 ফুট
গ. 9 ফুট
D. 12 ফুট
✅ সঠিক উত্তর:
খ. 6 ফুট
ব্যাখ্যা:
ব্যাসার্ধ খুঁজে বের করতে, পরিধিকে 2π দ্বারা ভাগ করুন, আমাদের আছে r = C / (2π) r = 18 ফুট / (2 * 3.14) r ≈ 18 ফুট / 6.28 r ≈ 2.87 ফুট (নিকটতম শততম পর্যন্ত বৃত্তাকার)।
এখন, ব্যাস খুঁজে বের করতে, ব্যাসার্ধের দ্বিগুণ করুন: ব্যাস = 2 * ব্যাসার্ধ ব্যাস ≈ 2 * 2.87 ফুট ব্যাস ≈ 5.74 ফুট। সুতরাং, পিকনিক টেবিলের ব্যাস হতে হবে প্রায় 5.74 ফুট
কী টেকওয়েস
অহস্লাইডস সেরা ইন্টারেক্টিভ কুইজ প্রস্তুতকারক যে টুপি শিক্ষা, প্রশিক্ষণ, বা বিনোদনের উদ্দেশ্যে ব্যবহার করা যেতে পারে। বিনামূল্যে পেতে অবিলম্বে AhaSlides দেখুন কাস্টমাইজযোগ্য টেমপ্লেটএবং উন্নত বৈশিষ্ট্য!
সচরাচর জিজ্ঞাস্য
একটি বৃত্তের 2πr কত?
2πr হল একটি বৃত্তের পরিধির সূত্র। এই সূত্রে:
- "2" represents that you are taking twice the length of the radius. The circumference is the distance around the circle, so you need to go around the circle once and then again, which is why we multiply by 2.
- "π" (pi) is a mathematical constant approximately equal to 3.14159. It's used because it represents the relationship between the circumference and the diameter of a circle.
- "r" represents the radius of the circle, which is the distance from the center of the circle to any point on its circumference.
পরিধি 2πr কেন?
একটি বৃত্তের পরিধির সূত্র, C = 2πr, পাই (π) এর সংজ্ঞা এবং একটি বৃত্তের জ্যামিতিক বৈশিষ্ট্য থেকে এসেছে। পাই (π) একটি বৃত্তের পরিধি এবং তার ব্যাসের অনুপাতকে উপস্থাপন করে। যখন আপনি ব্যাসার্ধ (r) কে 2π দ্বারা গুণ করেন, আপনি মূলত বৃত্তের চারপাশের দূরত্ব গণনা করেন, যা পরিধির সংজ্ঞা।
পরিধি কি ব্যাসার্ধের 3.14 গুণ?
No, the circumference is not exactly 3.14 times the radius. The relationship between the circumference and the radius of a circle is given by the formula C = 2πr. While π (pi) is approximately 3.14159, the circumference is 2 times π times the radius. So, the circumference is more than just 3.14 times the radius; it's 2 times π times the radius.
সুত্র: ওমনি ক্যাকুলেটর | Prof
ট্যাগ্স: কুইজ আইডিয়া
