10 Test de circumferència lliure d'un cercle per practicar

Com calcular exactament la circumferència d'un cercle?

La circumferència d'un cercle és un coneixement bàsic i obligatori de matemàtiques introduït a l'escola primària o secundària. Dominar la circumferència d'un cercle és essencial per als estudiants que planegen cursar cursos de matemàtiques més avançats a l'escola secundària i la universitat i preparar-se per a exàmens estandarditzats com el SAT i l'ACT.

El qüestionari de 10 circumferències d'un cercle d'aquest article està dissenyat per provar la vostra comprensió de trobar el radi, el diàmetre i la circumferència d'un cercle.

Taula de continguts:

Circumferència d’una fórmula de cercle
Circumferència d'un qüestionari de cercle
Transport per emportar claus
Preguntes freqüents

Circumferència d’una fórmula de cercle

Abans de fer una prova, resumim algunes dades crucials!

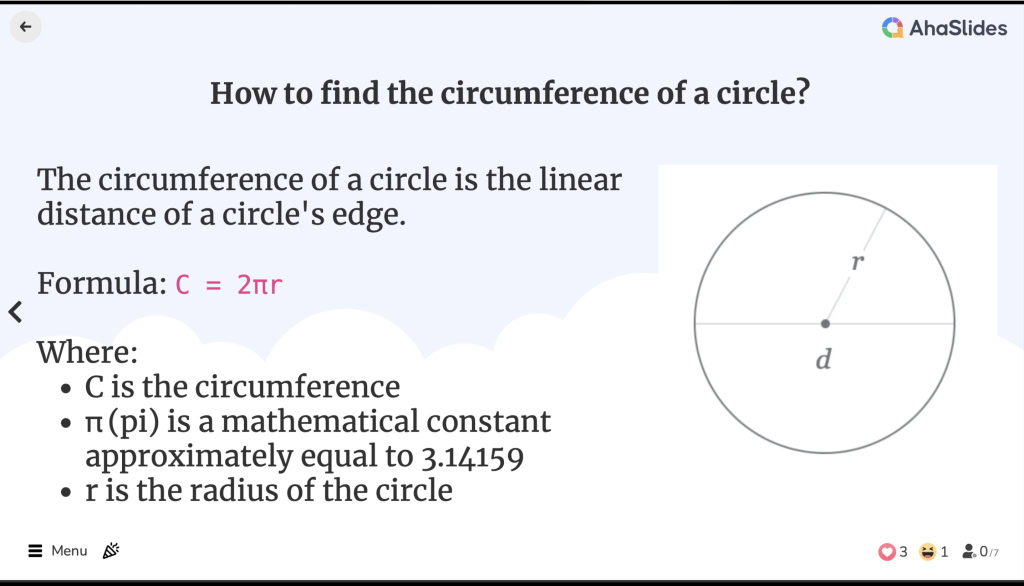
com trobar la circumferència d'un cercle — *Com trobar la circumferència d'un cercle*

Quina és la circumferència d'un cercle?

La circumferència d'un cercle és la distància lineal de la vora d'un cercle. És equivalent al perímetre d'una forma geomètrica, encara que el terme perímetre només s'utilitza per als polígons.

Com trobar la circumferència d'un cercle?

La fórmula de la circumferència d'un cercle és:

C = 2πr

on:

C és la circumferència
π (pi) és una constant matemàtica aproximadament igual a 3.14159
r és el radi de la circumferència

El radi és la distància des del centre del cercle fins a qualsevol punt de la vora.

El diàmetre és el doble del radi, de manera que la circumferència també es pot expressar com:

C = πd

on:

d és el diàmetre

Per exemple, si el radi d'un cercle és de 5 cm, aleshores la circumferència és:

C = 2πr = 2π * 5 cm = 10π cm

≈ 31.4 cm (arrodonit a 2 decimals)

Més consells de AhaSlides

AhaSlides és el millor creador de preguntes

Feu jocs interactius en un instant amb la nostra àmplia biblioteca de plantilles per matar l'avorriment

Gent jugant al qüestionari AhaSlides com una de les idees de festa de compromís — *Jocs en línia per jugar quan estàs avorrit*

AGRA UN COMPTE GRATIS

Circumferència d'un qüestionari de cercle

Pregunta 1: Si la circumferència d'una piscina circular és de 50 metres, quin és el seu radi?

A. 7.95 metres

B. 8.00 metres

C. 15.91 metres

D. 25 metres

✅ Resposta correcta:

A. 7.95 metres

Explicació:

El radi es pot trobar reordenant la fórmula C = 2πr i resolent per r: r = C / (2π). Connectant la circumferència donada de 50 metres i aproximant π a 3.14, trobem que el radi és d'aproximadament 7.95 metres.

Pregunta 2: el diàmetre d'un cercle és de 14 polzades. Quin és el seu radi?

A. 28 polzades

B.14 polzades

C. 21 polzades

D. 7 polzades

✅ Resposta correcta:

D. 7 polzades

Explicació:

Com que el diàmetre és el doble de la longitud del radi (d = 2r), podeu trobar el radi dividint el diàmetre per 2 (r = d / 2). radi de 14 polzades.

trobar la circumferència d'un cercle — *Troba la circumferència d'un cercle*

Pregunta 3: Quina de les següents afirmacions és certa sobre la relació entre el diàmetre i la circumferència d'un cercle?

A. El diàmetre és la meitat de la circumferència.

B. El diàmetre és el mateix que la circumferència.

C. El diàmetre és el doble de la circumferència.

D. El diàmetre és π vegades la circumferència.

✅ Resposta correcta:

A. El diàmetre és la meitat de la circumferència.

Explicació:

El diàmetre és igual a 2 vegades el radi, mentre que la circumferència és igual a 2π vegades el radi. Per tant, el diàmetre és la meitat de la circumferència.

Pregunta 4: La taula on ens hem de seure té una circumferència de 6.28 iardes. Hem de trobar el diàmetre de la taula.

A. 1 iarda

B. 2 iardes

C. 3 iardes

D. 4 iardes

✅ Resposta correcta:

B. 2 iardes

Explicació:

La circumferència d'un cercle es calcula multiplicant el diàmetre per pi (π). En aquest cas, la circumferència es dóna com a 6.28 iardes. Per trobar el diàmetre, hem de dividir la circumferència per pi. Dividir 6.28 iardes per pi ens dóna aproximadament 2 iardes. Per tant, el diàmetre de la taula és de 2 iardes.

Pregunta 5: Un jardí circular té una circumferència de 36 metres. Quin és el radi aproximat del jardí?

A. 3.14 metres

B. 6 metres

C. 9 metres

D. 18 metres

✅ Resposta correcta:

C. 9 metres

Explicació:

Per trobar el radi, utilitzeu la fórmula per a la circumferència: C = 2πr. Reordena la fórmula per resoldre el radi: r = C / (2π). Connectant la circumferència donada de 36 metres i utilitzant un valor aproximat de π com a 3.14, s'obté r = 36 / (2 * 3.14) ≈ 9 metres.

Pregunta 6: Una piscina circular té un radi de 8 metres. Quina és la distància aproximada que recorre un nedador al voltant de la piscina quan fa una volta?

A. 16 metres

B. 25 metres

C. 50 metres

D. 100 metres

✅ Resposta correcta:

C. 50 metres

Explicació:

Per trobar la distància que recorre un nedador al voltant de la piscina durant una volta, feu servir la fórmula de la circumferència (C = 2πr). En aquest cas, són 2 * 3.14 * 8 metres ≈ 50.24 metres, que són aproximadament 50 metres.

Pregunta 7: En mesurar el hula hoop a classe, el grup C va descobrir que tenia un radi de 7 polzades. Quina és la circumferència del hula hoop?

A. 39.6 polzades

B. 37.6 polzades

C. 47.6 polzades

D. 49.6 polzades

✅ Resposta correcta:

C. 47.6 polzades

Explicació:

La circumferència d'un cercle es pot trobar mitjançant la fórmula C = 2πr, on r és el radi del cercle. En aquest cas, el radi del hula hoop es dóna com a 7 polzades. Connectant aquest valor a la fórmula, obtenim C = 2π(7) = 14π polzades. Aproximant π a 3.14, podem calcular la circumferència com 14(3.14) = 43.96 polzades. Arrodonit a la dècima més propera, la circumferència és de 47.6 polzades, que coincideix amb la resposta donada.

Pregunta 8: Un semicercle té un radi de 10 metres. Quin és el seu perímetre?

A. 20 metres

B. 15 metres

C. 31.42 metres

D. 62.84 metres

✅ Resposta correcta:

C. 31.42 metres

Explicació:Per trobar el perímetre del semicercle, calcula la meitat de la circumferència d'un cercle complet amb un radi de 10 metres.

Pregunta 9: L'equip de bàsquet juga amb una pilota amb un radi de 5.6 polzades. Quina és la circumferència de cada pilota de bàsquet?

A. 11.2 polzades

B. 17.6 polzades

C. 22.4 polzades

D. 35.2 polzades

✅ Resposta correcta:

C. 22.4 polzades

Explicació:

Podeu utilitzar la fórmula per a la circumferència d'un cercle, que és C = 2πr. El radi donat és de 5.6 polzades. Connecteu aquest valor a la fórmula, tenim C = 2π * 5.6 polzades. C ≈ 2 * 3.14 * 5.6 polzades. C ≈ 11.2 * 5.6 polzades. C ≈ 22.4 polzades. Per tant, la circumferència de cada pilota de bàsquet és d'aproximadament 22.4 polzades. Això representa la distància al voltant de la pilota de bàsquet.

Pregunta 10: La Sarah i els seus dos amics estaven construint una taula de pícnic circular per a la seva reunió. Sabien que, per asseure'ls còmodament al voltant de la taula, necessitaven una circumferència de 18 peus. Quin diàmetre ha de tenir la taula de pícnic per aconseguir la circumferència correcta?

A. 3 peus

B. 6 peus

C. 9 peus

D. 12 peus

✅ Resposta correcta:

B. 6 peus

Explicació:

Per trobar el radi, dividiu la circumferència per 2π, tenim r = C / (2π) r = 18 peus / (2 * 3.14) r ≈ 18 peus / 6.28 r ≈ 2.87 peus (arrodonit a la centèsima més propera).

Ara, per trobar el diàmetre, simplement doble el radi: Diàmetre = 2 * Radi Diàmetre ≈ 2 * 2.87 peus Diàmetre ≈ 5.74 peus. Per tant, la taula de pícnic ha de tenir un diàmetre d'aproximadament 5.74 peus

Transport per emportar claus

AhaSlides és el millor fabricant de qüestionaris interactius que es pot utilitzar amb finalitats educatives, formatives o d'entreteniment. Fes una ullada AhaSlides de seguida per ser lliure plantilles personalitzablesi funcions avançades!

Preguntes freqüents

Què és 2πr d'una circumferència?

2πr és la fórmula per a la circumferència d'un cercle. En aquesta fórmula:

"2" representa que està prenent el doble de la longitud del radi. La circumferència és la distància al voltant del cercle, de manera que heu de fer una volta al cercle una i altra vegada, per això multipliquem per 2.
"π" (pi) és una constant matemàtica aproximadament igual a 3.14159. S'utilitza perquè representa la relació entre la circumferència i el diàmetre d'un cercle.
"r" representa el radi del cercle, que és la distància des del centre del cercle fins a qualsevol punt de la seva circumferència.

Per què la circumferència és 2πr?

La fórmula per a la circumferència d'un cercle, C = 2πr, prové de la definició de pi (π) i de les propietats geomètriques d'un cercle. Pi (π) representa la relació entre la circumferència d'un cercle i el seu diàmetre. Quan multipliqueu el radi (r) per 2π, es calcula essencialment la distància al voltant del cercle, que és la definició de circumferència.

La circumferència és 3.14 vegades el radi?

No, la circumferència no és exactament 3.14 vegades el radi. La relació entre la circumferència i el radi d'un cercle ve donada per la fórmula C = 2πr. Mentre que π (pi) és aproximadament 3.14159, la circumferència és 2 vegades π vegades el radi. Per tant, la circumferència és més que només 3.14 vegades el radi; és 2 vegades π vegades el radi.

Ref: Omni Caculator | Proprof