![]() ವೃತ್ತದ ಸುತ್ತಳತೆಯನ್ನು ನಿಖರವಾಗಿ ಲೆಕ್ಕಾಚಾರ ಮಾಡುವುದು ಹೇಗೆ?
ವೃತ್ತದ ಸುತ್ತಳತೆಯನ್ನು ನಿಖರವಾಗಿ ಲೆಕ್ಕಾಚಾರ ಮಾಡುವುದು ಹೇಗೆ?
![]() ವೃತ್ತದ ಸುತ್ತಳತೆಯು ಪ್ರಾಥಮಿಕ ಅಥವಾ ಮಧ್ಯಮ ಶಾಲೆಯಲ್ಲಿ ಪರಿಚಯಿಸಲಾದ ಮೂಲಭೂತ ಮತ್ತು ಅಗತ್ಯವಾದ ಗಣಿತ ಜ್ಞಾನವಾಗಿದೆ. ಪ್ರೌಢಶಾಲೆ ಮತ್ತು ಕಾಲೇಜಿನಲ್ಲಿ ಹೆಚ್ಚು ಸುಧಾರಿತ ಗಣಿತ ಕೋರ್ಸ್ಗಳನ್ನು ಮುಂದುವರಿಸಲು ಮತ್ತು SAT ಮತ್ತು ACT ನಂತಹ ಪ್ರಮಾಣಿತ ಪರೀಕ್ಷೆಗಳಿಗೆ ತಯಾರಿ ಮಾಡಲು ಯೋಜಿಸುವ ವಿದ್ಯಾರ್ಥಿಗಳಿಗೆ ವೃತ್ತದ ಸುತ್ತಳತೆಯನ್ನು ಮಾಸ್ಟರಿಂಗ್ ಮಾಡುವುದು ಅತ್ಯಗತ್ಯ.
ವೃತ್ತದ ಸುತ್ತಳತೆಯು ಪ್ರಾಥಮಿಕ ಅಥವಾ ಮಧ್ಯಮ ಶಾಲೆಯಲ್ಲಿ ಪರಿಚಯಿಸಲಾದ ಮೂಲಭೂತ ಮತ್ತು ಅಗತ್ಯವಾದ ಗಣಿತ ಜ್ಞಾನವಾಗಿದೆ. ಪ್ರೌಢಶಾಲೆ ಮತ್ತು ಕಾಲೇಜಿನಲ್ಲಿ ಹೆಚ್ಚು ಸುಧಾರಿತ ಗಣಿತ ಕೋರ್ಸ್ಗಳನ್ನು ಮುಂದುವರಿಸಲು ಮತ್ತು SAT ಮತ್ತು ACT ನಂತಹ ಪ್ರಮಾಣಿತ ಪರೀಕ್ಷೆಗಳಿಗೆ ತಯಾರಿ ಮಾಡಲು ಯೋಜಿಸುವ ವಿದ್ಯಾರ್ಥಿಗಳಿಗೆ ವೃತ್ತದ ಸುತ್ತಳತೆಯನ್ನು ಮಾಸ್ಟರಿಂಗ್ ಮಾಡುವುದು ಅತ್ಯಗತ್ಯ.
![]() ಈ ಲೇಖನದಲ್ಲಿ ವೃತ್ತದ ರಸಪ್ರಶ್ನೆಯ 10 ಸುತ್ತಳತೆ ವೃತ್ತದ ತ್ರಿಜ್ಯ, ವ್ಯಾಸ ಮತ್ತು ಸುತ್ತಳತೆಯನ್ನು ಕಂಡುಹಿಡಿಯುವ ನಿಮ್ಮ ತಿಳುವಳಿಕೆಯನ್ನು ಪರೀಕ್ಷಿಸಲು ವಿನ್ಯಾಸಗೊಳಿಸಲಾಗಿದೆ.
ಈ ಲೇಖನದಲ್ಲಿ ವೃತ್ತದ ರಸಪ್ರಶ್ನೆಯ 10 ಸುತ್ತಳತೆ ವೃತ್ತದ ತ್ರಿಜ್ಯ, ವ್ಯಾಸ ಮತ್ತು ಸುತ್ತಳತೆಯನ್ನು ಕಂಡುಹಿಡಿಯುವ ನಿಮ್ಮ ತಿಳುವಳಿಕೆಯನ್ನು ಪರೀಕ್ಷಿಸಲು ವಿನ್ಯಾಸಗೊಳಿಸಲಾಗಿದೆ.
![]() ಪರಿವಿಡಿ:
ಪರಿವಿಡಿ:
 ವೃತ್ತದ ಸೂತ್ರದ ಸುತ್ತಳತೆ
ವೃತ್ತದ ಸೂತ್ರದ ಸುತ್ತಳತೆ
![]() ಪರೀಕ್ಷೆಯನ್ನು ತೆಗೆದುಕೊಳ್ಳುವ ಮೊದಲು, ಕೆಲವು ನಿರ್ಣಾಯಕ ಮಾಹಿತಿಯನ್ನು ರೀಕ್ಯಾಪ್ ಮಾಡೋಣ!
ಪರೀಕ್ಷೆಯನ್ನು ತೆಗೆದುಕೊಳ್ಳುವ ಮೊದಲು, ಕೆಲವು ನಿರ್ಣಾಯಕ ಮಾಹಿತಿಯನ್ನು ರೀಕ್ಯಾಪ್ ಮಾಡೋಣ!
 ವೃತ್ತದ ಸುತ್ತಳತೆಯನ್ನು ಕಂಡುಹಿಡಿಯುವುದು ಹೇಗೆ
ವೃತ್ತದ ಸುತ್ತಳತೆಯನ್ನು ಕಂಡುಹಿಡಿಯುವುದು ಹೇಗೆ![]() ವೃತ್ತದ ಸುತ್ತಳತೆ ಎಷ್ಟು?
ವೃತ್ತದ ಸುತ್ತಳತೆ ಎಷ್ಟು?
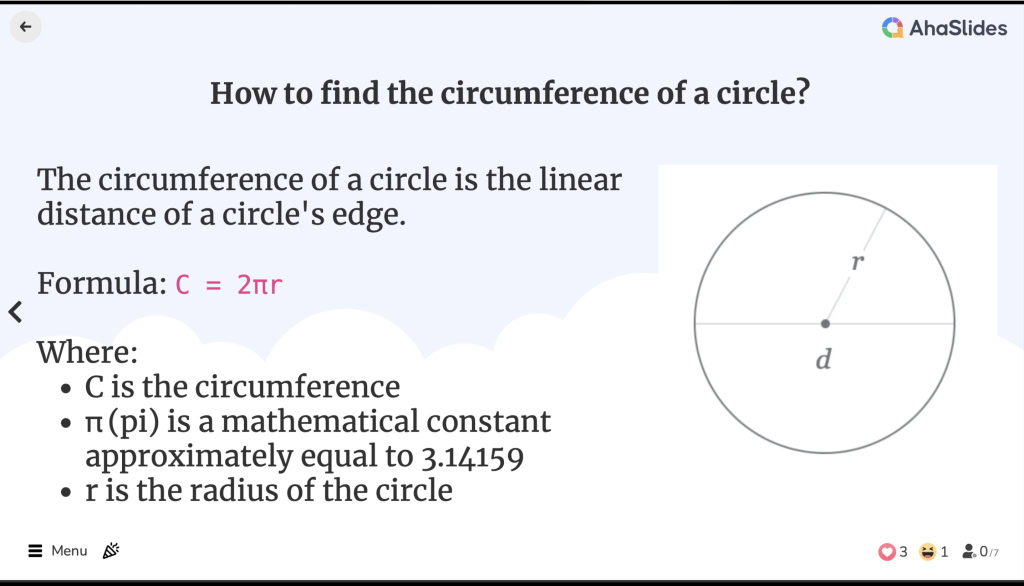
![]() ವೃತ್ತದ ಸುತ್ತಳತೆಯು ವೃತ್ತದ ಅಂಚಿನ ರೇಖೀಯ ಅಂತರವಾಗಿದೆ. ಇದು ಜ್ಯಾಮಿತೀಯ ಆಕಾರದ ಪರಿಧಿಗೆ ಸಮನಾಗಿರುತ್ತದೆ, ಆದಾಗ್ಯೂ ಪರಿಧಿ ಎಂಬ ಪದವನ್ನು ಬಹುಭುಜಾಕೃತಿಗಳಿಗೆ ಮಾತ್ರ ಬಳಸಲಾಗುತ್ತದೆ.
ವೃತ್ತದ ಸುತ್ತಳತೆಯು ವೃತ್ತದ ಅಂಚಿನ ರೇಖೀಯ ಅಂತರವಾಗಿದೆ. ಇದು ಜ್ಯಾಮಿತೀಯ ಆಕಾರದ ಪರಿಧಿಗೆ ಸಮನಾಗಿರುತ್ತದೆ, ಆದಾಗ್ಯೂ ಪರಿಧಿ ಎಂಬ ಪದವನ್ನು ಬಹುಭುಜಾಕೃತಿಗಳಿಗೆ ಮಾತ್ರ ಬಳಸಲಾಗುತ್ತದೆ.
![]() ವೃತ್ತದ ಸುತ್ತಳತೆಯನ್ನು ಕಂಡುಹಿಡಿಯುವುದು ಹೇಗೆ?
ವೃತ್ತದ ಸುತ್ತಳತೆಯನ್ನು ಕಂಡುಹಿಡಿಯುವುದು ಹೇಗೆ?
![]() ವೃತ್ತದ ಸೂತ್ರದ ಸುತ್ತಳತೆ:
ವೃತ್ತದ ಸೂತ್ರದ ಸುತ್ತಳತೆ:
C = 2πr
![]() ಅಲ್ಲಿ:
ಅಲ್ಲಿ:
 C ಎಂಬುದು ಸುತ್ತಳತೆ
C ಎಂಬುದು ಸುತ್ತಳತೆ π (ಪೈ) ಗಣಿತದ ಸ್ಥಿರಾಂಕವು ಸರಿಸುಮಾರು 3.14159 ಗೆ ಸಮಾನವಾಗಿರುತ್ತದೆ
π (ಪೈ) ಗಣಿತದ ಸ್ಥಿರಾಂಕವು ಸರಿಸುಮಾರು 3.14159 ಗೆ ಸಮಾನವಾಗಿರುತ್ತದೆ r ಎಂಬುದು ವೃತ್ತದ ತ್ರಿಜ್ಯವಾಗಿದೆ
r ಎಂಬುದು ವೃತ್ತದ ತ್ರಿಜ್ಯವಾಗಿದೆ
![]() ತ್ರಿಜ್ಯವು ವೃತ್ತದ ಮಧ್ಯಭಾಗದಿಂದ ಅಂಚಿನಲ್ಲಿರುವ ಯಾವುದೇ ಬಿಂದುವಿಗೆ ಇರುವ ಅಂತರವಾಗಿದೆ.
ತ್ರಿಜ್ಯವು ವೃತ್ತದ ಮಧ್ಯಭಾಗದಿಂದ ಅಂಚಿನಲ್ಲಿರುವ ಯಾವುದೇ ಬಿಂದುವಿಗೆ ಇರುವ ಅಂತರವಾಗಿದೆ.
![]() ವ್ಯಾಸವು ತ್ರಿಜ್ಯದ ಎರಡು ಪಟ್ಟು, ಆದ್ದರಿಂದ ಸುತ್ತಳತೆಯನ್ನು ಹೀಗೆ ವ್ಯಕ್ತಪಡಿಸಬಹುದು:
ವ್ಯಾಸವು ತ್ರಿಜ್ಯದ ಎರಡು ಪಟ್ಟು, ಆದ್ದರಿಂದ ಸುತ್ತಳತೆಯನ್ನು ಹೀಗೆ ವ್ಯಕ್ತಪಡಿಸಬಹುದು:
C = πd
![]() ಅಲ್ಲಿ:
ಅಲ್ಲಿ:
 d ವ್ಯಾಸವಾಗಿದೆ
d ವ್ಯಾಸವಾಗಿದೆ
![]() ಉದಾಹರಣೆಗೆ, ವೃತ್ತದ ತ್ರಿಜ್ಯವು 5 ಸೆಂ ಆಗಿದ್ದರೆ, ಆಗ ಸುತ್ತಳತೆ:
ಉದಾಹರಣೆಗೆ, ವೃತ್ತದ ತ್ರಿಜ್ಯವು 5 ಸೆಂ ಆಗಿದ್ದರೆ, ಆಗ ಸುತ್ತಳತೆ:
C = 2πr = 2π * 5 cm = 10π cm
![]() ≈ 31.4 ಸೆಂ (2 ದಶಮಾಂಶ ಸ್ಥಾನಗಳಿಗೆ ದುಂಡಾದ)
≈ 31.4 ಸೆಂ (2 ದಶಮಾಂಶ ಸ್ಥಾನಗಳಿಗೆ ದುಂಡಾದ)
 ಇವರಿಂದ ಇನ್ನಷ್ಟು ಸಲಹೆಗಳು AhaSlides
ಇವರಿಂದ ಇನ್ನಷ್ಟು ಸಲಹೆಗಳು AhaSlides
 ತರಗತಿಯಲ್ಲಿ ಮೋಜಿನ ವ್ಯಾಯಾಮಗಳಿಗಾಗಿ 70+ ಗಣಿತ ರಸಪ್ರಶ್ನೆ ಪ್ರಶ್ನೆಗಳು
ತರಗತಿಯಲ್ಲಿ ಮೋಜಿನ ವ್ಯಾಯಾಮಗಳಿಗಾಗಿ 70+ ಗಣಿತ ರಸಪ್ರಶ್ನೆ ಪ್ರಶ್ನೆಗಳು ಬೇಸರಗೊಂಡ K10 ವಿದ್ಯಾರ್ಥಿಗಳಿಗೆ 12 ಅತ್ಯುತ್ತಮ ತರಗತಿ ಗಣಿತ ಆಟಗಳು
ಬೇಸರಗೊಂಡ K10 ವಿದ್ಯಾರ್ಥಿಗಳಿಗೆ 12 ಅತ್ಯುತ್ತಮ ತರಗತಿ ಗಣಿತ ಆಟಗಳು ವಯಸ್ಕರಿಗೆ ಬ್ರೈನ್ ಟೀಸರ್ಗಳ ಕುರಿತು 60 ಅದ್ಭುತ ವಿಚಾರಗಳು | 2023 ನವೀಕರಣಗಳು
ವಯಸ್ಕರಿಗೆ ಬ್ರೈನ್ ಟೀಸರ್ಗಳ ಕುರಿತು 60 ಅದ್ಭುತ ವಿಚಾರಗಳು | 2023 ನವೀಕರಣಗಳು
![]() AhaSlides ಅಲ್ಟಿಮೇಟ್ ಕ್ವಿಜ್ ಮೇಕರ್ ಆಗಿದೆ
AhaSlides ಅಲ್ಟಿಮೇಟ್ ಕ್ವಿಜ್ ಮೇಕರ್ ಆಗಿದೆ
![]() ಬೇಸರವನ್ನು ಹೋಗಲಾಡಿಸಲು ನಮ್ಮ ವ್ಯಾಪಕವಾದ ಟೆಂಪ್ಲೇಟ್ ಲೈಬ್ರರಿಯೊಂದಿಗೆ ಕ್ಷಣಾರ್ಧದಲ್ಲಿ ಸಂವಾದಾತ್ಮಕ ಆಟಗಳನ್ನು ಮಾಡಿ
ಬೇಸರವನ್ನು ಹೋಗಲಾಡಿಸಲು ನಮ್ಮ ವ್ಯಾಪಕವಾದ ಟೆಂಪ್ಲೇಟ್ ಲೈಬ್ರರಿಯೊಂದಿಗೆ ಕ್ಷಣಾರ್ಧದಲ್ಲಿ ಸಂವಾದಾತ್ಮಕ ಆಟಗಳನ್ನು ಮಾಡಿ

 ಬೇಸರಗೊಂಡಾಗ ಆಡಲು ಆನ್ಲೈನ್ ಆಟಗಳು
ಬೇಸರಗೊಂಡಾಗ ಆಡಲು ಆನ್ಲೈನ್ ಆಟಗಳು ವೃತ್ತ ರಸಪ್ರಶ್ನೆಯ ಸುತ್ತಳತೆ
ವೃತ್ತ ರಸಪ್ರಶ್ನೆಯ ಸುತ್ತಳತೆ
![]() ಪ್ರಶ್ನೆ 1: ವೃತ್ತಾಕಾರದ ಈಜುಕೊಳದ ಸುತ್ತಳತೆ 50 ಮೀಟರ್ ಆಗಿದ್ದರೆ, ಅದರ ತ್ರಿಜ್ಯ ಎಷ್ಟು?
ಪ್ರಶ್ನೆ 1: ವೃತ್ತಾಕಾರದ ಈಜುಕೊಳದ ಸುತ್ತಳತೆ 50 ಮೀಟರ್ ಆಗಿದ್ದರೆ, ಅದರ ತ್ರಿಜ್ಯ ಎಷ್ಟು?
![]() A. 7.95 ಮೀಟರ್
A. 7.95 ಮೀಟರ್
![]() ಬಿ. 8.00 ಮೀಟರ್
ಬಿ. 8.00 ಮೀಟರ್
![]() C. 15.91 ಮೀಟರ್
C. 15.91 ಮೀಟರ್
![]() D. 25 ಮೀಟರ್
D. 25 ಮೀಟರ್
✅ ![]() ಸರಿಯಾದ ಉತ್ತರ:
ಸರಿಯಾದ ಉತ್ತರ:
![]() A. 7.95 ಮೀಟರ್
A. 7.95 ಮೀಟರ್
![]() ವಿವರಣೆ:
ವಿವರಣೆ:
![]() C = 2πr ಸೂತ್ರವನ್ನು ಮರುಹೊಂದಿಸಿ ಮತ್ತು r: r = C / (2π) ಗಾಗಿ ಪರಿಹರಿಸುವ ಮೂಲಕ ತ್ರಿಜ್ಯವನ್ನು ಕಂಡುಹಿಡಿಯಬಹುದು. ನೀಡಲಾದ 50 ಮೀಟರ್ಗಳ ಸುತ್ತಳತೆಯನ್ನು ಪ್ಲಗ್ ಮಾಡುವುದು ಮತ್ತು π ರಿಂದ 3.14 ರ ಅಂದಾಜು ಮಾಡುವುದರಿಂದ, ನಾವು ತ್ರಿಜ್ಯವು ಸರಿಸುಮಾರು 7.95 ಮೀಟರ್ಗಳು ಎಂದು ಕಂಡುಕೊಳ್ಳುತ್ತೇವೆ.
C = 2πr ಸೂತ್ರವನ್ನು ಮರುಹೊಂದಿಸಿ ಮತ್ತು r: r = C / (2π) ಗಾಗಿ ಪರಿಹರಿಸುವ ಮೂಲಕ ತ್ರಿಜ್ಯವನ್ನು ಕಂಡುಹಿಡಿಯಬಹುದು. ನೀಡಲಾದ 50 ಮೀಟರ್ಗಳ ಸುತ್ತಳತೆಯನ್ನು ಪ್ಲಗ್ ಮಾಡುವುದು ಮತ್ತು π ರಿಂದ 3.14 ರ ಅಂದಾಜು ಮಾಡುವುದರಿಂದ, ನಾವು ತ್ರಿಜ್ಯವು ಸರಿಸುಮಾರು 7.95 ಮೀಟರ್ಗಳು ಎಂದು ಕಂಡುಕೊಳ್ಳುತ್ತೇವೆ.
![]() ಪ್ರಶ್ನೆ 2: ವೃತ್ತದ ವ್ಯಾಸವು 14 ಇಂಚುಗಳು. ಅದರ ತ್ರಿಜ್ಯ ಏನು?
ಪ್ರಶ್ನೆ 2: ವೃತ್ತದ ವ್ಯಾಸವು 14 ಇಂಚುಗಳು. ಅದರ ತ್ರಿಜ್ಯ ಏನು?
![]() A. 28 ಇಂಚುಗಳು
A. 28 ಇಂಚುಗಳು
![]() ಬಿ.14 ಇಂಚುಗಳು
ಬಿ.14 ಇಂಚುಗಳು
![]() C. 21 ಇಂಚುಗಳು
C. 21 ಇಂಚುಗಳು
![]() D. 7 ಇಂಚುಗಳು
D. 7 ಇಂಚುಗಳು
✅ ![]() ಸರಿಯಾದ ಉತ್ತರ:
ಸರಿಯಾದ ಉತ್ತರ:
![]() D. 7 ಇಂಚುಗಳು
D. 7 ಇಂಚುಗಳು
![]() ವಿವರಣೆ:
ವಿವರಣೆ:
![]() ವ್ಯಾಸವು ತ್ರಿಜ್ಯದ ಎರಡು ಪಟ್ಟು ಉದ್ದವಾಗಿರುವುದರಿಂದ (d = 2r), ವ್ಯಾಸವನ್ನು 2 ರಿಂದ ಭಾಗಿಸುವ ಮೂಲಕ ನೀವು ತ್ರಿಜ್ಯವನ್ನು ಕಂಡುಹಿಡಿಯಬಹುದು (r = d / 2). ಈ ಸಂದರ್ಭದಲ್ಲಿ, 14 ಇಂಚುಗಳ ನೀಡಿದ ವ್ಯಾಸವನ್ನು 2 ರಿಂದ ಭಾಗಿಸಿದರೆ a 7 ಇಂಚುಗಳ ತ್ರಿಜ್ಯ.
ವ್ಯಾಸವು ತ್ರಿಜ್ಯದ ಎರಡು ಪಟ್ಟು ಉದ್ದವಾಗಿರುವುದರಿಂದ (d = 2r), ವ್ಯಾಸವನ್ನು 2 ರಿಂದ ಭಾಗಿಸುವ ಮೂಲಕ ನೀವು ತ್ರಿಜ್ಯವನ್ನು ಕಂಡುಹಿಡಿಯಬಹುದು (r = d / 2). ಈ ಸಂದರ್ಭದಲ್ಲಿ, 14 ಇಂಚುಗಳ ನೀಡಿದ ವ್ಯಾಸವನ್ನು 2 ರಿಂದ ಭಾಗಿಸಿದರೆ a 7 ಇಂಚುಗಳ ತ್ರಿಜ್ಯ.

 ವೃತ್ತದ ಸುತ್ತಳತೆಯನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ
ವೃತ್ತದ ಸುತ್ತಳತೆಯನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ![]() ಪ್ರಶ್ನೆ 3: ವೃತ್ತದ ವ್ಯಾಸ ಮತ್ತು ಸುತ್ತಳತೆಯ ನಡುವಿನ ಸಂಬಂಧದ ಬಗ್ಗೆ ಈ ಕೆಳಗಿನ ಯಾವ ಹೇಳಿಕೆಗಳು ನಿಜವಾಗಿದೆ?
ಪ್ರಶ್ನೆ 3: ವೃತ್ತದ ವ್ಯಾಸ ಮತ್ತು ಸುತ್ತಳತೆಯ ನಡುವಿನ ಸಂಬಂಧದ ಬಗ್ಗೆ ಈ ಕೆಳಗಿನ ಯಾವ ಹೇಳಿಕೆಗಳು ನಿಜವಾಗಿದೆ?
![]() A. ವ್ಯಾಸವು ಅರ್ಧದಷ್ಟು ಸುತ್ತಳತೆಯಾಗಿದೆ.
A. ವ್ಯಾಸವು ಅರ್ಧದಷ್ಟು ಸುತ್ತಳತೆಯಾಗಿದೆ.
![]() B. ವ್ಯಾಸವು ಸುತ್ತಳತೆಯಂತೆಯೇ ಇರುತ್ತದೆ.
B. ವ್ಯಾಸವು ಸುತ್ತಳತೆಯಂತೆಯೇ ಇರುತ್ತದೆ.
![]() C. ವ್ಯಾಸವು ಸುತ್ತಳತೆಯ ಎರಡು ಪಟ್ಟು.
C. ವ್ಯಾಸವು ಸುತ್ತಳತೆಯ ಎರಡು ಪಟ್ಟು.
![]() D. ವ್ಯಾಸವು ಸುತ್ತಳತೆಯ π ಪಟ್ಟು.
D. ವ್ಯಾಸವು ಸುತ್ತಳತೆಯ π ಪಟ್ಟು.
✅ ![]() ಸರಿಯಾದ ಉತ್ತರ:
ಸರಿಯಾದ ಉತ್ತರ:
![]() A. ವ್ಯಾಸವು ಅರ್ಧದಷ್ಟು ಸುತ್ತಳತೆಯಾಗಿದೆ.
A. ವ್ಯಾಸವು ಅರ್ಧದಷ್ಟು ಸುತ್ತಳತೆಯಾಗಿದೆ.
![]() ವಿವರಣೆ:
ವಿವರಣೆ:
![]() ವ್ಯಾಸವು ತ್ರಿಜ್ಯದ 2 ಪಟ್ಟು ಸಮಾನವಾಗಿರುತ್ತದೆ, ಆದರೆ ಸುತ್ತಳತೆಯು ತ್ರಿಜ್ಯದ 2π ಪಟ್ಟು ಸಮಾನವಾಗಿರುತ್ತದೆ. ಆದ್ದರಿಂದ, ವ್ಯಾಸವು ಅರ್ಧದಷ್ಟು ಸುತ್ತಳತೆಯಾಗಿದೆ.
ವ್ಯಾಸವು ತ್ರಿಜ್ಯದ 2 ಪಟ್ಟು ಸಮಾನವಾಗಿರುತ್ತದೆ, ಆದರೆ ಸುತ್ತಳತೆಯು ತ್ರಿಜ್ಯದ 2π ಪಟ್ಟು ಸಮಾನವಾಗಿರುತ್ತದೆ. ಆದ್ದರಿಂದ, ವ್ಯಾಸವು ಅರ್ಧದಷ್ಟು ಸುತ್ತಳತೆಯಾಗಿದೆ.
![]() ಪ್ರಶ್ನೆ 4: ನಾವು ಕುಳಿತುಕೊಳ್ಳಬೇಕಾದ ಟೇಬಲ್ 6.28 ಗಜಗಳ ಸುತ್ತಳತೆಯನ್ನು ಹೊಂದಿದೆ. ನಾವು ಮೇಜಿನ ವ್ಯಾಸವನ್ನು ಕಂಡುಹಿಡಿಯಬೇಕು.
ಪ್ರಶ್ನೆ 4: ನಾವು ಕುಳಿತುಕೊಳ್ಳಬೇಕಾದ ಟೇಬಲ್ 6.28 ಗಜಗಳ ಸುತ್ತಳತೆಯನ್ನು ಹೊಂದಿದೆ. ನಾವು ಮೇಜಿನ ವ್ಯಾಸವನ್ನು ಕಂಡುಹಿಡಿಯಬೇಕು.
![]() A. 1 ಗಜ
A. 1 ಗಜ
![]() B. 2 ಗಜಗಳು
B. 2 ಗಜಗಳು
![]() C. 3 ಗಜಗಳು
C. 3 ಗಜಗಳು
![]() D. 4 ಗಜಗಳು
D. 4 ಗಜಗಳು
✅ ![]() ಸರಿಯಾದ ಉತ್ತರ:
ಸರಿಯಾದ ಉತ್ತರ:
![]() B. 2 ಗಜಗಳು
B. 2 ಗಜಗಳು
![]() ವಿವರಣೆ:
ವಿವರಣೆ:
![]() ವೃತ್ತದ ಸುತ್ತಳತೆಯನ್ನು ಪೈ (π) ನಿಂದ ವ್ಯಾಸವನ್ನು ಗುಣಿಸುವ ಮೂಲಕ ಲೆಕ್ಕಹಾಕಲಾಗುತ್ತದೆ. ಈ ಸಂದರ್ಭದಲ್ಲಿ, ಸುತ್ತಳತೆಯನ್ನು 6.28 ಗಜ ಎಂದು ನೀಡಲಾಗಿದೆ. ವ್ಯಾಸವನ್ನು ಕಂಡುಹಿಡಿಯಲು, ನಾವು ಸುತ್ತಳತೆಯನ್ನು ಪೈ ಮೂಲಕ ಭಾಗಿಸಬೇಕಾಗಿದೆ. 6.28 ಗಜಗಳನ್ನು ಪೈನಿಂದ ಭಾಗಿಸಿದಾಗ ನಮಗೆ ಸರಿಸುಮಾರು 2 ಗಜಗಳು ಸಿಗುತ್ತವೆ. ಆದ್ದರಿಂದ, ಮೇಜಿನ ವ್ಯಾಸವು 2 ಗಜಗಳು.
ವೃತ್ತದ ಸುತ್ತಳತೆಯನ್ನು ಪೈ (π) ನಿಂದ ವ್ಯಾಸವನ್ನು ಗುಣಿಸುವ ಮೂಲಕ ಲೆಕ್ಕಹಾಕಲಾಗುತ್ತದೆ. ಈ ಸಂದರ್ಭದಲ್ಲಿ, ಸುತ್ತಳತೆಯನ್ನು 6.28 ಗಜ ಎಂದು ನೀಡಲಾಗಿದೆ. ವ್ಯಾಸವನ್ನು ಕಂಡುಹಿಡಿಯಲು, ನಾವು ಸುತ್ತಳತೆಯನ್ನು ಪೈ ಮೂಲಕ ಭಾಗಿಸಬೇಕಾಗಿದೆ. 6.28 ಗಜಗಳನ್ನು ಪೈನಿಂದ ಭಾಗಿಸಿದಾಗ ನಮಗೆ ಸರಿಸುಮಾರು 2 ಗಜಗಳು ಸಿಗುತ್ತವೆ. ಆದ್ದರಿಂದ, ಮೇಜಿನ ವ್ಯಾಸವು 2 ಗಜಗಳು.
![]() ಪ್ರಶ್ನೆ 5: ವೃತ್ತಾಕಾರದ ಉದ್ಯಾನವು 36 ಮೀಟರ್ ಸುತ್ತಳತೆಯನ್ನು ಹೊಂದಿದೆ. ಉದ್ಯಾನದ ಅಂದಾಜು ತ್ರಿಜ್ಯ ಎಷ್ಟು?
ಪ್ರಶ್ನೆ 5: ವೃತ್ತಾಕಾರದ ಉದ್ಯಾನವು 36 ಮೀಟರ್ ಸುತ್ತಳತೆಯನ್ನು ಹೊಂದಿದೆ. ಉದ್ಯಾನದ ಅಂದಾಜು ತ್ರಿಜ್ಯ ಎಷ್ಟು?
![]() A. 3.14 ಮೀಟರ್
A. 3.14 ಮೀಟರ್
![]() ಬಿ. 6 ಮೀಟರ್
ಬಿ. 6 ಮೀಟರ್
![]() C. 9 ಮೀಟರ್
C. 9 ಮೀಟರ್
![]() D. 18 ಮೀಟರ್
D. 18 ಮೀಟರ್
✅ ![]() ಸರಿಯಾದ ಉತ್ತರ:
ಸರಿಯಾದ ಉತ್ತರ:
![]() C. 9 ಮೀಟರ್
C. 9 ಮೀಟರ್
![]() ವಿವರಣೆ:
ವಿವರಣೆ:
![]() ತ್ರಿಜ್ಯವನ್ನು ಕಂಡುಹಿಡಿಯಲು, ಸುತ್ತಳತೆಗೆ ಸೂತ್ರವನ್ನು ಬಳಸಿ: C = 2πr. ತ್ರಿಜ್ಯವನ್ನು ಪರಿಹರಿಸಲು ಸೂತ್ರವನ್ನು ಮರುಹೊಂದಿಸಿ: r = C / (2π). ನೀಡಲಾದ 36 ಮೀಟರ್ಗಳ ಸುತ್ತಳತೆಯನ್ನು ಪ್ಲಗ್ ಮಾಡುವುದು ಮತ್ತು π ನ ಅಂದಾಜು ಮೌಲ್ಯವನ್ನು 3.14 ನಂತೆ ಬಳಸಿದರೆ, ನೀವು r = 36 / (2 * 3.14) ≈ 9 ಮೀಟರ್ಗಳನ್ನು ಪಡೆಯುತ್ತೀರಿ.
ತ್ರಿಜ್ಯವನ್ನು ಕಂಡುಹಿಡಿಯಲು, ಸುತ್ತಳತೆಗೆ ಸೂತ್ರವನ್ನು ಬಳಸಿ: C = 2πr. ತ್ರಿಜ್ಯವನ್ನು ಪರಿಹರಿಸಲು ಸೂತ್ರವನ್ನು ಮರುಹೊಂದಿಸಿ: r = C / (2π). ನೀಡಲಾದ 36 ಮೀಟರ್ಗಳ ಸುತ್ತಳತೆಯನ್ನು ಪ್ಲಗ್ ಮಾಡುವುದು ಮತ್ತು π ನ ಅಂದಾಜು ಮೌಲ್ಯವನ್ನು 3.14 ನಂತೆ ಬಳಸಿದರೆ, ನೀವು r = 36 / (2 * 3.14) ≈ 9 ಮೀಟರ್ಗಳನ್ನು ಪಡೆಯುತ್ತೀರಿ.
![]() ಪ್ರಶ್ನೆ 6: ವೃತ್ತಾಕಾರದ ಈಜುಕೊಳವು 8 ಮೀಟರ್ ತ್ರಿಜ್ಯವನ್ನು ಹೊಂದಿದೆ. ಒಂದು ಲ್ಯಾಪ್ ಅನ್ನು ಪೂರ್ಣಗೊಳಿಸಿದಾಗ ಈಜುಗಾರ ಕೊಳದ ಸುತ್ತಲೂ ಪ್ರಯಾಣಿಸುವ ಅಂದಾಜು ದೂರ ಎಷ್ಟು?
ಪ್ರಶ್ನೆ 6: ವೃತ್ತಾಕಾರದ ಈಜುಕೊಳವು 8 ಮೀಟರ್ ತ್ರಿಜ್ಯವನ್ನು ಹೊಂದಿದೆ. ಒಂದು ಲ್ಯಾಪ್ ಅನ್ನು ಪೂರ್ಣಗೊಳಿಸಿದಾಗ ಈಜುಗಾರ ಕೊಳದ ಸುತ್ತಲೂ ಪ್ರಯಾಣಿಸುವ ಅಂದಾಜು ದೂರ ಎಷ್ಟು?
![]() A. 16 ಮೀಟರ್
A. 16 ಮೀಟರ್
![]() ಬಿ. 25 ಮೀಟರ್
ಬಿ. 25 ಮೀಟರ್
![]() C. 50 ಮೀಟರ್
C. 50 ಮೀಟರ್
![]() D. 100 ಮೀಟರ್
D. 100 ಮೀಟರ್
✅ ![]() ಸರಿಯಾದ ಉತ್ತರ:
ಸರಿಯಾದ ಉತ್ತರ:
![]() C. 50 ಮೀಟರ್
C. 50 ಮೀಟರ್
![]() ವಿವರಣೆ:
ವಿವರಣೆ:
![]() ಈಜುಗಾರನು ಒಂದು ಸುತ್ತಿಗೆ ಕೊಳದ ಸುತ್ತಲೂ ಪ್ರಯಾಣಿಸುವ ದೂರವನ್ನು ಕಂಡುಹಿಡಿಯಲು, ನೀವು ಸುತ್ತಳತೆ ಸೂತ್ರವನ್ನು (C = 2πr) ಬಳಸಿ. ಈ ಸಂದರ್ಭದಲ್ಲಿ, ಇದು 2 * 3.14 * 8 ಮೀಟರ್ ≈ 50.24 ಮೀಟರ್, ಇದು ಸರಿಸುಮಾರು 50 ಮೀಟರ್.
ಈಜುಗಾರನು ಒಂದು ಸುತ್ತಿಗೆ ಕೊಳದ ಸುತ್ತಲೂ ಪ್ರಯಾಣಿಸುವ ದೂರವನ್ನು ಕಂಡುಹಿಡಿಯಲು, ನೀವು ಸುತ್ತಳತೆ ಸೂತ್ರವನ್ನು (C = 2πr) ಬಳಸಿ. ಈ ಸಂದರ್ಭದಲ್ಲಿ, ಇದು 2 * 3.14 * 8 ಮೀಟರ್ ≈ 50.24 ಮೀಟರ್, ಇದು ಸರಿಸುಮಾರು 50 ಮೀಟರ್.
![]() ಪ್ರಶ್ನೆ 7: ಕ್ಲಾಸ್ನಲ್ಲಿ ಹುಲಾ ಹೂಪ್ ಅನ್ನು ಅಳೆಯುವಾಗ, ಗುಂಪು C ಇದು 7 ಇಂಚುಗಳಷ್ಟು ತ್ರಿಜ್ಯವನ್ನು ಹೊಂದಿದೆ ಎಂದು ಕಂಡುಹಿಡಿದಿದೆ. ಹುಲಾ ಹೂಪ್ನ ಸುತ್ತಳತೆ ಏನು?
ಪ್ರಶ್ನೆ 7: ಕ್ಲಾಸ್ನಲ್ಲಿ ಹುಲಾ ಹೂಪ್ ಅನ್ನು ಅಳೆಯುವಾಗ, ಗುಂಪು C ಇದು 7 ಇಂಚುಗಳಷ್ಟು ತ್ರಿಜ್ಯವನ್ನು ಹೊಂದಿದೆ ಎಂದು ಕಂಡುಹಿಡಿದಿದೆ. ಹುಲಾ ಹೂಪ್ನ ಸುತ್ತಳತೆ ಏನು?
![]() A. 39.6 ಇಂಚುಗಳು
A. 39.6 ಇಂಚುಗಳು
![]() B. 37.6 ಇಂಚುಗಳು
B. 37.6 ಇಂಚುಗಳು
![]() C. 47.6 ಇಂಚುಗಳು
C. 47.6 ಇಂಚುಗಳು
![]() D. 49.6 ಇಂಚುಗಳು
D. 49.6 ಇಂಚುಗಳು
✅ ![]() ಸರಿಯಾದ ಉತ್ತರ:
ಸರಿಯಾದ ಉತ್ತರ:
![]() C. 47.6 ಇಂಚುಗಳು
C. 47.6 ಇಂಚುಗಳು
![]() ವಿವರಣೆ:
ವಿವರಣೆ:
![]() C = 2πr ಸೂತ್ರವನ್ನು ಬಳಸಿಕೊಂಡು ವೃತ್ತದ ಸುತ್ತಳತೆಯನ್ನು ಕಂಡುಹಿಡಿಯಬಹುದು, ಇಲ್ಲಿ r ವೃತ್ತದ ತ್ರಿಜ್ಯವಾಗಿದೆ. ಈ ಸಂದರ್ಭದಲ್ಲಿ, ಹುಲಾ ಹೂಪ್ನ ತ್ರಿಜ್ಯವನ್ನು 7 ಇಂಚುಗಳಾಗಿ ನೀಡಲಾಗುತ್ತದೆ. ಈ ಮೌಲ್ಯವನ್ನು ಸೂತ್ರಕ್ಕೆ ಪ್ಲಗ್ ಮಾಡುವುದರಿಂದ, ನಾವು C = 2π (7) = 14π ಇಂಚುಗಳನ್ನು ಪಡೆಯುತ್ತೇವೆ. ಅಂದಾಜು π ರಿಂದ 3.14, ನಾವು ಸುತ್ತಳತೆಯನ್ನು 14(3.14) = 43.96 ಇಂಚುಗಳಾಗಿ ಲೆಕ್ಕ ಹಾಕಬಹುದು. ಹತ್ತಿರದ ಹತ್ತನೆಯದಕ್ಕೆ ದುಂಡಾದ, ಸುತ್ತಳತೆ 47.6 ಇಂಚುಗಳು, ಇದು ನೀಡಿದ ಉತ್ತರಕ್ಕೆ ಹೊಂದಿಕೆಯಾಗುತ್ತದೆ.
C = 2πr ಸೂತ್ರವನ್ನು ಬಳಸಿಕೊಂಡು ವೃತ್ತದ ಸುತ್ತಳತೆಯನ್ನು ಕಂಡುಹಿಡಿಯಬಹುದು, ಇಲ್ಲಿ r ವೃತ್ತದ ತ್ರಿಜ್ಯವಾಗಿದೆ. ಈ ಸಂದರ್ಭದಲ್ಲಿ, ಹುಲಾ ಹೂಪ್ನ ತ್ರಿಜ್ಯವನ್ನು 7 ಇಂಚುಗಳಾಗಿ ನೀಡಲಾಗುತ್ತದೆ. ಈ ಮೌಲ್ಯವನ್ನು ಸೂತ್ರಕ್ಕೆ ಪ್ಲಗ್ ಮಾಡುವುದರಿಂದ, ನಾವು C = 2π (7) = 14π ಇಂಚುಗಳನ್ನು ಪಡೆಯುತ್ತೇವೆ. ಅಂದಾಜು π ರಿಂದ 3.14, ನಾವು ಸುತ್ತಳತೆಯನ್ನು 14(3.14) = 43.96 ಇಂಚುಗಳಾಗಿ ಲೆಕ್ಕ ಹಾಕಬಹುದು. ಹತ್ತಿರದ ಹತ್ತನೆಯದಕ್ಕೆ ದುಂಡಾದ, ಸುತ್ತಳತೆ 47.6 ಇಂಚುಗಳು, ಇದು ನೀಡಿದ ಉತ್ತರಕ್ಕೆ ಹೊಂದಿಕೆಯಾಗುತ್ತದೆ.
![]() ಪ್ರಶ್ನೆ 8: ಅರ್ಧವೃತ್ತವು 10 ಮೀಟರ್ ತ್ರಿಜ್ಯವನ್ನು ಹೊಂದಿದೆ. ಅದರ ಪರಿಧಿ ಏನು?
ಪ್ರಶ್ನೆ 8: ಅರ್ಧವೃತ್ತವು 10 ಮೀಟರ್ ತ್ರಿಜ್ಯವನ್ನು ಹೊಂದಿದೆ. ಅದರ ಪರಿಧಿ ಏನು?
![]() A. 20 ಮೀಟರ್
A. 20 ಮೀಟರ್
![]() ಬಿ. 15 ಮೀಟರ್
ಬಿ. 15 ಮೀಟರ್
![]() C. 31.42 ಮೀಟರ್
C. 31.42 ಮೀಟರ್
![]() D. 62.84 ಮೀಟರ್
D. 62.84 ಮೀಟರ್
✅ ![]() ಸರಿಯಾದ ಉತ್ತರ:
ಸರಿಯಾದ ಉತ್ತರ:
![]() C. 31.42 ಮೀಟರ್
C. 31.42 ಮೀಟರ್
![]() ವಿವರಣೆ:
ವಿವರಣೆ:![]() ಅರ್ಧವೃತ್ತದ ಪರಿಧಿಯನ್ನು ಕಂಡುಹಿಡಿಯಲು, 10 ಮೀಟರ್ ತ್ರಿಜ್ಯದೊಂದಿಗೆ ಪೂರ್ಣ ವೃತ್ತದ ಅರ್ಧದಷ್ಟು ಸುತ್ತಳತೆಯನ್ನು ಲೆಕ್ಕಹಾಕಿ.
ಅರ್ಧವೃತ್ತದ ಪರಿಧಿಯನ್ನು ಕಂಡುಹಿಡಿಯಲು, 10 ಮೀಟರ್ ತ್ರಿಜ್ಯದೊಂದಿಗೆ ಪೂರ್ಣ ವೃತ್ತದ ಅರ್ಧದಷ್ಟು ಸುತ್ತಳತೆಯನ್ನು ಲೆಕ್ಕಹಾಕಿ.

 ವೃತ್ತದ ಉದಾಹರಣೆಯ ಸುತ್ತಳತೆ
ವೃತ್ತದ ಉದಾಹರಣೆಯ ಸುತ್ತಳತೆ![]() ಪ್ರಶ್ನೆ 9: ಬ್ಯಾಸ್ಕೆಟ್ಬಾಲ್ ತಂಡವು 5.6 ಇಂಚುಗಳಷ್ಟು ತ್ರಿಜ್ಯವಿರುವ ಚೆಂಡಿನೊಂದಿಗೆ ಆಡುತ್ತದೆ. ಪ್ರತಿ ಬ್ಯಾಸ್ಕೆಟ್ಬಾಲ್ನ ಸುತ್ತಳತೆ ಎಷ್ಟು?
ಪ್ರಶ್ನೆ 9: ಬ್ಯಾಸ್ಕೆಟ್ಬಾಲ್ ತಂಡವು 5.6 ಇಂಚುಗಳಷ್ಟು ತ್ರಿಜ್ಯವಿರುವ ಚೆಂಡಿನೊಂದಿಗೆ ಆಡುತ್ತದೆ. ಪ್ರತಿ ಬ್ಯಾಸ್ಕೆಟ್ಬಾಲ್ನ ಸುತ್ತಳತೆ ಎಷ್ಟು?
![]() A. 11.2 ಇಂಚುಗಳು
A. 11.2 ಇಂಚುಗಳು
![]() B. 17.6 ಇಂಚುಗಳು
B. 17.6 ಇಂಚುಗಳು
![]() C. 22.4 ಇಂಚುಗಳು
C. 22.4 ಇಂಚುಗಳು
![]() D. 35.2 ಇಂಚುಗಳು
D. 35.2 ಇಂಚುಗಳು
✅ ![]() ಸರಿಯಾದ ಉತ್ತರ:
ಸರಿಯಾದ ಉತ್ತರ:
![]() C. 22.4 ಇಂಚುಗಳು
C. 22.4 ಇಂಚುಗಳು
![]() ವಿವರಣೆ:
ವಿವರಣೆ:
![]() ವೃತ್ತದ ಸುತ್ತಳತೆಗೆ ನೀವು ಸೂತ್ರವನ್ನು ಬಳಸಬಹುದು, ಅದು C = 2πr ಆಗಿದೆ. ನೀಡಿರುವ ತ್ರಿಜ್ಯವು 5.6 ಇಂಚುಗಳು. ಈ ಮೌಲ್ಯವನ್ನು ಸೂತ್ರಕ್ಕೆ ಪ್ಲಗ್ ಮಾಡಿ, ನಾವು C = 2π * 5.6 ಇಂಚುಗಳನ್ನು ಹೊಂದಿದ್ದೇವೆ. C ≈ 2 * 3.14 * 5.6 ಇಂಚುಗಳು. C ≈ 11.2 * 5.6 ಇಂಚುಗಳು. C ≈ 22.4 ಇಂಚುಗಳು. ಆದ್ದರಿಂದ, ಪ್ರತಿ ಬ್ಯಾಸ್ಕೆಟ್ಬಾಲ್ನ ಸುತ್ತಳತೆ ಸರಿಸುಮಾರು 22.4 ಇಂಚುಗಳು. ಇದು ಬ್ಯಾಸ್ಕೆಟ್ಬಾಲ್ ಸುತ್ತಲಿನ ಅಂತರವನ್ನು ಪ್ರತಿನಿಧಿಸುತ್ತದೆ.
ವೃತ್ತದ ಸುತ್ತಳತೆಗೆ ನೀವು ಸೂತ್ರವನ್ನು ಬಳಸಬಹುದು, ಅದು C = 2πr ಆಗಿದೆ. ನೀಡಿರುವ ತ್ರಿಜ್ಯವು 5.6 ಇಂಚುಗಳು. ಈ ಮೌಲ್ಯವನ್ನು ಸೂತ್ರಕ್ಕೆ ಪ್ಲಗ್ ಮಾಡಿ, ನಾವು C = 2π * 5.6 ಇಂಚುಗಳನ್ನು ಹೊಂದಿದ್ದೇವೆ. C ≈ 2 * 3.14 * 5.6 ಇಂಚುಗಳು. C ≈ 11.2 * 5.6 ಇಂಚುಗಳು. C ≈ 22.4 ಇಂಚುಗಳು. ಆದ್ದರಿಂದ, ಪ್ರತಿ ಬ್ಯಾಸ್ಕೆಟ್ಬಾಲ್ನ ಸುತ್ತಳತೆ ಸರಿಸುಮಾರು 22.4 ಇಂಚುಗಳು. ಇದು ಬ್ಯಾಸ್ಕೆಟ್ಬಾಲ್ ಸುತ್ತಲಿನ ಅಂತರವನ್ನು ಪ್ರತಿನಿಧಿಸುತ್ತದೆ.
![]() ಪ್ರಶ್ನೆ 10: ಸಾರಾ ಮತ್ತು ಅವಳ ಇಬ್ಬರು ಸ್ನೇಹಿತರು ತಮ್ಮ ಸಭೆಗಾಗಿ ವೃತ್ತಾಕಾರದ ಪಿಕ್ನಿಕ್ ಟೇಬಲ್ ಅನ್ನು ನಿರ್ಮಿಸುತ್ತಿದ್ದರು. ಅವರೆಲ್ಲರೂ ಆರಾಮವಾಗಿ ಮೇಜಿನ ಸುತ್ತಲೂ ಕುಳಿತುಕೊಳ್ಳಲು, ಅವರಿಗೆ 18 ಅಡಿ ಸುತ್ತಳತೆ ಬೇಕು ಎಂದು ಅವರಿಗೆ ತಿಳಿದಿತ್ತು. ಸರಿಯಾದ ಸುತ್ತಳತೆಯನ್ನು ಸಾಧಿಸಲು ಪಿಕ್ನಿಕ್ ಟೇಬಲ್ ಯಾವ ವ್ಯಾಸವನ್ನು ಹೊಂದಿರಬೇಕು?
ಪ್ರಶ್ನೆ 10: ಸಾರಾ ಮತ್ತು ಅವಳ ಇಬ್ಬರು ಸ್ನೇಹಿತರು ತಮ್ಮ ಸಭೆಗಾಗಿ ವೃತ್ತಾಕಾರದ ಪಿಕ್ನಿಕ್ ಟೇಬಲ್ ಅನ್ನು ನಿರ್ಮಿಸುತ್ತಿದ್ದರು. ಅವರೆಲ್ಲರೂ ಆರಾಮವಾಗಿ ಮೇಜಿನ ಸುತ್ತಲೂ ಕುಳಿತುಕೊಳ್ಳಲು, ಅವರಿಗೆ 18 ಅಡಿ ಸುತ್ತಳತೆ ಬೇಕು ಎಂದು ಅವರಿಗೆ ತಿಳಿದಿತ್ತು. ಸರಿಯಾದ ಸುತ್ತಳತೆಯನ್ನು ಸಾಧಿಸಲು ಪಿಕ್ನಿಕ್ ಟೇಬಲ್ ಯಾವ ವ್ಯಾಸವನ್ನು ಹೊಂದಿರಬೇಕು?
![]() A. 3 ಅಡಿ
A. 3 ಅಡಿ
![]() ಬಿ. 6 ಅಡಿ
ಬಿ. 6 ಅಡಿ
![]() C. 9 ಅಡಿ
C. 9 ಅಡಿ
![]() D. 12 ಅಡಿ
D. 12 ಅಡಿ
✅ ![]() ಸರಿಯಾದ ಉತ್ತರ:
ಸರಿಯಾದ ಉತ್ತರ:
![]() ಬಿ. 6 ಅಡಿ
ಬಿ. 6 ಅಡಿ
![]() ವಿವರಣೆ:
ವಿವರಣೆ:
![]() ತ್ರಿಜ್ಯವನ್ನು ಕಂಡುಹಿಡಿಯಲು, ಸುತ್ತಳತೆಯನ್ನು 2π ಯಿಂದ ಭಾಗಿಸಿ, ನಾವು r = C / (2π) r = 18 ಅಡಿ / (2 * 3.14) r ≈ 18 ಅಡಿ / 6.28 r ≈ 2.87 ಅಡಿ (ಹತ್ತಿರದ ನೂರಕ್ಕೆ ದುಂಡಾದ) ಹೊಂದಿದ್ದೇವೆ.
ತ್ರಿಜ್ಯವನ್ನು ಕಂಡುಹಿಡಿಯಲು, ಸುತ್ತಳತೆಯನ್ನು 2π ಯಿಂದ ಭಾಗಿಸಿ, ನಾವು r = C / (2π) r = 18 ಅಡಿ / (2 * 3.14) r ≈ 18 ಅಡಿ / 6.28 r ≈ 2.87 ಅಡಿ (ಹತ್ತಿರದ ನೂರಕ್ಕೆ ದುಂಡಾದ) ಹೊಂದಿದ್ದೇವೆ.
![]() ಈಗ, ವ್ಯಾಸವನ್ನು ಕಂಡುಹಿಡಿಯಲು, ಸರಳವಾಗಿ ತ್ರಿಜ್ಯವನ್ನು ದ್ವಿಗುಣಗೊಳಿಸಿ: ವ್ಯಾಸ = 2 * ತ್ರಿಜ್ಯದ ವ್ಯಾಸ ≈ 2 * 2.87 ಅಡಿ ವ್ಯಾಸ ≈ 5.74 ಅಡಿ. ಆದ್ದರಿಂದ, ಪಿಕ್ನಿಕ್ ಟೇಬಲ್ ಸುಮಾರು 5.74 ಅಡಿ ವ್ಯಾಸವನ್ನು ಹೊಂದಿರಬೇಕು
ಈಗ, ವ್ಯಾಸವನ್ನು ಕಂಡುಹಿಡಿಯಲು, ಸರಳವಾಗಿ ತ್ರಿಜ್ಯವನ್ನು ದ್ವಿಗುಣಗೊಳಿಸಿ: ವ್ಯಾಸ = 2 * ತ್ರಿಜ್ಯದ ವ್ಯಾಸ ≈ 2 * 2.87 ಅಡಿ ವ್ಯಾಸ ≈ 5.74 ಅಡಿ. ಆದ್ದರಿಂದ, ಪಿಕ್ನಿಕ್ ಟೇಬಲ್ ಸುಮಾರು 5.74 ಅಡಿ ವ್ಯಾಸವನ್ನು ಹೊಂದಿರಬೇಕು
 ಕೀ ಟೇಕ್ಅವೇಗಳು
ಕೀ ಟೇಕ್ಅವೇಗಳು
![]() AhaSlides
AhaSlides ![]() ಶಿಕ್ಷಣ, ತರಬೇತಿ ಅಥವಾ ಮನರಂಜನಾ ಉದ್ದೇಶಗಳಿಗಾಗಿ ಟೋಪಿಯನ್ನು ಬಳಸಬಹುದಾದ ಅತ್ಯುತ್ತಮ ಸಂವಾದಾತ್ಮಕ ರಸಪ್ರಶ್ನೆ ತಯಾರಕ. ಪರಿಶೀಲಿಸಿ AhaSlides ಮುಕ್ತಗೊಳಿಸಲು ತಕ್ಷಣವೇ
ಶಿಕ್ಷಣ, ತರಬೇತಿ ಅಥವಾ ಮನರಂಜನಾ ಉದ್ದೇಶಗಳಿಗಾಗಿ ಟೋಪಿಯನ್ನು ಬಳಸಬಹುದಾದ ಅತ್ಯುತ್ತಮ ಸಂವಾದಾತ್ಮಕ ರಸಪ್ರಶ್ನೆ ತಯಾರಕ. ಪರಿಶೀಲಿಸಿ AhaSlides ಮುಕ್ತಗೊಳಿಸಲು ತಕ್ಷಣವೇ ![]() ಗ್ರಾಹಕೀಯಗೊಳಿಸಬಹುದಾದ ಟೆಂಪ್ಲೇಟ್ಗಳು
ಗ್ರಾಹಕೀಯಗೊಳಿಸಬಹುದಾದ ಟೆಂಪ್ಲೇಟ್ಗಳು![]() ಮತ್ತು ಸುಧಾರಿತ ವೈಶಿಷ್ಟ್ಯಗಳು!
ಮತ್ತು ಸುಧಾರಿತ ವೈಶಿಷ್ಟ್ಯಗಳು!
 ಪದೇ ಪದೇ ಕೇಳಲಾಗುವ ಪ್ರಶ್ನೆಗಳು
ಪದೇ ಪದೇ ಕೇಳಲಾಗುವ ಪ್ರಶ್ನೆಗಳು
![]() ವೃತ್ತದ 2πr ಎಂದರೇನು?
ವೃತ್ತದ 2πr ಎಂದರೇನು?
![]() 2πr ಎಂಬುದು ವೃತ್ತದ ಸುತ್ತಳತೆಯ ಸೂತ್ರವಾಗಿದೆ. ಈ ಸೂತ್ರದಲ್ಲಿ:
2πr ಎಂಬುದು ವೃತ್ತದ ಸುತ್ತಳತೆಯ ಸೂತ್ರವಾಗಿದೆ. ಈ ಸೂತ್ರದಲ್ಲಿ:
 "2" ನೀವು ತ್ರಿಜ್ಯದ ಎರಡು ಪಟ್ಟು ಉದ್ದವನ್ನು ತೆಗೆದುಕೊಳ್ಳುತ್ತಿರುವಿರಿ ಎಂದು ಪ್ರತಿನಿಧಿಸುತ್ತದೆ. ಸುತ್ತಳತೆಯು ವೃತ್ತದ ಸುತ್ತಲಿನ ಅಂತರವಾಗಿದೆ, ಆದ್ದರಿಂದ ನೀವು ಒಮ್ಮೆ ಮತ್ತು ನಂತರ ವೃತ್ತದ ಸುತ್ತಲೂ ಹೋಗಬೇಕು, ಅದಕ್ಕಾಗಿಯೇ ನಾವು 2 ರಿಂದ ಗುಣಿಸುತ್ತೇವೆ.
"2" ನೀವು ತ್ರಿಜ್ಯದ ಎರಡು ಪಟ್ಟು ಉದ್ದವನ್ನು ತೆಗೆದುಕೊಳ್ಳುತ್ತಿರುವಿರಿ ಎಂದು ಪ್ರತಿನಿಧಿಸುತ್ತದೆ. ಸುತ್ತಳತೆಯು ವೃತ್ತದ ಸುತ್ತಲಿನ ಅಂತರವಾಗಿದೆ, ಆದ್ದರಿಂದ ನೀವು ಒಮ್ಮೆ ಮತ್ತು ನಂತರ ವೃತ್ತದ ಸುತ್ತಲೂ ಹೋಗಬೇಕು, ಅದಕ್ಕಾಗಿಯೇ ನಾವು 2 ರಿಂದ ಗುಣಿಸುತ್ತೇವೆ. "π" (pi) ಒಂದು ಗಣಿತದ ಸ್ಥಿರಾಂಕವು ಸರಿಸುಮಾರು 3.14159 ಗೆ ಸಮಾನವಾಗಿರುತ್ತದೆ. ಇದನ್ನು ಬಳಸಲಾಗುತ್ತದೆ ಏಕೆಂದರೆ ಇದು ವೃತ್ತದ ಸುತ್ತಳತೆ ಮತ್ತು ವ್ಯಾಸದ ನಡುವಿನ ಸಂಬಂಧವನ್ನು ಪ್ರತಿನಿಧಿಸುತ್ತದೆ.
"π" (pi) ಒಂದು ಗಣಿತದ ಸ್ಥಿರಾಂಕವು ಸರಿಸುಮಾರು 3.14159 ಗೆ ಸಮಾನವಾಗಿರುತ್ತದೆ. ಇದನ್ನು ಬಳಸಲಾಗುತ್ತದೆ ಏಕೆಂದರೆ ಇದು ವೃತ್ತದ ಸುತ್ತಳತೆ ಮತ್ತು ವ್ಯಾಸದ ನಡುವಿನ ಸಂಬಂಧವನ್ನು ಪ್ರತಿನಿಧಿಸುತ್ತದೆ. "r" ವೃತ್ತದ ತ್ರಿಜ್ಯವನ್ನು ಪ್ರತಿನಿಧಿಸುತ್ತದೆ, ಇದು ವೃತ್ತದ ಮಧ್ಯಭಾಗದಿಂದ ಅದರ ಸುತ್ತಳತೆಯ ಯಾವುದೇ ಬಿಂದುವಿಗೆ ಇರುವ ಅಂತರವಾಗಿದೆ.
"r" ವೃತ್ತದ ತ್ರಿಜ್ಯವನ್ನು ಪ್ರತಿನಿಧಿಸುತ್ತದೆ, ಇದು ವೃತ್ತದ ಮಧ್ಯಭಾಗದಿಂದ ಅದರ ಸುತ್ತಳತೆಯ ಯಾವುದೇ ಬಿಂದುವಿಗೆ ಇರುವ ಅಂತರವಾಗಿದೆ.
![]() ಸುತ್ತಳತೆ ಏಕೆ 2πr ಆಗಿದೆ?
ಸುತ್ತಳತೆ ಏಕೆ 2πr ಆಗಿದೆ?
![]() ವೃತ್ತದ ಸುತ್ತಳತೆಯ ಸೂತ್ರ, C = 2πr, ಪೈ (π) ಮತ್ತು ವೃತ್ತದ ಜ್ಯಾಮಿತೀಯ ಗುಣಲಕ್ಷಣಗಳ ವ್ಯಾಖ್ಯಾನದಿಂದ ಬರುತ್ತದೆ. ಪೈ (π) ವೃತ್ತದ ಸುತ್ತಳತೆಯ ಅನುಪಾತವನ್ನು ಅದರ ವ್ಯಾಸಕ್ಕೆ ಪ್ರತಿನಿಧಿಸುತ್ತದೆ. ನೀವು ತ್ರಿಜ್ಯವನ್ನು (r) 2π ರಿಂದ ಗುಣಿಸಿದಾಗ, ನೀವು ಮೂಲಭೂತವಾಗಿ ವೃತ್ತದ ಸುತ್ತಲಿನ ಅಂತರವನ್ನು ಲೆಕ್ಕ ಹಾಕುತ್ತೀರಿ, ಇದು ಸುತ್ತಳತೆಯ ವ್ಯಾಖ್ಯಾನವಾಗಿದೆ.
ವೃತ್ತದ ಸುತ್ತಳತೆಯ ಸೂತ್ರ, C = 2πr, ಪೈ (π) ಮತ್ತು ವೃತ್ತದ ಜ್ಯಾಮಿತೀಯ ಗುಣಲಕ್ಷಣಗಳ ವ್ಯಾಖ್ಯಾನದಿಂದ ಬರುತ್ತದೆ. ಪೈ (π) ವೃತ್ತದ ಸುತ್ತಳತೆಯ ಅನುಪಾತವನ್ನು ಅದರ ವ್ಯಾಸಕ್ಕೆ ಪ್ರತಿನಿಧಿಸುತ್ತದೆ. ನೀವು ತ್ರಿಜ್ಯವನ್ನು (r) 2π ರಿಂದ ಗುಣಿಸಿದಾಗ, ನೀವು ಮೂಲಭೂತವಾಗಿ ವೃತ್ತದ ಸುತ್ತಲಿನ ಅಂತರವನ್ನು ಲೆಕ್ಕ ಹಾಕುತ್ತೀರಿ, ಇದು ಸುತ್ತಳತೆಯ ವ್ಯಾಖ್ಯಾನವಾಗಿದೆ.
![]() ಸುತ್ತಳತೆಯು ತ್ರಿಜ್ಯದ 3.14 ಪಟ್ಟು?
ಸುತ್ತಳತೆಯು ತ್ರಿಜ್ಯದ 3.14 ಪಟ್ಟು?
![]() ಇಲ್ಲ, ಸುತ್ತಳತೆಯು ನಿಖರವಾಗಿ ತ್ರಿಜ್ಯದ 3.14 ಪಟ್ಟು ಅಲ್ಲ. ವೃತ್ತದ ಸುತ್ತಳತೆ ಮತ್ತು ತ್ರಿಜ್ಯದ ನಡುವಿನ ಸಂಬಂಧವನ್ನು C = 2πr ಸೂತ್ರದಿಂದ ನೀಡಲಾಗಿದೆ. π (ಪೈ) ಸರಿಸುಮಾರು 3.14159 ಆಗಿದ್ದರೆ, ಸುತ್ತಳತೆಯು ತ್ರಿಜ್ಯದ 2 ಪಟ್ಟು π ಪಟ್ಟು ಇರುತ್ತದೆ. ಆದ್ದರಿಂದ, ಸುತ್ತಳತೆಯು ತ್ರಿಜ್ಯದ ಕೇವಲ 3.14 ಪಟ್ಟು ಹೆಚ್ಚು; ಇದು ತ್ರಿಜ್ಯದ 2 ಪಟ್ಟು π ಬಾರಿ.
ಇಲ್ಲ, ಸುತ್ತಳತೆಯು ನಿಖರವಾಗಿ ತ್ರಿಜ್ಯದ 3.14 ಪಟ್ಟು ಅಲ್ಲ. ವೃತ್ತದ ಸುತ್ತಳತೆ ಮತ್ತು ತ್ರಿಜ್ಯದ ನಡುವಿನ ಸಂಬಂಧವನ್ನು C = 2πr ಸೂತ್ರದಿಂದ ನೀಡಲಾಗಿದೆ. π (ಪೈ) ಸರಿಸುಮಾರು 3.14159 ಆಗಿದ್ದರೆ, ಸುತ್ತಳತೆಯು ತ್ರಿಜ್ಯದ 2 ಪಟ್ಟು π ಪಟ್ಟು ಇರುತ್ತದೆ. ಆದ್ದರಿಂದ, ಸುತ್ತಳತೆಯು ತ್ರಿಜ್ಯದ ಕೇವಲ 3.14 ಪಟ್ಟು ಹೆಚ್ಚು; ಇದು ತ್ರಿಜ್ಯದ 2 ಪಟ್ಟು π ಬಾರಿ.
![]() ಉಲ್ಲೇಖ:
ಉಲ್ಲೇಖ: ![]() ಓಮ್ನಿ ಕ್ಯಾಕ್ಯುಲೇಟರ್ |
ಓಮ್ನಿ ಕ್ಯಾಕ್ಯುಲೇಟರ್ | ![]() ಪ್ರೊ
ಪ್ರೊ







