ווי צו רעכענען די אַרומנעם פון אַ קרייַז פּונקט?
די אַרומנעם פון אַ קרייַז איז אַ יקערדיק און פארלאנגט מאטעמאטיק וויסן באַקענענ אין עלעמענטאַר אָדער מיטל שולע. מאַסטערינג די אַרומנעם פון אַ קרייַז איז יקערדיק פֿאַר סטודענטן וואָס פּלאַנירן צו נאָכגיין מער אַוואַנסירטע מאטעמאטיק קאָרסאַז אין מיטלשול און קאָלעגע און גרייטן זיך פֿאַר סטאַנדערדייזד יגזאַמז אַזאַ ווי SAT און ACT.
די 10 אַרומנעם פון אַ קרייַז קוויז אין דעם אַרטיקל איז דיזיינד צו פּרובירן דיין פארשטאנד פון דערגייונג די ראַדיוס, דיאַמעטער און אַרומנעם פון אַ קרייַז.
טיש פון אינהאַלט:
אַרומנעם פון אַ קרייַז פאָרמולע- אַרומנעם פון אַ קרייַז ויספרעג
- שליסל טייקאַווייַס
- אָפֿט געשטעלטע פֿראגן
אַרומנעם פון אַ קרייַז פאָרמולע
איידער איר נעמען אַ פּראָבע, לאָזן אונדז איבערחזרן עטלעכע קריטיש אינפֿאָרמאַציע!
ווי צו געפֿינען די אַרומנעם פון אַ קרייַזוואָס איז די אַרומנעם פון אַ קרייַז?
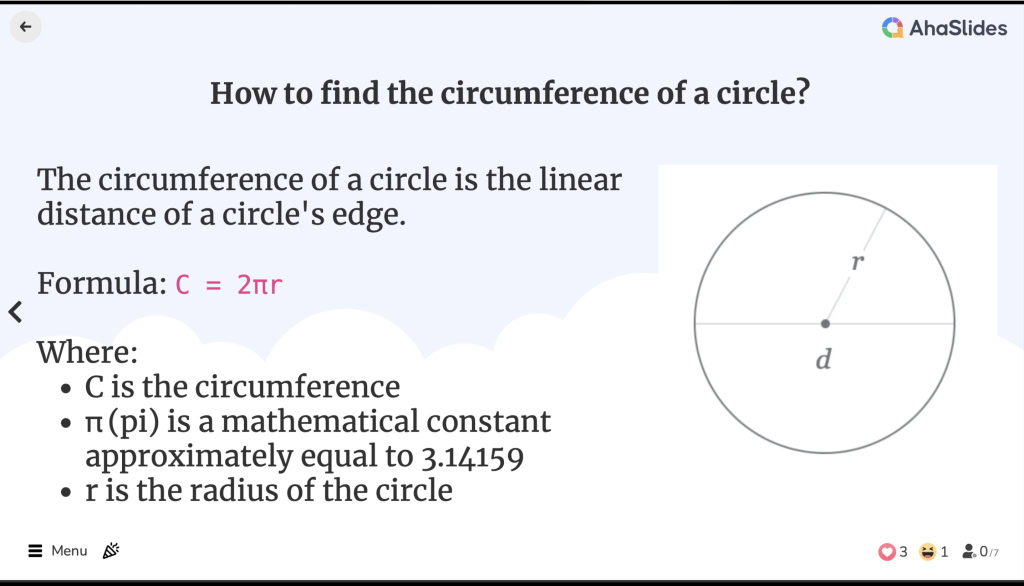
די אַרומנעם פון אַ קרייַז איז די לינעאַר דיסטאַנסע פון אַ קרייַז ס ברעג. עס איז עקוויוואַלענט צו די פּערימעטער פון אַ דזשיאַמעטריק פאָרעם, כאָטש דער טערמין פּערימעטער איז בלויז געניצט פֿאַר פּאָליגאָנס.
ווי צו געפֿינען די אַרומנעם פון אַ קרייַז?
די אַרומנעם פון אַ קרייַז פאָרמולע איז:
C = 2πr
ווו:
- C איז די אַרומנעם
- π (פּי) איז אַ מאַטאַמאַטיקאַל קעסיידערדיק בעערעך גלייַך צו 3.14159
- r איז דער ראַדיוס פון דעם קרייַז
דער ראַדיוס איז די ווייַטקייט פון דעם צענטער פון דעם קרייַז צו קיין פונט אויף דעם ברעג.
דער דיאַמעטער איז צוויי מאָל די ראַדיוס, אַזוי די אַרומנעם קענען אויך זיין אויסגעדריקט ווי:
C = πd
ווו:
- ד איז דער דיאַמעטער
פֿאַר בייַשפּיל, אויב די ראַדיוס פון אַ קרייַז איז 5 סענטימעטער, די אַרומנעם איז:
C = 2πr = 2π * 5 cm = 10π cm
≈ 31.4 סענטימעטער (ראַונדיד צו 2 דעצימאַל ערטער)
מער עצות פון AhaSlides
- 70+ מאַט קוויז פֿראגן פֿאַר שפּאַס עקסערסיסעס אין קלאַס
- 10 בעסטער קלאַסצימער מאַטהס גאַמעס פֿאַר באָרד ק12 סטודענטן
- 60 אָסאַם יידיאַז אויף מאַרך טעאַסערס פֿאַר אַדאַלץ | 2023 דערהייַנטיקונגען
AhaSlides איז די ולטימאַטע קוויז מאַקער
מאַכן ינטעראַקטיוו שפּילערייַ אין אַ רעגע מיט אונדזער ברייט מוסטער ביבליאָטעק צו טייטן באָרדאַם
אָנליין גאַמעס צו שפּילן ווען באָרדאַרומנעם פון אַ קרייַז ויספרעג
פראגע 1: אויב די אַרומנעם פון אַ קייַלעכיק שווימערייַ בעקן איז 50 מעטער, וואָס איז זייַן ראַדיוס?
א 7.95 מעטער
בי 8.00 מעטער
C. 15.91 מעטער
ד 25 מעטער
✅ ריכטיקע ענטפֿער:
א 7.95 מעטער
דערקלערונג:
די ראַדיוס קענען זיין געפֿונען דורך ריעריינדזשינג די פאָרמולע C = 2πr און סאַלווינג פֿאַר r: r = C / (2π). אויב איר פּלאַגינג די געגעבן אַרומנעם פון 50 מעטער און דערנענטערן π צו 3.14, מיר געפֿינען די ראַדיוס צו זיין בעערעך 7.95 מעטער.
פראגע 2: דער דיאַמעטער פון אַ קרייַז איז 14 אינטשעס. וואָס איז זייַן ראַדיוס?
א 28 אינטשעס
ב.14 אינטשעס
C. 21 אינטשעס
ד 7 אינטשעס
✅ ריכטיקע ענטפֿער:
ד 7 אינטשעס
דערקלערונג:
זינט דער דיאַמעטער איז צוויי מאָל די לענג פון די ראַדיוס (ד = 2 ר), איר קענען געפֿינען די ראַדיוס דורך דיוויידינג די דיאַמעטער דורך 2 (ר = ד / 2). אין דעם פאַל, דיוויידינג די געגעבן דיאַמעטער פון 14 אינטשעס דורך 2 גיט אַ ראַדיוס פון 7 אינטשעס.
געפינען די אַרומנעם פון אַ קרייַזפראגע 3: וואָס פון די פאלגענדע סטייטמאַנץ איז אמת וועגן די שייכות צווישן די דיאַמעטער און די אַרומנעם פון אַ קרייַז?
א. דער דיאַמעטער איז האַלב די אַרומנעם.
ב דער דיאַמעטער איז די זעלבע ווי די אַרומנעם.
C. דער דיאַמעטער איז צוויי מאָל די אַרומנעם.
ד דער דיאַמעטער איז π מאל די אַרומנעם.
✅ ריכטיקע ענטפֿער:
א. דער דיאַמעטער איז האַלב די אַרומנעם.
דערקלערונג:
דער דיאַמעטער איז גלייַך צו 2 מאל די ראַדיוס, בשעת די אַרומנעם איז גלייַך צו 2π מאל די ראַדיוס. דעריבער, דער דיאַמעטער איז האַלב די אַרומנעם.
פראגע 4: דער טיש וואָס מיר האָבן צו זיצן בייַ האט אַ אַרומנעם פון 6.28 יאַרדס. מיר דאַרפֿן צו געפֿינען די דיאַמעטער פון די טיש.
א 1 הויף
ב 2 יאַרדס
ג 3 יאַרדס
ד 4 יאַרדס
✅ ריכטיקע ענטפֿער:
ב 2 יאַרדס
דערקלערונג:
די אַרומנעם פון אַ קרייַז איז קאַלקיאַלייטיד דורך מערן דעם דיאַמעטער מיט פּי (π). אין דעם פאַל, די אַרומנעם איז 6.28 יאַרדס. צו געפֿינען די דיאַמעטער, מיר דאַרפֿן צו טיילן די אַרומנעם דורך פּי. דיוויידינג 6.28 יאַרדס דורך פּי גיט אונדז בעערעך 2 יאַרדס. דעריבער, דער דיאַמעטער פון די טיש איז 2 יאַרדס.
פראגע 5: א צירקולאר גארטן האט א ארומנעם פון 36 מעטער. וואָס איז דער דערנענטערנ ראַדיוס פון דעם גאָרטן?
א 3.14 מעטער
בי 6 מעטער
C. 9 מעטער
ד 18 מעטער
✅ ריכטיקע ענטפֿער:
C. 9 מעטער
דערקלערונג:
צו געפֿינען די ראַדיוס, נוצן די פאָרמולע פֿאַר אַרומנעם: C = 2πr. ריעריינדזש די פאָרמולע צו סאָלווע פֿאַר די ראַדיוס: r = C / (2π). פּלאַגינג אין די געגעבן אַרומנעם פון 36 מעטער און ניצן אַ דערנענטערנ ווערט פון π ווי 3.14, איר באַקומען ר = 36 / (2 * 3.14) ≈ 9 מעטער.
פראגע 6: א קייַלעכיק שווימערייַ בעקן האט אַ ראַדיוס פון 8 מעטער. וואָס איז די דערנענטערנ ווייַטקייט אַ שווימער טראַוואַלז אַרום די בעקן ווען קאַמפּליטינג איין שויס?
א 16 מעטער
בי 25 מעטער
C. 50 מעטער
ד 100 מעטער
✅ ריכטיקע ענטפֿער:
C. 50 מעטער
דערקלערונג:
צו געפֿינען די ווייַטקייט אַ שווימער טראַוואַלז אַרום די בעקן פֿאַר איין שויס, איר נוצן די אַרומנעם פאָרמולע (C = 2πr). אין דעם פאַל, עס איז 2 * 3.14 * 8 מעטער ≈ 50.24 מעטער, וואָס איז בעערעך 50 מעטער.
פראגע 7: ווען מעסטן די כולאַ רייַף אין קלאַס, גרופּע C דיסקאַווערד אַז עס האט אַ ראַדיוס פון 7 אינטשעס. וואָס איז די אַרומנעם פון די כולאַ רייַף?
א 39.6 אינטשעס
ב 37.6 אינטשעס
C. 47.6 אינטשעס
ד 49.6 אינטשעס
✅ ריכטיקע ענטפֿער:
C. 47.6 אינטשעס
דערקלערונג:
די אַרומנעם פון אַ קרייַז קענען זיין געפֿונען מיט די פאָרמולע C = 2πr, ווו r איז דער ראַדיוס פון דעם קרייַז. אין דעם פאַל, די ראַדיוס פון די כולאַ רייַף איז געגעבן ווי 7 אינטשעס. פּלאַגינג דעם ווערט אין די פאָרמולע, מיר באַקומען C = 2π (7) = 14π אינטשעס. דערנענטערנ זיך π צו 3.14, מיר קענען רעכענען די אַרומנעם ווי 14 (3.14) = 43.96 אינטשעס. ראַונדיד צו די ניראַסט צענט, די אַרומנעם איז 47.6 אינטשעס, וואָס שוועבעלעך די געגעבן ענטפער.
פראגע 8: א האלבצירקל האט א ראדיוס פון 10 מעטער. וואָס איז זייַן פּערימעטער?
א 20 מעטער
בי 15 מעטער
C. 31.42 מעטער
ד 62.84 מעטער
✅ ריכטיקע ענטפֿער:
C. 31.42 מעטער
דערקלערונג:צו געפֿינען די פּערימעטער פון די האַלב-סירקלע, רעכענען האַלב די אַרומנעם פון אַ גאַנץ קרייַז מיט אַ ראַדיוס פון 10 מעטער.
אַרומנעם פון אַ קרייַז בייַשפּילפראגע 9: די קוישבאָל מאַנשאַפֿט שפּילט מיט אַ פּילקע מיט אַ ראַדיוס פון 5.6 אינטשעס. וואָס איז די אַרומנעם פון יעדער קוישבאָל?
א 11.2 אינטשעס
ב 17.6 אינטשעס
C. 22.4 אינטשעס
ד 35.2 אינטשעס
✅ ריכטיקע ענטפֿער:
C. 22.4 אינטשעס
דערקלערונג:
איר קענען נוצן די פאָרמולע פֿאַר די אַרומנעם פון אַ קרייַז, וואָס איז C = 2πr. די געגעבן ראַדיוס איז 5.6 אינטשעס. צאַפּן דעם ווערט אין די פאָרמולע, מיר האָבן C = 2π * 5.6 אינטשעס. C ≈ 2 * 3.14 * 5.6 אינטשעס. C ≈ 11.2 * 5.6 אינטשעס. C ≈ 22.4 אינטשעס. אַזוי, די אַרומנעם פון יעדער קוישבאָל איז בעערעך 22.4 אינטשעס. דאָס רעפּראַזענץ די ווייַטקייט אַרום די קוישבאָל.
פראגע 10: שרה און איר צוויי פריינט האָבן געבויט אַ קייַלעכיק מאַכנ אַ פּיקניק טיש פֿאַר זייער צונויפקום. ז ײ האב ן געוװסט , א ז כד י ז ײ זאל ן זי ך אל ע בא ־ קוועם ט זיצ ן ארו ם טיש , דארפ ן ז ײ א ארומיק ן פו ן 18 פיס . וואָס דיאַמעטער מוזן האָבן די מאַכנ אַ פּיקניק טיש צו דערגרייכן די ריכטיק אַרומנעם?
א 3 פֿיס
ב 6 פֿיס
ג 9 פֿיס
ד 12 פוס
✅ ריכטיקע ענטפֿער:
ב 6 פֿיס
דערקלערונג:
צו געפֿינען דעם ראַדיוס, טיילן די אַרומנעם מיט 2π, מיר האָבן r = C / (2π) r = 18 פֿיס / (2 * 3.14) ר ≈ 18 פֿיס / 6.28 ר ≈ 2.87 פֿיס (ראַונדיד צו די ניראַסט הונדערטסט).
איצט, צו געפֿינען דעם דיאַמעטער, פשוט טאָפּל די ראַדיוס: דיאַמעטער = 2 * ראַדיוס דיאַמעטער ≈ 2 * 2.87 פֿיס דיאַמעטער ≈ 5.74 פֿיס. אַזוי, די מאַכנ אַ פּיקניק טיש מוזן האָבן אַ דיאַמעטער פון בעערעך 5.74 פֿיס
שליסל טייקאַווייַס
AhaSlides איז דער בעסטער ינטעראַקטיוו ויספרעג פאַבריקאַנט אַז הוט קענען זיין געוויינט פֿאַר בילדונג, טריינינג אָדער פאַרווייַלונג צוועקן. טשעק אויס AhaSlides גלייך צו באַקומען פריי קוסטאָמיזאַבלע טעמפּלאַטעסאון אַוואַנסירטע פֿעיִקייטן!
אָפֿט געשטעלטע פֿראגן
וואָס איז 2πr פון אַ קרייַז?
2πr איז די פאָרמולע פֿאַר די אַרומנעם פון אַ קרייַז. אין דעם פאָרמולע:
- "2" רעפּראַזענץ אַז איר נעמען צוויי מאָל די לענג פון די ראַדיוס. די אַרומנעם איז די דיסטאַנסע אַרום דעם קרייַז, אַזוי איר דאַרפֿן צו גיין אַרום דעם קרייַז אַמאָל און דעמאָלט ווידער, וואָס איז וואָס מיר מערן מיט 2.
- "π" (פּי) איז אַ מאַטאַמאַטיקאַל קעסיידערדיק בעערעך גלייַך צו 3.14159. עס איז געניצט ווייַל עס רעפּראַזענץ די שייכות צווישן די אַרומנעם און די דיאַמעטער פון אַ קרייַז.
- "ר" רעפּראַזענץ די ראַדיוס פון דעם קרייַז, וואָס איז די ווייַטקייט פון דעם צענטער פון דעם קרייַז צו קיין פונט אויף זייַן אַרומנעם.
פארוואס איז די אַרומנעם 2πr?
די פאָרמולע פֿאַר די אַרומנעם פון אַ קרייַז, C = 2πr, קומט פון די דעפֿיניציע פון פּי (π) און די דזשיאַמעטריק פּראָפּערטיעס פון אַ קרייַז. פּי (π) רעפּראַזענץ די פאַרהעלטעניש פון די אַרומנעם פון אַ קרייַז צו זייַן דיאַמעטער. ווען איר מערן די ראַדיוס (ר) מיט 2π, איר יסענשאַלי רעכענען די ווייַטקייט אַרום דעם קרייַז, וואָס איז די דעפֿיניציע פון אַרומנעם.
איז די אַרומנעם 3.14 מאל די ראַדיוס?
ניין, די אַרומנעם איז נישט פּונקט 3.14 מאל די ראַדיוס. די שייכות צווישן די אַרומנעם און די ראַדיוס פון אַ קרייַז איז געגעבן דורך די פאָרמולע C = 2πr. בשעת π (פּי) איז בעערעך 3.14159, די אַרומנעם איז 2 מאל π מאל די ראַדיוס. אַזוי, די אַרומנעם איז מער ווי בלויז 3.14 מאל די ראַדיוס; עס איז 2 מאל π מאל די ראַדיוס.
Ref: אָמני קאַקולאַטאָר | פּראָפ
טאַגס: קוויז געדאַנק
