![]() किसी वृत्त की परिधि की सटीक गणना कैसे करें?
किसी वृत्त की परिधि की सटीक गणना कैसे करें?
![]() वृत्त की परिधि प्राथमिक या मध्य विद्यालय में शुरू किया गया एक बुनियादी और आवश्यक गणित ज्ञान है। वृत्त की परिधि में महारत हासिल करना उन छात्रों के लिए आवश्यक है जो हाई स्कूल और कॉलेज में अधिक उन्नत गणित पाठ्यक्रमों को आगे बढ़ाने और SAT और ACT जैसी मानकीकृत परीक्षाओं की तैयारी करने की योजना बनाते हैं।
वृत्त की परिधि प्राथमिक या मध्य विद्यालय में शुरू किया गया एक बुनियादी और आवश्यक गणित ज्ञान है। वृत्त की परिधि में महारत हासिल करना उन छात्रों के लिए आवश्यक है जो हाई स्कूल और कॉलेज में अधिक उन्नत गणित पाठ्यक्रमों को आगे बढ़ाने और SAT और ACT जैसी मानकीकृत परीक्षाओं की तैयारी करने की योजना बनाते हैं।
![]() इस लेख में वृत्त की 10 परिधि प्रश्नोत्तरी एक वृत्त की त्रिज्या, व्यास और परिधि को खोजने की आपकी समझ का परीक्षण करने के लिए डिज़ाइन की गई है।
इस लेख में वृत्त की 10 परिधि प्रश्नोत्तरी एक वृत्त की त्रिज्या, व्यास और परिधि को खोजने की आपकी समझ का परीक्षण करने के लिए डिज़ाइन की गई है।
![]() सामग्री की तालिका:
सामग्री की तालिका:
 एक वृत्त सूत्र की परिधि
एक वृत्त सूत्र की परिधि
![]() परीक्षा देने से पहले, आइए कुछ महत्वपूर्ण जानकारी पुनः याद कर लें!
परीक्षा देने से पहले, आइए कुछ महत्वपूर्ण जानकारी पुनः याद कर लें!
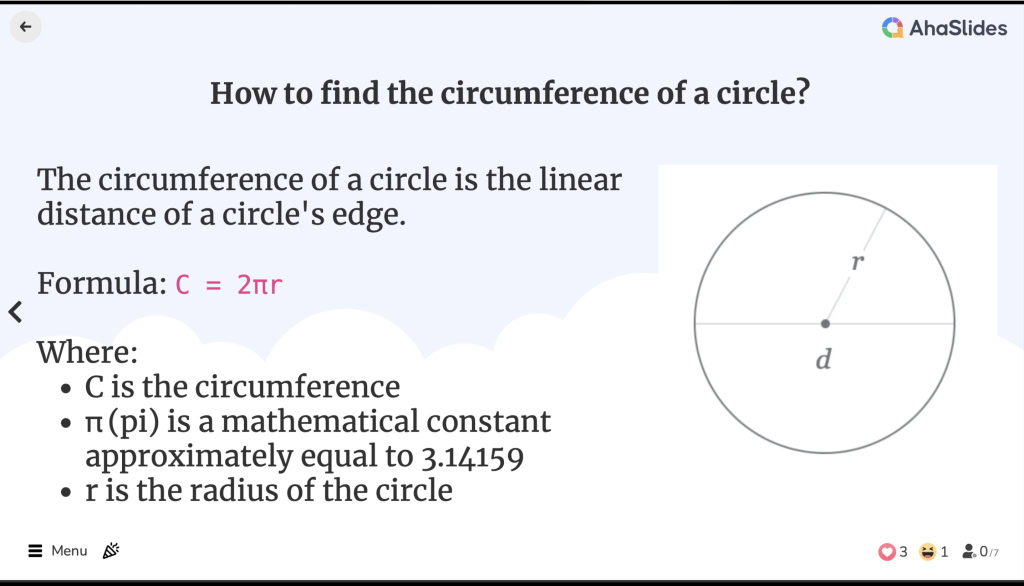
 वृत्त की परिधि कैसे ज्ञात करें
वृत्त की परिधि कैसे ज्ञात करें![]() वृत्त की परिधि क्या है?
वृत्त की परिधि क्या है?
![]() किसी वृत्त की परिधि, वृत्त के किनारे की रैखिक दूरी होती है। यह ज्यामितीय आकार की परिधि के बराबर होती है, हालाँकि परिधि शब्द का इस्तेमाल सिर्फ़ बहुभुजों के लिए किया जाता है।
किसी वृत्त की परिधि, वृत्त के किनारे की रैखिक दूरी होती है। यह ज्यामितीय आकार की परिधि के बराबर होती है, हालाँकि परिधि शब्द का इस्तेमाल सिर्फ़ बहुभुजों के लिए किया जाता है।
![]() वृत्त की परिधि कैसे ज्ञात करें?
वृत्त की परिधि कैसे ज्ञात करें?
![]() वृत्त की परिधि का सूत्र है:
वृत्त की परिधि का सूत्र है:
C = 2πr
![]() जहाँ:
जहाँ:
 C परिधि है
C परिधि है π (pi) एक गणितीय स्थिरांक है जो लगभग 3.14159 के बराबर है
π (pi) एक गणितीय स्थिरांक है जो लगभग 3.14159 के बराबर है r वृत्त की त्रिज्या है
r वृत्त की त्रिज्या है
![]() त्रिज्या वृत्त के केंद्र से किनारे पर किसी बिंदु तक की दूरी है।
त्रिज्या वृत्त के केंद्र से किनारे पर किसी बिंदु तक की दूरी है।
![]() व्यास त्रिज्या का दोगुना है, इसलिए परिधि को इस प्रकार भी व्यक्त किया जा सकता है:
व्यास त्रिज्या का दोगुना है, इसलिए परिधि को इस प्रकार भी व्यक्त किया जा सकता है:
C = πd
![]() जहाँ:
जहाँ:
 d व्यास है
d व्यास है
![]() उदाहरण के लिए, यदि किसी वृत्त की त्रिज्या 5 सेमी है, तो परिधि है:
उदाहरण के लिए, यदि किसी वृत्त की त्रिज्या 5 सेमी है, तो परिधि है:
C = 2πr = 2π * 5 cm = 10π cm
![]() ≈ 31.4 सेमी (2 दशमलव स्थानों तक गोलाकार)
≈ 31.4 सेमी (2 दशमलव स्थानों तक गोलाकार)
 अधिक सुझाव AhaSlides
अधिक सुझाव AhaSlides
 कक्षा में मज़ा अभ्यास के लिए 70+ गणित प्रश्नोत्तरी प्रश्न
कक्षा में मज़ा अभ्यास के लिए 70+ गणित प्रश्नोत्तरी प्रश्न ऊब गए K10 छात्रों के लिए 12 सर्वश्रेष्ठ कक्षा गणित खेल
ऊब गए K10 छात्रों के लिए 12 सर्वश्रेष्ठ कक्षा गणित खेल वयस्कों के लिए ब्रेन टीज़र पर 60 अद्भुत विचार | 2023 अपडेट
वयस्कों के लिए ब्रेन टीज़र पर 60 अद्भुत विचार | 2023 अपडेट
![]() AhaSlides सर्वश्रेष्ठ क्विज़ निर्माता है
AhaSlides सर्वश्रेष्ठ क्विज़ निर्माता है
![]() बोरियत दूर करने के लिए हमारी व्यापक टेम्पलेट लाइब्रेरी के साथ तुरंत इंटरैक्टिव गेम बनाएं
बोरियत दूर करने के लिए हमारी व्यापक टेम्पलेट लाइब्रेरी के साथ तुरंत इंटरैक्टिव गेम बनाएं

 बोर होने पर खेलने के लिए ऑनलाइन गेम
बोर होने पर खेलने के लिए ऑनलाइन गेम वृत्त प्रश्नोत्तरी की परिधि
वृत्त प्रश्नोत्तरी की परिधि
![]() प्रश्न 1: यदि एक गोलाकार स्विमिंग पूल की परिधि 50 मीटर है, तो इसकी त्रिज्या क्या है?
प्रश्न 1: यदि एक गोलाकार स्विमिंग पूल की परिधि 50 मीटर है, तो इसकी त्रिज्या क्या है?
![]() उ. 7.95 मीटर
उ. 7.95 मीटर
![]() बी. 8.00 मीटर
बी. 8.00 मीटर
![]() सी. 15.91 मीटर
सी. 15.91 मीटर
![]() डी. 25 मीटर
डी. 25 मीटर
✅ ![]() सही जवाब:
सही जवाब:
![]() उ. 7.95 मीटर
उ. 7.95 मीटर
![]() स्पष्टीकरण:
स्पष्टीकरण:
![]() त्रिज्या को सूत्र C = 2πr को पुनर्व्यवस्थित करके और r के लिए हल करके पाया जा सकता है: r = C / (2π)। 50 मीटर की दी गई परिधि को जोड़ने और π से 3.14 का अनुमान लगाने पर, हम त्रिज्या लगभग 7.95 मीटर पाते हैं।
त्रिज्या को सूत्र C = 2πr को पुनर्व्यवस्थित करके और r के लिए हल करके पाया जा सकता है: r = C / (2π)। 50 मीटर की दी गई परिधि को जोड़ने और π से 3.14 का अनुमान लगाने पर, हम त्रिज्या लगभग 7.95 मीटर पाते हैं।
![]() प्रश्न 2: एक वृत्त का व्यास 14 इंच है। इसकी त्रिज्या क्या है?
प्रश्न 2: एक वृत्त का व्यास 14 इंच है। इसकी त्रिज्या क्या है?
![]() उ. 28 इंच
उ. 28 इंच
![]() बी.14 इंच
बी.14 इंच
![]() सी. 21 इंच
सी. 21 इंच
![]() डी. 7 इंच
डी. 7 इंच
✅ ![]() सही जवाब:
सही जवाब:
![]() डी. 7 इंच
डी. 7 इंच
![]() स्पष्टीकरण:
स्पष्टीकरण:
![]() चूँकि व्यास त्रिज्या (d = 2r) की लंबाई का दोगुना है, आप व्यास को 2 (r = d / 2) से विभाजित करके त्रिज्या पा सकते हैं। इस मामले में, 14 इंच के दिए गए व्यास को 2 से विभाजित करने पर a प्राप्त होता है 7 इंच की त्रिज्या.
चूँकि व्यास त्रिज्या (d = 2r) की लंबाई का दोगुना है, आप व्यास को 2 (r = d / 2) से विभाजित करके त्रिज्या पा सकते हैं। इस मामले में, 14 इंच के दिए गए व्यास को 2 से विभाजित करने पर a प्राप्त होता है 7 इंच की त्रिज्या.

 एक वृत्त की परिधि ज्ञात कीजिए
एक वृत्त की परिधि ज्ञात कीजिए![]() प्रश्न 3: वृत्त के व्यास और परिधि के बीच संबंध के बारे में निम्नलिखित में से कौन सा कथन सत्य है?
प्रश्न 3: वृत्त के व्यास और परिधि के बीच संबंध के बारे में निम्नलिखित में से कौन सा कथन सत्य है?
![]() A. व्यास परिधि का आधा है।
A. व्यास परिधि का आधा है।
![]() B. व्यास परिधि के समान है।
B. व्यास परिधि के समान है।
![]() C. व्यास परिधि का दोगुना है।
C. व्यास परिधि का दोगुना है।
![]() D. व्यास परिधि का π गुना है।
D. व्यास परिधि का π गुना है।
✅ ![]() सही जवाब:
सही जवाब:
![]() A. व्यास परिधि का आधा है।
A. व्यास परिधि का आधा है।
![]() स्पष्टीकरण:
स्पष्टीकरण:
![]() व्यास त्रिज्या के 2 गुना के बराबर है, जबकि परिधि त्रिज्या के 2π गुना के बराबर है। इसलिए, व्यास परिधि का आधा है।
व्यास त्रिज्या के 2 गुना के बराबर है, जबकि परिधि त्रिज्या के 2π गुना के बराबर है। इसलिए, व्यास परिधि का आधा है।
![]() प्रश्न 4: जिस मेज़ पर हमें बैठना है उसकी परिधि 6.28 गज है। हमें मेज का व्यास ज्ञात करना होगा।
प्रश्न 4: जिस मेज़ पर हमें बैठना है उसकी परिधि 6.28 गज है। हमें मेज का व्यास ज्ञात करना होगा।
![]() ए. 1 गज
ए. 1 गज
![]() बी. 2 गज
बी. 2 गज
![]() सी. 3 गज
सी. 3 गज
![]() डी. 4 गज
डी. 4 गज
✅ ![]() सही जवाब:
सही जवाब:
![]() बी. 2 गज
बी. 2 गज
![]() स्पष्टीकरण:
स्पष्टीकरण:
![]() किसी वृत्त की परिधि की गणना व्यास को पाई (π) से गुणा करके की जाती है। इस मामले में, परिधि 6.28 गज दी गई है। व्यास ज्ञात करने के लिए, हमें परिधि को पाई से विभाजित करना होगा। 6.28 गज को पाई से विभाजित करने पर हमें लगभग 2 गज प्राप्त होता है। अतः मेज़ का व्यास 2 गज है।
किसी वृत्त की परिधि की गणना व्यास को पाई (π) से गुणा करके की जाती है। इस मामले में, परिधि 6.28 गज दी गई है। व्यास ज्ञात करने के लिए, हमें परिधि को पाई से विभाजित करना होगा। 6.28 गज को पाई से विभाजित करने पर हमें लगभग 2 गज प्राप्त होता है। अतः मेज़ का व्यास 2 गज है।
![]() प्रश्न 5: एक वृत्ताकार उद्यान की परिधि 36 मीटर है। बगीचे की अनुमानित त्रिज्या क्या है?
प्रश्न 5: एक वृत्ताकार उद्यान की परिधि 36 मीटर है। बगीचे की अनुमानित त्रिज्या क्या है?
![]() उ. 3.14 मीटर
उ. 3.14 मीटर
![]() बी. 6 मीटर
बी. 6 मीटर
![]() सी. 9 मीटर
सी. 9 मीटर
![]() डी. 18 मीटर
डी. 18 मीटर
✅ ![]() सही जवाब:
सही जवाब:
![]() सी. 9 मीटर
सी. 9 मीटर
![]() स्पष्टीकरण:
स्पष्टीकरण:
![]() त्रिज्या ज्ञात करने के लिए, परिधि के सूत्र का उपयोग करें: C = 2πr. त्रिज्या को हल करने के लिए सूत्र को पुनर्व्यवस्थित करें: r = C / (2π)। 36 मीटर की दी गई परिधि को जोड़ने और π के अनुमानित मान को 3.14 के रूप में उपयोग करने पर, आपको r = 36 / (2 * 3.14) ≈ 9 मीटर मिलता है।
त्रिज्या ज्ञात करने के लिए, परिधि के सूत्र का उपयोग करें: C = 2πr. त्रिज्या को हल करने के लिए सूत्र को पुनर्व्यवस्थित करें: r = C / (2π)। 36 मीटर की दी गई परिधि को जोड़ने और π के अनुमानित मान को 3.14 के रूप में उपयोग करने पर, आपको r = 36 / (2 * 3.14) ≈ 9 मीटर मिलता है।
![]() प्रश्न 6: एक गोलाकार स्विमिंग पूल की त्रिज्या 8 मीटर है। एक चक्कर पूरा करते समय एक तैराक पूल के चारों ओर लगभग कितनी दूरी तय करता है?
प्रश्न 6: एक गोलाकार स्विमिंग पूल की त्रिज्या 8 मीटर है। एक चक्कर पूरा करते समय एक तैराक पूल के चारों ओर लगभग कितनी दूरी तय करता है?
![]() उ. 16 मीटर
उ. 16 मीटर
![]() बी. 25 मीटर
बी. 25 मीटर
![]() सी. 50 मीटर
सी. 50 मीटर
![]() डी. 100 मीटर
डी. 100 मीटर
✅ ![]() सही जवाब:
सही जवाब:
![]() सी. 50 मीटर
सी. 50 मीटर
![]() स्पष्टीकरण:
स्पष्टीकरण:
![]() एक चक्कर में तैराक द्वारा पूल के चारों ओर तय की गई दूरी का पता लगाने के लिए, आप परिधि सूत्र (C = 2πr) का उपयोग करते हैं। इस मामले में, यह 2 * 3.14 * 8 मीटर ≈ 50.24 मीटर है, जो लगभग 50 मीटर है।
एक चक्कर में तैराक द्वारा पूल के चारों ओर तय की गई दूरी का पता लगाने के लिए, आप परिधि सूत्र (C = 2πr) का उपयोग करते हैं। इस मामले में, यह 2 * 3.14 * 8 मीटर ≈ 50.24 मीटर है, जो लगभग 50 मीटर है।
![]() प्रश्न 7: कक्षा में हुला हूप को मापते समय, समूह सी ने पाया कि इसकी त्रिज्या 7 इंच थी। हुला हूप की परिधि क्या है?
प्रश्न 7: कक्षा में हुला हूप को मापते समय, समूह सी ने पाया कि इसकी त्रिज्या 7 इंच थी। हुला हूप की परिधि क्या है?
![]() उ. 39.6 इंच
उ. 39.6 इंच
![]() बी. 37.6 इंच
बी. 37.6 इंच
![]() सी. 47.6 इंच
सी. 47.6 इंच
![]() डी. 49.6 इंच
डी. 49.6 इंच
✅ ![]() सही जवाब:
सही जवाब:
![]() सी. 47.6 इंच
सी. 47.6 इंच
![]() स्पष्टीकरण:
स्पष्टीकरण:
![]() एक वृत्त की परिधि सूत्र C = 2πr का उपयोग करके पाई जा सकती है, जहाँ r वृत्त की त्रिज्या है। इस मामले में, हुला हूप की त्रिज्या 7 इंच दी गई है। इस मान को सूत्र में जोड़ने पर, हमें C = 2π(7) = 14π इंच मिलता है। π से 3.14 का अनुमान लगाते हुए, हम परिधि की गणना 14(3.14) = 43.96 इंच के रूप में कर सकते हैं। निकटतम दसवें तक पूर्णांकित, परिधि 47.6 इंच है, जो दिए गए उत्तर से मेल खाती है।
एक वृत्त की परिधि सूत्र C = 2πr का उपयोग करके पाई जा सकती है, जहाँ r वृत्त की त्रिज्या है। इस मामले में, हुला हूप की त्रिज्या 7 इंच दी गई है। इस मान को सूत्र में जोड़ने पर, हमें C = 2π(7) = 14π इंच मिलता है। π से 3.14 का अनुमान लगाते हुए, हम परिधि की गणना 14(3.14) = 43.96 इंच के रूप में कर सकते हैं। निकटतम दसवें तक पूर्णांकित, परिधि 47.6 इंच है, जो दिए गए उत्तर से मेल खाती है।
![]() प्रश्न 8: एक अर्धवृत्त की त्रिज्या 10 मीटर है। इसकी परिधि क्या है?
प्रश्न 8: एक अर्धवृत्त की त्रिज्या 10 मीटर है। इसकी परिधि क्या है?
![]() उ. 20 मीटर
उ. 20 मीटर
![]() बी. 15 मीटर
बी. 15 मीटर
![]() सी. 31.42 मीटर
सी. 31.42 मीटर
![]() डी. 62.84 मीटर
डी. 62.84 मीटर
✅ ![]() सही जवाब:
सही जवाब:
![]() सी. 31.42 मीटर
सी. 31.42 मीटर
![]() स्पष्टीकरण:
स्पष्टीकरण:![]() अर्धवृत्त की परिधि ज्ञात करने के लिए, 10 मीटर त्रिज्या वाले पूर्ण वृत्त की आधी परिधि की गणना करें।
अर्धवृत्त की परिधि ज्ञात करने के लिए, 10 मीटर त्रिज्या वाले पूर्ण वृत्त की आधी परिधि की गणना करें।

 एक वृत्त की परिधि का उदाहरण
एक वृत्त की परिधि का उदाहरण![]() प्रश्न 9: बास्केटबॉल टीम 5.6 इंच त्रिज्या वाली गेंद से खेलती है। प्रत्येक बास्केटबॉल की परिधि क्या है?
प्रश्न 9: बास्केटबॉल टीम 5.6 इंच त्रिज्या वाली गेंद से खेलती है। प्रत्येक बास्केटबॉल की परिधि क्या है?
![]() उ. 11.2 इंच
उ. 11.2 इंच
![]() बी. 17.6 इंच
बी. 17.6 इंच
![]() सी. 22.4 इंच
सी. 22.4 इंच
![]() डी. 35.2 इंच
डी. 35.2 इंच
✅ ![]() सही जवाब:
सही जवाब:
![]() सी. 22.4 इंच
सी. 22.4 इंच
![]() व्याख्या:
व्याख्या:
![]() आप किसी वृत्त की परिधि के लिए सूत्र का उपयोग कर सकते हैं, जो C = 2πr है। दी गई त्रिज्या 5.6 इंच है। इस मान को सूत्र में जोड़ें, हमारे पास C = 2π * 5.6 इंच है। सी ≈ 2 * 3.14 * 5.6 इंच। सी ≈ 11.2 * 5.6 इंच। सी ≈ 22.4 इंच. तो, प्रत्येक बास्केटबॉल की परिधि लगभग 22.4 इंच है। यह बास्केटबॉल के चारों ओर की दूरी को दर्शाता है।
आप किसी वृत्त की परिधि के लिए सूत्र का उपयोग कर सकते हैं, जो C = 2πr है। दी गई त्रिज्या 5.6 इंच है। इस मान को सूत्र में जोड़ें, हमारे पास C = 2π * 5.6 इंच है। सी ≈ 2 * 3.14 * 5.6 इंच। सी ≈ 11.2 * 5.6 इंच। सी ≈ 22.4 इंच. तो, प्रत्येक बास्केटबॉल की परिधि लगभग 22.4 इंच है। यह बास्केटबॉल के चारों ओर की दूरी को दर्शाता है।
![]() प्रश्न 10: सारा और उसकी दो सहेलियाँ अपनी सभा के लिए एक गोलाकार पिकनिक टेबल बना रही थीं। वे जानते थे कि उन सभी को मेज के चारों ओर आराम से बैठने के लिए 18 फीट की परिधि की आवश्यकता है। सही परिधि प्राप्त करने के लिए पिकनिक टेबल का व्यास कितना होना चाहिए?
प्रश्न 10: सारा और उसकी दो सहेलियाँ अपनी सभा के लिए एक गोलाकार पिकनिक टेबल बना रही थीं। वे जानते थे कि उन सभी को मेज के चारों ओर आराम से बैठने के लिए 18 फीट की परिधि की आवश्यकता है। सही परिधि प्राप्त करने के लिए पिकनिक टेबल का व्यास कितना होना चाहिए?
![]() उ. 3 फीट
उ. 3 फीट
![]() बी. 6 फीट
बी. 6 फीट
![]() सी. 9 फीट
सी. 9 फीट
![]() डी. 12 फीट
डी. 12 फीट
✅ ![]() सही जवाब:
सही जवाब:
![]() बी. 6 फीट
बी. 6 फीट
![]() स्पष्टीकरण:
स्पष्टीकरण:
![]() त्रिज्या ज्ञात करने के लिए, परिधि को 2π से विभाजित करें, हमारे पास r = C / (2π) r = 18 फीट / (2 * 3.14) r ≈ 18 फीट / 6.28 r ≈ 2.87 फीट (निकटतम सौवें तक पूर्णांकित) है।
त्रिज्या ज्ञात करने के लिए, परिधि को 2π से विभाजित करें, हमारे पास r = C / (2π) r = 18 फीट / (2 * 3.14) r ≈ 18 फीट / 6.28 r ≈ 2.87 फीट (निकटतम सौवें तक पूर्णांकित) है।
![]() अब, व्यास ज्ञात करने के लिए, बस त्रिज्या को दोगुना करें: व्यास = 2 * त्रिज्या व्यास ≈ 2 * 2.87 फीट व्यास ≈ 5.74 फीट। तो, पिकनिक टेबल का व्यास लगभग 5.74 फीट होना चाहिए
अब, व्यास ज्ञात करने के लिए, बस त्रिज्या को दोगुना करें: व्यास = 2 * त्रिज्या व्यास ≈ 2 * 2.87 फीट व्यास ≈ 5.74 फीट। तो, पिकनिक टेबल का व्यास लगभग 5.74 फीट होना चाहिए
 चाबी छीन लेना
चाबी छीन लेना
![]() AhaSlides
AhaSlides ![]() यह सबसे अच्छा इंटरैक्टिव क्विज़ मेकर है जिसका उपयोग शिक्षा, प्रशिक्षण या मनोरंजन के उद्देश्यों के लिए किया जा सकता है। AhaSlides तुरंत मुक्त हो जाओ
यह सबसे अच्छा इंटरैक्टिव क्विज़ मेकर है जिसका उपयोग शिक्षा, प्रशिक्षण या मनोरंजन के उद्देश्यों के लिए किया जा सकता है। AhaSlides तुरंत मुक्त हो जाओ ![]() अनुकूलन योग्य टेम्पलेट
अनुकूलन योग्य टेम्पलेट![]() और उन्नत सुविधाएँ!
और उन्नत सुविधाएँ!
 अक्सर पूछे जाने वाले प्रश्न
अक्सर पूछे जाने वाले प्रश्न
![]() एक वृत्त का 2πr क्या है?
एक वृत्त का 2πr क्या है?
![]() 2πr एक वृत्त की परिधि का सूत्र है। इस सूत्र में:
2πr एक वृत्त की परिधि का सूत्र है। इस सूत्र में:
 "2" दर्शाता है कि आप त्रिज्या की दुगुनी लंबाई ले रहे हैं। परिधि वृत्त के चारों ओर की दूरी है, इसलिए आपको वृत्त के चारों ओर एक बार और फिर से जाना होगा, यही कारण है कि हम 2 से गुणा करते हैं।
"2" दर्शाता है कि आप त्रिज्या की दुगुनी लंबाई ले रहे हैं। परिधि वृत्त के चारों ओर की दूरी है, इसलिए आपको वृत्त के चारों ओर एक बार और फिर से जाना होगा, यही कारण है कि हम 2 से गुणा करते हैं। "π" (पाई) एक गणितीय स्थिरांक है जो लगभग 3.14159 के बराबर है। इसका उपयोग इसलिए किया जाता है क्योंकि यह वृत्त की परिधि और व्यास के बीच के संबंध को दर्शाता है।
"π" (पाई) एक गणितीय स्थिरांक है जो लगभग 3.14159 के बराबर है। इसका उपयोग इसलिए किया जाता है क्योंकि यह वृत्त की परिधि और व्यास के बीच के संबंध को दर्शाता है। "r" वृत्त की त्रिज्या को दर्शाता है, जो वृत्त के केंद्र से उसकी परिधि पर स्थित किसी भी बिंदु की दूरी है।
"r" वृत्त की त्रिज्या को दर्शाता है, जो वृत्त के केंद्र से उसकी परिधि पर स्थित किसी भी बिंदु की दूरी है।
![]() परिधि 2πr क्यों है?
परिधि 2πr क्यों है?
![]() एक वृत्त की परिधि का सूत्र, C = 2πr, pi (π) की परिभाषा और एक वृत्त के ज्यामितीय गुणों से आता है। पाई (π) एक वृत्त की परिधि और उसके व्यास के अनुपात को दर्शाता है। जब आप त्रिज्या (r) को 2π से गुणा करते हैं, तो आप अनिवार्य रूप से वृत्त के चारों ओर की दूरी की गणना करते हैं, जो परिधि की परिभाषा है।
एक वृत्त की परिधि का सूत्र, C = 2πr, pi (π) की परिभाषा और एक वृत्त के ज्यामितीय गुणों से आता है। पाई (π) एक वृत्त की परिधि और उसके व्यास के अनुपात को दर्शाता है। जब आप त्रिज्या (r) को 2π से गुणा करते हैं, तो आप अनिवार्य रूप से वृत्त के चारों ओर की दूरी की गणना करते हैं, जो परिधि की परिभाषा है।
![]() क्या परिधि त्रिज्या का 3.14 गुना है?
क्या परिधि त्रिज्या का 3.14 गुना है?
![]() नहीं, परिधि त्रिज्या के ठीक 3.14 गुना नहीं है। परिधि और वृत्त की त्रिज्या के बीच का संबंध सूत्र C = 2πr द्वारा दिया जाता है। जबकि π (पाई) लगभग 3.14159 है, परिधि त्रिज्या के 2 गुना π गुना है। इसलिए, परिधि त्रिज्या के 3.14 गुना से अधिक है; यह त्रिज्या के 2 गुना π गुना है।
नहीं, परिधि त्रिज्या के ठीक 3.14 गुना नहीं है। परिधि और वृत्त की त्रिज्या के बीच का संबंध सूत्र C = 2πr द्वारा दिया जाता है। जबकि π (पाई) लगभग 3.14159 है, परिधि त्रिज्या के 2 गुना π गुना है। इसलिए, परिधि त्रिज्या के 3.14 गुना से अधिक है; यह त्रिज्या के 2 गुना π गुना है।
![]() रेफरी:
रेफरी: ![]() ओमनी कैक्यूलेटर |
ओमनी कैक्यूलेटर | ![]() प्रोप्रो
प्रोप्रो







