Bagaimana untuk mengira Lilitan bulatan dengan tepat?
Lilitan bulatan ialah pengetahuan matematik asas dan diperlukan yang diperkenalkan di sekolah rendah atau menengah. Menguasai lilitan bulatan adalah penting bagi pelajar yang merancang untuk mengikuti kursus matematik yang lebih lanjut di sekolah menengah dan kolej dan bersedia untuk peperiksaan piawai seperti SAT dan ACT.
Kuiz 10 Lilitan Bulatan dalam artikel ini direka untuk menguji pemahaman anda tentang mencari jejari, diameter dan lilitan bulatan.
Isi kandungan:
Lingkaran formula bulatan
Sebelum mengambil ujian, mari kita imbas semula beberapa maklumat penting!
Bagaimana untuk mencari lilitan bulatanApakah lilitan bulatan?
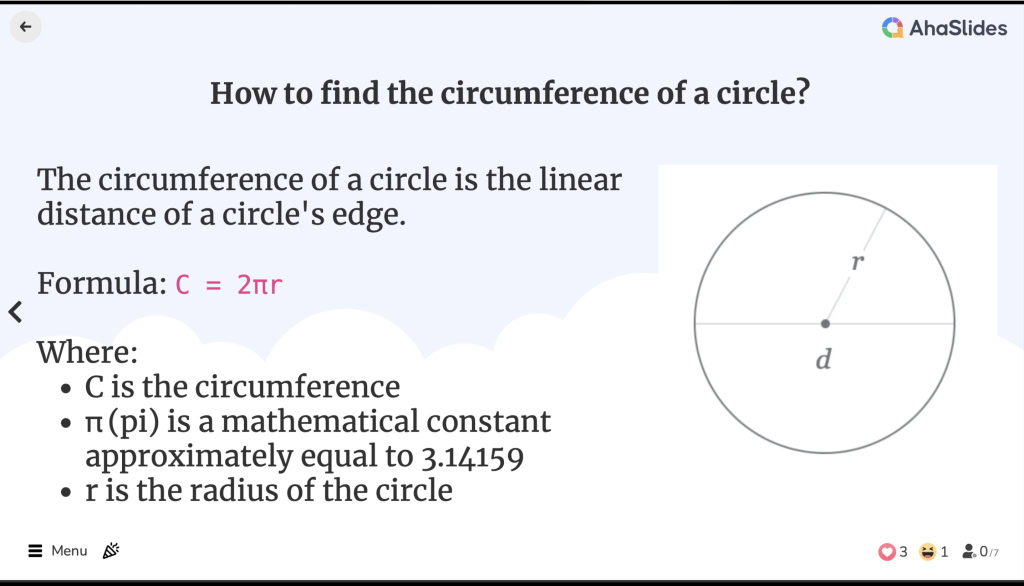
Lilitan bulatan ialah jarak linear tepi bulatan. Ia bersamaan dengan perimeter bentuk geometri, walaupun istilah perimeter hanya digunakan untuk poligon.
Bagaimana untuk mencari lilitan bulatan?
Lilitan formula bulatan ialah:
C = 2πr
di mana:
- C ialah lilitan
- π (pi) ialah pemalar matematik lebih kurang sama dengan 3.14159
- r ialah jejari bulatan itu
Jejari ialah jarak dari pusat bulatan ke mana-mana titik di tepi.
Diameter ialah dua kali jejari, jadi lilitan juga boleh dinyatakan sebagai:
C = πd
di mana:
- d ialah diameter
Sebagai contoh, jika jejari bulatan ialah 5 cm, maka lilitannya ialah:
C = 2πr = 2π * 5 cm = 10π cm
≈ 31.4 cm (dibundarkan kepada 2 tempat perpuluhan)
Lagi Petua daripada AhaSlides
- 70+ Soalan Kuiz Matematik Untuk Latihan Keseronokan dalam Kelas
- 10 Permainan Matematik Bilik Darjah Terbaik untuk Pelajar K12 yang Bosan
- 60 Idea Hebat Mengenai Asah Otak Untuk Dewasa | Kemas Kini 2023
AhaSlides ialah The Ultimate Quiz Maker
Buat permainan interaktif dalam sekelip mata dengan perpustakaan templat kami yang luas untuk menghilangkan kebosanan
Permainan dalam talian untuk dimainkan apabila bosanLilitan kuiz bulatan
Soalan 1: Jika lilitan kolam renang berbentuk bulat ialah 50 meter, berapakah jejarinya?
A. 7.95 meter
B. 8.00 meter
C. 15.91 meter
D. 25 meter
✅ Jawapan yang betul:
A. 7.95 meter
Keterangan:
Jejari boleh didapati dengan menyusun semula formula C = 2πr dan menyelesaikan untuk r: r = C / (2π). Memasukkan lilitan 50 meter yang diberikan dan menganggarkan π hingga 3.14, kami dapati jejari adalah lebih kurang 7.95 meter.
Soalan 2: Diameter bulatan ialah 14 inci. Berapakah jejarinya?
A. 28 inci
B.14 inci
C. 21 inci
D. 7 inci
✅ Jawapan yang betul:
D. 7 inci
Keterangan:
Oleh kerana diameter adalah dua kali panjang jejari (d = 2r), anda boleh mencari jejari dengan membahagikan diameter dengan 2 (r = d / 2). Dalam kes ini, membahagikan diameter yang diberi 14 inci dengan 2 menghasilkan a jejari 7 inci.
Cari lilitan bulatanSoalan 3: Antara pernyataan berikut, yang manakah benar tentang hubungan antara diameter dan lilitan bulatan?
A. Diameter ialah separuh lilitan.
B. Diameter adalah sama dengan lilitan.
C. Diameter ialah dua kali lilitan.
D. Diameter ialah π kali lilitan.
✅ Jawapan yang betul:
A. Diameter ialah separuh lilitan.
Keterangan:
Diameter adalah sama dengan 2 kali jejari, manakala lilitan adalah sama dengan 2π kali jejari. Oleh itu, diameter adalah separuh lilitan.
Soalan 4: Meja yang perlu kita duduki mempunyai lilitan 6.28 ela. Kita perlu mencari diameter meja.
A. 1 ela
B. 2 ela
C. 3 ela
D. 4 ela
✅ Jawapan yang betul:
B. 2 ela
Keterangan:
Lilitan bulatan dikira dengan mendarab diameter dengan pi (π). Dalam kes ini, lilitan diberikan sebagai 6.28 ela. Untuk mencari diameter, kita perlu membahagikan lilitan dengan pi. Membahagi 6.28 ela dengan pi memberi kita kira-kira 2 ela. Oleh itu, diameter meja ialah 2 ela.
Soalan 5: Sebuah taman bulat mempunyai lilitan 36 meter. Berapakah anggaran jejari taman itu?
A. 3.14 meter
B. 6 meter
C. 9 meter
D. 18 meter
✅ Jawapan yang betul:
C. 9 meter
Keterangan:
Untuk mencari jejari, gunakan formula untuk lilitan: C = 2πr. Susun semula formula untuk menyelesaikan jejari: r = C / (2π). Memasukkan lilitan 36 meter yang diberikan dan menggunakan nilai anggaran π sebagai 3.14, anda mendapat r = 36 / (2 * 3.14) ≈ 9 meter.
Soalan 6: Sebuah kolam renang berbentuk bulat mempunyai jejari 8 meter. Berapakah anggaran jarak yang dilalui oleh perenang mengelilingi kolam apabila melengkapkan satu pusingan?
A. 16 meter
B. 25 meter
C. 50 meter
D. 100 meter
✅ Jawapan yang betul:
C. 50 meter
Keterangan:
Untuk mencari jarak perenang mengelilingi kolam untuk satu pusingan, anda menggunakan formula lilitan (C = 2πr). Dalam kes ini, ia adalah 2 * 3.14 * 8 meter ≈ 50.24 meter, iaitu kira-kira 50 meter.
Soalan 7: Semasa mengukur gelung hula di dalam kelas, kumpulan C mendapati ia mempunyai jejari 7 inci. Berapakah lilitan gelung hula itu?
A. 39.6 inci
B. 37.6 inci
C. 47.6 inci
D. 49.6 inci
✅ Jawapan yang betul:
C. 47.6 inci
Keterangan:
Lilitan bulatan boleh didapati menggunakan formula C = 2πr, dengan r ialah jejari bulatan. Dalam kes ini, jejari gelung hula diberikan sebagai 7 inci. Memasukkan nilai ini ke dalam formula, kita mendapat C = 2π(7) = 14π inci. Dengan menganggarkan π hingga 3.14, kita boleh mengira lilitan sebagai 14(3.14) = 43.96 inci. Dibundarkan kepada persepuluh yang terdekat, lilitannya ialah 47.6 inci, yang sepadan dengan jawapan yang diberikan.
Soalan 8: Separuh bulatan mempunyai jejari 10 meter. Berapakah perimeternya?
A. 20 meter
B. 15 meter
C. 31.42 meter
D. 62.84 meter
✅ Jawapan yang betul:
C. 31.42 meter
Keterangan:Untuk mencari perimeter separuh bulatan, hitung separuh lilitan bulatan penuh dengan jejari 10 meter.
Lilitan contoh bulatanSoalan 9: Pasukan bola keranjang bermain dengan bola dengan jejari 5.6 inci. Berapakah lilitan setiap bola keranjang?
A. 11.2 inci
B. 17.6 inci
C. 22.4 inci
D. 35.2 inci
✅ Jawapan yang betul:
C. 22.4 inci
penjelasan:
Anda boleh menggunakan formula untuk lilitan bulatan, iaitu C = 2πr. Jejari yang diberi ialah 5.6 inci. Palamkan nilai ini ke dalam formula, kita mempunyai C = 2π * 5.6 inci. C ≈ 2 * 3.14 * 5.6 inci. C ≈ 11.2 * 5.6 inci. C ≈ 22.4 inci. Jadi, lilitan setiap bola keranjang adalah lebih kurang 22.4 inci. Ini mewakili jarak di sekeliling bola keranjang.
Soalan 10: Sarah dan dua rakannya sedang membina meja perkelahan bulat untuk perhimpunan mereka. Mereka tahu bahawa untuk mereka semua duduk dengan selesa di sekeliling meja, mereka memerlukan lilitan 18 kaki. Berapakah diameter yang mesti ada pada meja berkelah untuk mencapai lilitan yang betul?
A. 3 kaki
B. 6 kaki
C. 9 kaki
D. 12 kaki
✅ Jawapan yang betul:
B. 6 kaki
Keterangan:
Untuk mencari jejari, bahagikan lilitan dengan 2π, kita mempunyai r = C / (2π) r = 18 kaki / (2 * 3.14) r ≈ 18 kaki / 6.28 r ≈ 2.87 kaki (dibulatkan kepada perseratus terdekat).
Sekarang, untuk mencari diameter, hanya dua kali ganda jejari: Diameter = 2 * Diameter Jejari ≈ 2 * 2.87 kaki Diameter ≈ 5.74 kaki. Jadi, meja berkelah mestilah mempunyai diameter lebih kurang 5.74 kaki
Pengambilan kunci
AhaSlides ialah pembuat kuiz interaktif terbaik yang topi boleh digunakan untuk tujuan pendidikan, latihan atau hiburan. Semak keluar AhaSlides segera untuk mendapatkan percuma templat yang boleh disesuaikandan ciri lanjutan!
Soalan Lazim
Apakah 2πr bagi bulatan?
2πr ialah formula bagi lilitan bulatan. Dalam formula ini:
- "2" mewakili bahawa anda mengambil dua kali panjang jejari. Lilitan ialah jarak di sekeliling bulatan, jadi anda perlu mengelilingi bulatan sekali dan sekali lagi, itulah sebabnya kita darab dengan 2.
- "π" (pi) ialah pemalar matematik lebih kurang sama dengan 3.14159. Ia digunakan kerana ia mewakili hubungan antara lilitan dan diameter bulatan.
- "r" mewakili jejari bulatan, iaitu jarak dari pusat bulatan ke mana-mana titik pada lilitannya.
Mengapakah lilitan ialah 2πr?
Formula untuk lilitan bulatan, C = 2πr, berasal daripada takrifan pi (π) dan sifat geometri bulatan. Pi (π) mewakili nisbah lilitan bulatan kepada diameternya. Apabila anda mendarab jejari (r) dengan 2π, anda pada asasnya mengira jarak di sekeliling bulatan, yang merupakan takrifan lilitan.
Adakah lilitan 3.14 kali jejari?
Tidak, lilitan tidak betul-betul 3.14 kali jejari. Hubungan antara lilitan dan jejari bulatan diberikan oleh formula C = 2πr. Walaupun π (pi) adalah lebih kurang 3.14159, lilitan ialah 2 kali π kali jejari. Jadi, lilitan adalah lebih daripada sekadar 3.14 kali jejari; ia adalah 2 kali π kali jejari.
Ruj: Omni Caculator | Prof
Tags: Idea Kuiz
