จะคำนวณเส้นรอบวงของวงกลมได้อย่างไร?
เส้นรอบวงของวงกลมเป็นความรู้พื้นฐานทางคณิตศาสตร์ที่จำเป็นซึ่งนำมาใช้ในโรงเรียนประถมศึกษาหรือมัธยมศึกษาตอนต้น การเรียนรู้เส้นรอบวงของวงกลมเป็นสิ่งสำคัญสำหรับนักเรียนที่วางแผนจะเรียนหลักสูตรคณิตศาสตร์ขั้นสูงในโรงเรียนมัธยมและวิทยาลัย และเตรียมความพร้อมสำหรับการสอบมาตรฐาน เช่น SAT และ ACT
แบบทดสอบเส้นรอบวง 10 เส้นในบทความนี้ออกแบบมาเพื่อทดสอบความเข้าใจของคุณในการค้นหารัศมี เส้นผ่านศูนย์กลาง และเส้นรอบวงของวงกลม
สารบัญ:
เส้นรอบวงสูตรวงกลม
ก่อนทำแบบทดสอบ เรามาสรุปข้อมูลสำคัญกันก่อน!
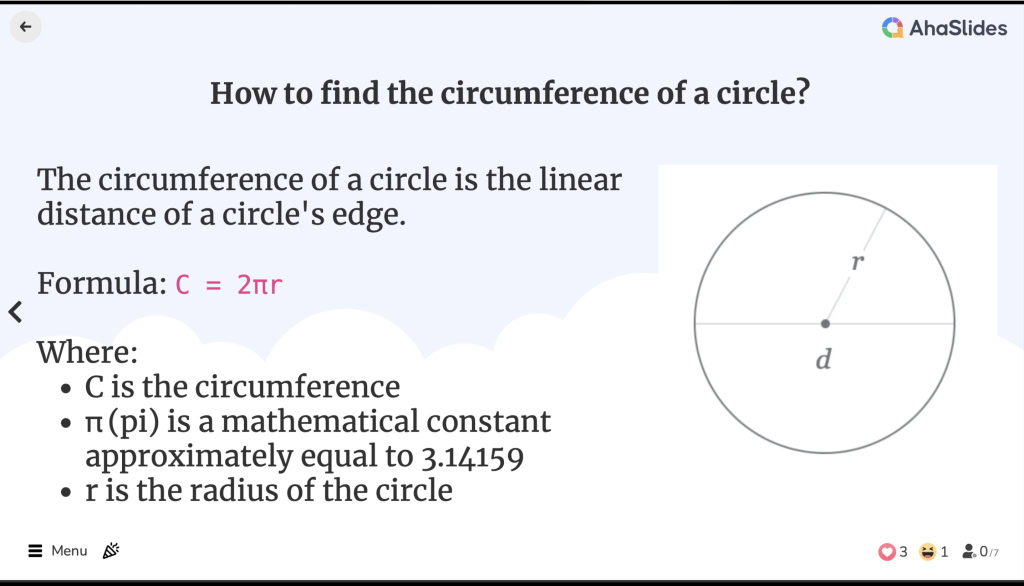
วิธีหาเส้นรอบวงของวงกลมเส้นรอบวงของวงกลมคืออะไร?
เส้นรอบวงของวงกลมคือระยะทางเชิงเส้นของขอบของวงกลม ซึ่งเทียบเท่ากับเส้นรอบวงของรูปทรงเรขาคณิต แม้ว่าคำว่าเส้นรอบวงจะใช้กับรูปหลายเหลี่ยมเท่านั้น
จะหาเส้นรอบวงของวงกลมได้อย่างไร?
เส้นรอบวงของสูตรวงกลมคือ:
C = 2πr
ที่:
- C คือเส้นรอบวง
- π (pi) เป็นค่าคงที่ทางคณิตศาสตร์ประมาณเท่ากับ 3.14159
- r คือรัศมีของวงกลม
รัศมีคือระยะห่างจากศูนย์กลางของวงกลมถึงจุดใดๆ บนขอบ
เส้นผ่านศูนย์กลางเป็นสองเท่าของรัศมี ดังนั้นเส้นรอบวงจึงสามารถแสดงเป็น:
C = πd
ที่:
- d คือเส้นผ่านศูนย์กลาง
ตัวอย่างเช่น ถ้ารัศมีของวงกลมคือ 5 ซม. เส้นรอบวงจะเป็นดังนี้:
C = 2πr = 2π * 5 cm = 10π cm
มีความยาว 31.4 ซม. (ปัดเศษทศนิยม 2 ตำแหน่ง)
เคล็ดลับเพิ่มเติมจาก AhaSlides
- 70+ คำถามแบบทดสอบคณิตศาสตร์สำหรับแบบฝึกหัดแสนสนุกในชั้นเรียน
- 10 เกมคณิตศาสตร์ในห้องเรียนที่ดีที่สุดสำหรับนักเรียน K12 ที่เบื่อ
- 60 ไอเดียสุดเจ๋งเกี่ยวกับของเล่นพัฒนาสมองสำหรับผู้ใหญ่ | อัปเดตปี 2023
AhaSlides เป็นโปรแกรมสร้างแบบทดสอบขั้นสูงสุด
สร้างเกมแบบโต้ตอบได้ในทันทีด้วยคลังเทมเพลตที่กว้างขวางของเราเพื่อขจัดความเบื่อหน่าย
เกมออนไลน์ที่เล่นเมื่อเบื่อแบบทดสอบเรื่องเส้นรอบวงของวงกลม
คำถามที่ 1: ถ้าเส้นรอบวงของสระว่ายน้ำทรงกลมคือ 50 เมตร รัศมีของมันจะเป็นเท่าใด
ก. 7.95 เมตร
บ. 8.00 ม
ค. 15.91 ม
ง. 25 เมตร
✅ คำตอบที่ถูกต้อง:
ก. 7.95 เมตร
คำอธิบาย:
รัศมีหาได้โดยการจัดเรียงสูตร C = 2πr ใหม่ แล้วแก้หา r: r = C / (2π) เมื่อแทนเส้นรอบวงที่กำหนด 50 เมตรและประมาณ π ถึง 3.14 เราจะพบว่ารัศมีจะอยู่ที่ประมาณ 7.95 เมตร
คำถามที่ 2: เส้นผ่านศูนย์กลางของวงกลมคือ 14 นิ้ว รัศมีของมันคืออะไร?
ก.28นิ้ว
บ.14นิ้ว
ค.21นิ้ว
ส.7นิ้ว
✅ คำตอบที่ถูกต้อง:
ส.7นิ้ว
คำอธิบาย:
เนื่องจากเส้นผ่านศูนย์กลางเป็นสองเท่าของความยาวของรัศมี (d = 2r) คุณจึงสามารถหารัศมีได้โดยการหารเส้นผ่านศูนย์กลางด้วย 2 (r = d / 2) ในกรณีนี้ การหารเส้นผ่านศูนย์กลางที่กำหนด 14 นิ้วด้วย 2 จะได้ค่า a รัศมี 7 นิ้ว.
หาเส้นรอบวงของวงกลมคำถามที่ 3: ข้อความใดต่อไปนี้เป็นจริงเกี่ยวกับความสัมพันธ์ระหว่างเส้นผ่านศูนย์กลางกับเส้นรอบวงของวงกลม
ก. เส้นผ่านศูนย์กลางคือครึ่งหนึ่งของเส้นรอบวง
B. เส้นผ่านศูนย์กลางเท่ากับเส้นรอบวง
C. เส้นผ่านศูนย์กลางเป็นสองเท่าของเส้นรอบวง
ง. เส้นผ่านศูนย์กลางคือ π คูณเส้นรอบวง
✅ คำตอบที่ถูกต้อง:
ก. เส้นผ่านศูนย์กลางคือครึ่งหนึ่งของเส้นรอบวง
คำอธิบาย:
เส้นผ่านศูนย์กลางเท่ากับ 2 เท่าของรัศมี ในขณะที่เส้นรอบวงเท่ากับ 2π คูณรัศมี ดังนั้นเส้นผ่านศูนย์กลางจึงเป็นครึ่งหนึ่งของเส้นรอบวง
คำถามที่ 4 โต๊ะที่เรานั่งมีเส้นรอบวง 6.28 หลา เราต้องหาเส้นผ่านศูนย์กลางของโต๊ะ
ก. 1 หลา
บี 2 หลา
ค. 3 หลา
ง. 4 หลา
✅ คำตอบที่ถูกต้อง:
บี 2 หลา
คำอธิบาย:
เส้นรอบวงของวงกลมคำนวณโดยการคูณเส้นผ่านศูนย์กลางด้วย pi (π) ในกรณีนี้ เส้นรอบวงจะเท่ากับ 6.28 หลา หากต้องการหาเส้นผ่านศูนย์กลาง เราต้องหารเส้นรอบวงด้วยพาย การหาร 6.28 หลาด้วยพาย จะได้ประมาณ 2 หลา ดังนั้น เส้นผ่านศูนย์กลางของโต๊ะคือ 2 หลา
คำถามที่ 5: สวนทรงกลมมีเส้นรอบวง 36 เมตร รัศมีของสวนประมาณเท่าไร?
ก. 3.14 เมตร
บ. 6 ม
ค. 9 ม
ง. 18 เมตร
✅ คำตอบที่ถูกต้อง:
ค. 9 ม
คำอธิบาย:
หากต้องการหารัศมี ให้ใช้สูตรเส้นรอบวง: C = 2πr จัดเรียงสูตรใหม่เพื่อแก้รัศมี: r = C / (2π) เมื่อแทนค่าเส้นรอบวงที่กำหนด 36 เมตร และใช้ค่าประมาณ π เป็น 3.14 คุณจะได้ r = 36 / (2 * 3.14) กลับไปยัง 9 เมตร
คำถามที่ 6: สระว่ายน้ำทรงกลมมีรัศมี 8 เมตร ระยะทางโดยประมาณที่นักว่ายน้ำเคลื่อนที่ไปรอบๆ สระเมื่อเสร็จสิ้นหนึ่งรอบคือเท่าใด
ก. 16 เมตร
บ. 25 ม
ค. 50 ม
ง. 100 เมตร
✅ คำตอบที่ถูกต้อง:
ค. 50 ม
คำอธิบาย:
หากต้องการค้นหาระยะทางที่นักว่ายน้ำเดินทางรอบสระเป็นเวลา 2 รอบ ให้ใช้สูตรเส้นรอบวง (C = 2πr) ในกรณีนี้คือ 3.14 * 8 * 50.24 เมตร กลับไปยัง 50 เมตร ซึ่งก็คือประมาณ XNUMX เมตร
คำถามที่ 7: เมื่อวัดฮูลาฮูปในชั้นเรียน กลุ่ม C พบว่ามีรัศมี 7 นิ้ว ฮูลาฮูปมีเส้นรอบวงเท่าไร?
ก.39.6นิ้ว
บ.37.6นิ้ว
ค.47.6นิ้ว
ส.49.6นิ้ว
✅ คำตอบที่ถูกต้อง:
ค.47.6นิ้ว
คำอธิบาย:
เส้นรอบวงของวงกลมหาได้จากสูตร C = 2πr โดยที่ r คือรัศมีของวงกลม ในกรณีนี้ รัศมีของฮูลาฮูปคือ 7 นิ้ว เมื่อแทนค่านี้ลงในสูตร เราจะได้ C = 2π(7) = 14π นิ้ว เมื่อประมาณ π ถึง 3.14 เราสามารถคำนวณเส้นรอบวงได้เป็น 14 (3.14) = 43.96 นิ้ว เมื่อปัดเศษให้เป็นทศนิยมที่ใกล้ที่สุด เส้นรอบวงคือ 47.6 นิ้ว ซึ่งตรงกับคำตอบที่ให้ไว้
คำถามที่ 8 ครึ่งวงกลมมีรัศมี 10 เมตร เส้นรอบวงของมันคืออะไร?
ก. 20 เมตร
บ. 15 ม
ค. 31.42 ม
ง. 62.84 เมตร
✅ คำตอบที่ถูกต้อง:
ค. 31.42 ม
คำอธิบาย:ในการหาเส้นรอบวงของครึ่งวงกลม ให้คำนวณครึ่งหนึ่งของเส้นรอบวงของวงกลมเต็มวงกลมโดยมีรัศมี 10 เมตร
ตัวอย่างเส้นรอบวงของวงกลมคำถามที่ 9: ทีมบาสเก็ตบอลเล่นโดยใช้ลูกบอลที่มีรัศมี 5.6 นิ้ว ลูกบาสแต่ละลูกมีขนาดเส้นรอบวงเท่าไร?
ก.11.2นิ้ว
บ.17.6นิ้ว
ค.22.4นิ้ว
ส.35.2นิ้ว
✅ คำตอบที่ถูกต้อง:
ค.22.4นิ้ว
คำอธิบาย:
คุณสามารถใช้สูตรหาเส้นรอบวงของวงกลมได้ ซึ่งก็คือ C = 2πr รัศมีที่กำหนดคือ 5.6 นิ้ว แทนค่านี้ลงในสูตรจะได้ C = 2π * 5.6 นิ้ว ค 2 * 3.14 * 5.6 นิ้ว ค µ 11.2 * 5.6 นิ้ว. ค µ 22.4 นิ้ว. ดังนั้น เส้นรอบวงของลูกบาสเก็ตบอลแต่ละลูกจะอยู่ที่ประมาณ 22.4 นิ้ว นี่แสดงถึงระยะทางรอบบาสเก็ตบอล
คำถาม 10: ซาราห์และเพื่อนสองคนของเธอกำลังสร้างโต๊ะปิกนิกทรงกลมสำหรับการประชุมของพวกเขา พวกเขารู้ว่าเพื่อให้ทุกคนนั่งรอบโต๊ะได้อย่างสบาย พวกเขาจำเป็นต้องมีเส้นรอบวง 18 ฟุต โต๊ะปิกนิกต้องมีเส้นผ่านศูนย์กลางเท่าใดเพื่อให้ได้เส้นรอบวงที่ถูกต้อง?
ก. 3 ฟุต
บี 6 ฟุต
ค. 9 ฟุต
ง. 12 ฟุต
✅ คำตอบที่ถูกต้อง:
บี 6 ฟุต
คำอธิบาย:
หากต้องการหารัศมี ให้หารเส้นรอบวงด้วย 2π เราจะได้ r = C / (2π) r = 18 ฟุต / (2 * 3.14) r พรีเมี่ยม 18 ฟุต / 6.28 r พรีเมี่ยม 2.87 ฟุต (ปัดเศษเป็นทศนิยมที่ใกล้ที่สุด)
ตอนนี้ หากต้องการหาเส้นผ่านศูนย์กลาง เพียงเพิ่มรัศมีเป็นสองเท่า: เส้นผ่านศูนย์กลาง = 2 * เส้นผ่านศูนย์กลางรัศมี µ 2 * 2.87 ฟุต เส้นผ่านศูนย์กลาง กลับไปยัง 5.74 ฟุต ดังนั้นโต๊ะปิคนิคจะต้องมีเส้นผ่านศูนย์กลางประมาณ 5.74 ฟุต
ประเด็นที่สำคัญ
AhaSlides เป็นเครื่องมือสร้างแบบทดสอบแบบโต้ตอบที่ดีที่สุดที่สามารถใช้เพื่อการศึกษา การฝึกอบรม หรือเพื่อความบันเทิง ลองดู AhaSlides ทันทีเพื่อรับฟรี เทมเพลตที่ปรับแต่งได้และคุณสมบัติขั้นสูง!
คำถามที่พบบ่อย
2πr ของวงกลมคืออะไร?
2πr เป็นสูตรสำหรับเส้นรอบวงของวงกลม ในสูตรนี้:
- "2" แสดงว่าคุณกำลังใช้ความยาวของรัศมีเป็นสองเท่า เส้นรอบวงคือระยะทางรอบวงกลม ดังนั้นคุณต้องวนรอบวงกลมครั้งแล้วครั้งเล่า ซึ่งเป็นสาเหตุที่เราคูณด้วย 2
- "π" (pi) เป็นค่าคงที่ทางคณิตศาสตร์ประมาณเท่ากับ 3.14159 ใช้เพราะมันแสดงถึงความสัมพันธ์ระหว่างเส้นรอบวงและเส้นผ่านศูนย์กลางของวงกลม
- "r" หมายถึงรัศมีของวงกลม ซึ่งเป็นระยะทางจากศูนย์กลางของวงกลมถึงจุดใดๆ บนเส้นรอบวง
ทำไมเส้นรอบวงถึงเป็น 2πr?
สูตรสำหรับเส้นรอบวงของวงกลม C = 2πr มาจากคำจำกัดความของพาย (π) และคุณสมบัติทางเรขาคณิตของวงกลม Pi (π) แสดงถึงอัตราส่วนของเส้นรอบวงของวงกลมต่อเส้นผ่านศูนย์กลาง เมื่อคุณคูณรัศมี (r) ด้วย 2π คุณจะคำนวณระยะทางรอบวงกลม ซึ่งเป็นคำจำกัดความของเส้นรอบวง
เส้นรอบวงเป็น 3.14 เท่าของรัศมีหรือไม่?
ไม่ใช่ เส้นรอบวงไม่เท่ากับ 3.14 เท่าของรัศมีพอดี ความสัมพันธ์ระหว่างเส้นรอบวงกับรัศมีของวงกลมหาได้จากสูตร C = 2πr ขณะที่ π (พาย) มีค่าประมาณ 3.14159 แต่เส้นรอบวงจะเป็น 2 คูณ π คูณรัศมี ดังนั้น เส้นรอบวงจึงมากกว่ารัศมีเพียง 3.14 เท่า มันคือ 2 คูณ π คูณรัศมี
Ref: เครื่องคิดเลขออมนิ | โปรพรอฟ
คีย์เวิร์ด: แบบทดสอบไอเดีย
