![]() Jak přesně vypočítat obvod kruhu?
Jak přesně vypočítat obvod kruhu?
![]() Obvod kruhu je základní a povinná matematická znalost zavedená na základní nebo střední škole. Zvládnutí obvodu kruhu je nezbytné pro studenty, kteří plánují absolvovat pokročilejší kurzy matematiky na střední a vysoké škole a připravit se na standardizované zkoušky, jako je SAT a ACT.
Obvod kruhu je základní a povinná matematická znalost zavedená na základní nebo střední škole. Zvládnutí obvodu kruhu je nezbytné pro studenty, kteří plánují absolvovat pokročilejší kurzy matematiky na střední a vysoké škole a připravit se na standardizované zkoušky, jako je SAT a ACT.
![]() Kvíz 10 obvodů kruhu v tomto článku je navržen tak, aby otestoval vaše chápání hledání poloměru, průměru a obvodu kruhu.
Kvíz 10 obvodů kruhu v tomto článku je navržen tak, aby otestoval vaše chápání hledání poloměru, průměru a obvodu kruhu.
![]() Obsah:
Obsah:
 Obvod kruhového vzorce
Obvod kruhového vzorce
![]() Než se pustíte do testu, zrekapitulujme si pár zásadních informací!
Než se pustíte do testu, zrekapitulujme si pár zásadních informací!
 Jak zjistit obvod kruhu
Jak zjistit obvod kruhu![]() Jaký je obvod kruhu?
Jaký je obvod kruhu?
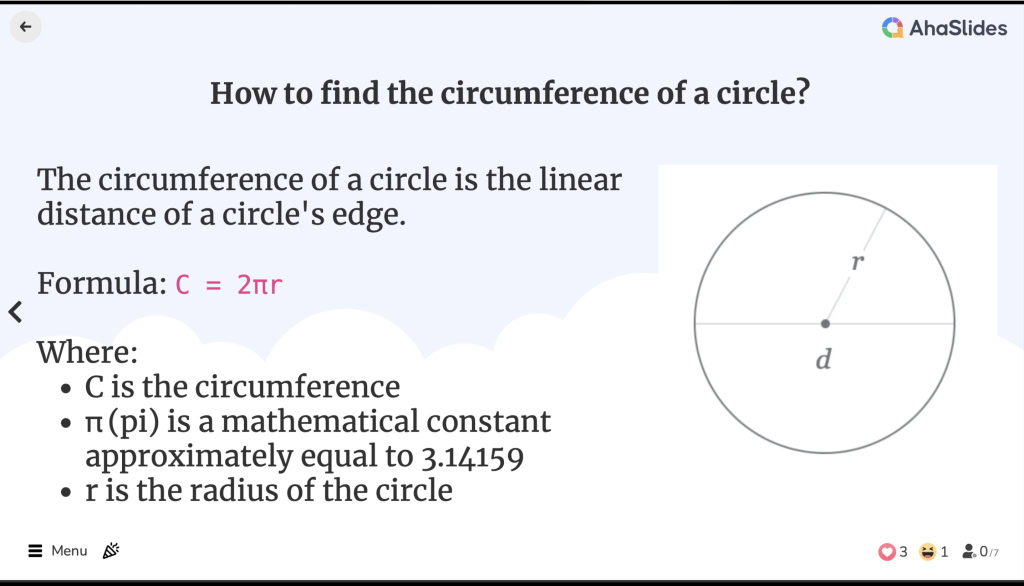
![]() Obvod kruhu je lineární vzdálenost okraje kruhu. Je ekvivalentní k obvodu geometrického tvaru, ačkoli termín obvod se používá pouze pro mnohoúhelníky.
Obvod kruhu je lineární vzdálenost okraje kruhu. Je ekvivalentní k obvodu geometrického tvaru, ačkoli termín obvod se používá pouze pro mnohoúhelníky.
![]() Jak zjistit obvod kruhu?
Jak zjistit obvod kruhu?
![]() Obvod kruhového vzorce je:
Obvod kruhového vzorce je:
C = 2πr
![]() kde:
kde:
 C je obvod
C je obvod π (pi) je matematická konstanta přibližně rovna 3.14159
π (pi) je matematická konstanta přibližně rovna 3.14159 r je poloměr kružnice
r je poloměr kružnice
![]() Poloměr je vzdálenost od středu kruhu k libovolnému bodu na okraji.
Poloměr je vzdálenost od středu kruhu k libovolnému bodu na okraji.
![]() Průměr je dvojnásobkem poloměru, takže obvod lze také vyjádřit jako:
Průměr je dvojnásobkem poloměru, takže obvod lze také vyjádřit jako:
C = πd
![]() kde:
kde:
 d je průměr
d je průměr
![]() Pokud je například poloměr kruhu 5 cm, pak je obvod:
Pokud je například poloměr kruhu 5 cm, pak je obvod:
C = 2πr = 2π * 5 cm = 10π cm
![]() ≈ 31.4 cm (zaokrouhleno na 2 desetinná místa)
≈ 31.4 cm (zaokrouhleno na 2 desetinná místa)
 Další tipy od AhaSlides
Další tipy od AhaSlides
 70+ matematických kvízových otázek pro zábavná cvičení ve třídě
70+ matematických kvízových otázek pro zábavná cvičení ve třídě 10 nejlepších matematických her ve třídě pro nudné studenty K12
10 nejlepších matematických her ve třídě pro nudné studenty K12 60 úžasných nápadů na hlavolamy pro dospělé | Aktualizace 2023
60 úžasných nápadů na hlavolamy pro dospělé | Aktualizace 2023
![]() AhaSlides je The Ultimate Quiz Maker
AhaSlides je The Ultimate Quiz Maker
![]() Vytvářejte interaktivní hry během okamžiku s naší rozsáhlou knihovnou šablon, abyste zabili nudu
Vytvářejte interaktivní hry během okamžiku s naší rozsáhlou knihovnou šablon, abyste zabili nudu

 Online hry, které můžete hrát, když se nudíte
Online hry, které můžete hrát, když se nudíte Kvíz o obvodu kruhu
Kvíz o obvodu kruhu
![]() Otázka 1: Pokud je obvod kruhového bazénu 50 metrů, jaký je jeho poloměr?
Otázka 1: Pokud je obvod kruhového bazénu 50 metrů, jaký je jeho poloměr?
![]() A. 7.95 metru
A. 7.95 metru
![]() B. 8.00 metru
B. 8.00 metru
![]() C. 15.91 metrů
C. 15.91 metrů
![]() D. 25 metrů
D. 25 metrů
(Tj. ![]() Správná odpověď:
Správná odpověď:
![]() A. 7.95 metru
A. 7.95 metru
![]() Vysvětlení:
Vysvětlení:
![]() Poloměr lze nalézt přeskupením vzorce C = 2πr a řešením pro r: r = C / (2π). Zapojením daného obvodu 50 metrů a přiblížením π na 3.14 zjistíme, že poloměr je přibližně 7.95 metru.
Poloměr lze nalézt přeskupením vzorce C = 2πr a řešením pro r: r = C / (2π). Zapojením daného obvodu 50 metrů a přiblížením π na 3.14 zjistíme, že poloměr je přibližně 7.95 metru.
![]() Otázka 2: Průměr kruhu je 14 palců. Jaký je její poloměr?
Otázka 2: Průměr kruhu je 14 palců. Jaký je její poloměr?
![]() A. 28 palců
A. 28 palců
![]() B.14 palců
B.14 palců
![]() C. 21 palců
C. 21 palců
![]() D. 7 palců
D. 7 palců
(Tj. ![]() Správná odpověď:
Správná odpověď:
![]() D. 7 palců
D. 7 palců
![]() Vysvětlení:
Vysvětlení:
![]() Protože průměr je dvojnásobkem délky poloměru (d = 2r), můžete poloměr zjistit vydělením průměru 2 (r = d / 2). V tomto případě vydělení daného průměru 14 palců 2 získá a poloměr 7 palců.
Protože průměr je dvojnásobkem délky poloměru (d = 2r), můžete poloměr zjistit vydělením průměru 2 (r = d / 2). V tomto případě vydělení daného průměru 14 palců 2 získá a poloměr 7 palců.

 Najděte obvod kruhu
Najděte obvod kruhu![]() Otázka 3: Které z následujících tvrzení o vztahu mezi průměrem a obvodem kruhu je pravdivé?
Otázka 3: Které z následujících tvrzení o vztahu mezi průměrem a obvodem kruhu je pravdivé?
![]() A. Průměr je polovina obvodu.
A. Průměr je polovina obvodu.
![]() B. Průměr je stejný jako obvod.
B. Průměr je stejný jako obvod.
![]() C. Průměr je dvojnásobek obvodu.
C. Průměr je dvojnásobek obvodu.
![]() D. Průměr je π krát obvod.
D. Průměr je π krát obvod.
(Tj. ![]() Správná odpověď:
Správná odpověď:
![]() A. Průměr je polovina obvodu.
A. Průměr je polovina obvodu.
![]() Vysvětlení:
Vysvětlení:
![]() Průměr je roven 2násobku poloměru, zatímco obvod je roven 2πnásobku poloměru. Proto je průměr poloviční než obvod.
Průměr je roven 2násobku poloměru, zatímco obvod je roven 2πnásobku poloměru. Proto je průměr poloviční než obvod.
![]() Otázka 4: Stůl, u kterého musíme sedět, má obvod 6.28 yardů. Musíme najít průměr stolu.
Otázka 4: Stůl, u kterého musíme sedět, má obvod 6.28 yardů. Musíme najít průměr stolu.
![]() A. 1 yard
A. 1 yard
![]() B. 2 yardy
B. 2 yardy
![]() C. 3 yardy
C. 3 yardy
![]() D. 4 yardy
D. 4 yardy
(Tj. ![]() Správná odpověď:
Správná odpověď:
![]() B. 2 yardy
B. 2 yardy
![]() Vysvětlení:
Vysvětlení:
![]() Obvod kruhu se vypočítá vynásobením průměru pí (π). V tomto případě je obvod udán jako 6.28 yardů. Abychom zjistili průměr, musíme vydělit obvod pí. Vydělením 6.28 yardů pí získáme přibližně 2 yardy. Proto je průměr stolu 2 yardy.
Obvod kruhu se vypočítá vynásobením průměru pí (π). V tomto případě je obvod udán jako 6.28 yardů. Abychom zjistili průměr, musíme vydělit obvod pí. Vydělením 6.28 yardů pí získáme přibližně 2 yardy. Proto je průměr stolu 2 yardy.
![]() Otázka 5: Kruhová zahrada má obvod 36 metrů. Jaký je přibližný poloměr zahrady?
Otázka 5: Kruhová zahrada má obvod 36 metrů. Jaký je přibližný poloměr zahrady?
![]() A. 3.14 metru
A. 3.14 metru
![]() B. 6 metru
B. 6 metru
![]() C. 9 metrů
C. 9 metrů
![]() D. 18 metrů
D. 18 metrů
(Tj. ![]() Správná odpověď:
Správná odpověď:
![]() C. 9 metrů
C. 9 metrů
![]() Vysvětlení:
Vysvětlení:
![]() Chcete-li zjistit poloměr, použijte vzorec pro obvod: C = 2πr. Uspořádejte vzorec pro řešení pro poloměr: r = C / (2π). Zapojením daného obvodu 36 metrů a použitím přibližné hodnoty π jako 3.14 dostanete r = 36 / (2 * 3.14) ≈ 9 metrů.
Chcete-li zjistit poloměr, použijte vzorec pro obvod: C = 2πr. Uspořádejte vzorec pro řešení pro poloměr: r = C / (2π). Zapojením daného obvodu 36 metrů a použitím přibližné hodnoty π jako 3.14 dostanete r = 36 / (2 * 3.14) ≈ 9 metrů.
![]() Otázka 6: Kruhový bazén má poloměr 8 metrů. Jaká je přibližná vzdálenost, kterou plavec urazí kolem bazénu, když dokončí jedno kolo?
Otázka 6: Kruhový bazén má poloměr 8 metrů. Jaká je přibližná vzdálenost, kterou plavec urazí kolem bazénu, když dokončí jedno kolo?
![]() A. 16 metru
A. 16 metru
![]() B. 25 metru
B. 25 metru
![]() C. 50 metrů
C. 50 metrů
![]() D. 100 metrů
D. 100 metrů
(Tj. ![]() Správná odpověď:
Správná odpověď:
![]() C. 50 metrů
C. 50 metrů
![]() Vysvětlení:
Vysvětlení:
![]() Chcete-li zjistit vzdálenost, kterou plavec urazí kolem bazénu za jedno kolo, použijte vzorec pro obvod (C = 2πr). V tomto případě je to 2 * 3.14 * 8 metrů ≈ 50.24 metrů, což je přibližně 50 metrů.
Chcete-li zjistit vzdálenost, kterou plavec urazí kolem bazénu za jedno kolo, použijte vzorec pro obvod (C = 2πr). V tomto případě je to 2 * 3.14 * 8 metrů ≈ 50.24 metrů, což je přibližně 50 metrů.
![]() Otázka 7: Při měření hula hoop ve třídě skupina C zjistila, že má poloměr 7 palců. Jaký je obvod hula hoopu?
Otázka 7: Při měření hula hoop ve třídě skupina C zjistila, že má poloměr 7 palců. Jaký je obvod hula hoopu?
![]() A. 39.6 palců
A. 39.6 palců
![]() B. 37.6 palce
B. 37.6 palce
![]() C. 47.6 palců
C. 47.6 palců
![]() D. 49.6 palců
D. 49.6 palců
(Tj. ![]() Správná odpověď:
Správná odpověď:
![]() C. 47.6 palců
C. 47.6 palců
![]() Vysvětlení:
Vysvětlení:
![]() Obvod kruhu lze zjistit pomocí vzorce C = 2πr, kde r je poloměr kruhu. V tomto případě je poloměr hula hoopu udán jako 7 palců. Zapojením této hodnoty do vzorce dostaneme C = 2π(7) = 14π palců. Při přiblížení π k 3.14 můžeme vypočítat obvod jako 14(3.14) = 43.96 palce. Zaokrouhleno na desetinu je obvod 47.6 palce, což odpovídá dané odpovědi.
Obvod kruhu lze zjistit pomocí vzorce C = 2πr, kde r je poloměr kruhu. V tomto případě je poloměr hula hoopu udán jako 7 palců. Zapojením této hodnoty do vzorce dostaneme C = 2π(7) = 14π palců. Při přiblížení π k 3.14 můžeme vypočítat obvod jako 14(3.14) = 43.96 palce. Zaokrouhleno na desetinu je obvod 47.6 palce, což odpovídá dané odpovědi.
![]() Otázka 8: Půlkruh má poloměr 10 metrů. Jaký je jeho obvod?
Otázka 8: Půlkruh má poloměr 10 metrů. Jaký je jeho obvod?
![]() A. 20 metru
A. 20 metru
![]() B. 15 metru
B. 15 metru
![]() C. 31.42 metrů
C. 31.42 metrů
![]() D. 62.84 metrů
D. 62.84 metrů
(Tj. ![]() Správná odpověď:
Správná odpověď:
![]() C. 31.42 metrů
C. 31.42 metrů
![]() Vysvětlení:
Vysvětlení:![]() Chcete-li zjistit obvod půlkruhu, vypočítejte polovinu obvodu plného kruhu o poloměru 10 metrů.
Chcete-li zjistit obvod půlkruhu, vypočítejte polovinu obvodu plného kruhu o poloměru 10 metrů.

 Příklad obvodu kruhu
Příklad obvodu kruhu![]() Otázka 9: Basketbalový tým hraje s míčem o poloměru 5.6 palce. Jaký je obvod každého basketbalového míče?
Otázka 9: Basketbalový tým hraje s míčem o poloměru 5.6 palce. Jaký je obvod každého basketbalového míče?
![]() A. 11.2 palců
A. 11.2 palců
![]() B. 17.6 palce
B. 17.6 palce
![]() C. 22.4 palců
C. 22.4 palců
![]() D. 35.2 palců
D. 35.2 palců
(Tj. ![]() Správná odpověď:
Správná odpověď:
![]() C. 22.4 palců
C. 22.4 palců
![]() Vysvětlení:
Vysvětlení:
![]() Můžete použít vzorec pro obvod kruhu, který je C = 2πr. Udávaný rádius je 5.6 palce. Vložte tuto hodnotu do vzorce, máme C = 2π * 5.6 palce. C ≈ 2 * 3.14 * 5.6 palce. C ≈ 11.2 * 5.6 palce. C ≈ 22.4 palce. Obvod každého basketbalového míče je tedy přibližně 22.4 palce. To představuje vzdálenost kolem basketbalového míče.
Můžete použít vzorec pro obvod kruhu, který je C = 2πr. Udávaný rádius je 5.6 palce. Vložte tuto hodnotu do vzorce, máme C = 2π * 5.6 palce. C ≈ 2 * 3.14 * 5.6 palce. C ≈ 11.2 * 5.6 palce. C ≈ 22.4 palce. Obvod každého basketbalového míče je tedy přibližně 22.4 palce. To představuje vzdálenost kolem basketbalového míče.
![]() Otázka 10: Sarah a její dva přátelé stavěli kruhový piknikový stůl pro své setkání. Věděli, že k tomu, aby se všichni pohodlně usadili kolem stolu, potřebují obvod 18 stop. Jaký průměr musí mít piknikový stůl, aby dosáhl správného obvodu?
Otázka 10: Sarah a její dva přátelé stavěli kruhový piknikový stůl pro své setkání. Věděli, že k tomu, aby se všichni pohodlně usadili kolem stolu, potřebují obvod 18 stop. Jaký průměr musí mít piknikový stůl, aby dosáhl správného obvodu?
![]() A. 3 stopy
A. 3 stopy
![]() B. 6 stop
B. 6 stop
![]() C. 9 stop
C. 9 stop
![]() D. 12 stop
D. 12 stop
(Tj. ![]() Správná odpověď:
Správná odpověď:
![]() B. 6 stop
B. 6 stop
![]() Vysvětlení:
Vysvětlení:
![]() Chcete-li zjistit poloměr, vydělte obvod 2π, máme r = C / (2π) r = 18 stop / (2 * 3.14) r ≈ 18 stop / 6.28 r ≈ 2.87 stop (zaokrouhleno na nejbližší setinu).
Chcete-li zjistit poloměr, vydělte obvod 2π, máme r = C / (2π) r = 18 stop / (2 * 3.14) r ≈ 18 stop / 6.28 r ≈ 2.87 stop (zaokrouhleno na nejbližší setinu).
![]() Nyní, abyste zjistili průměr, jednoduše zdvojnásobte poloměr: Průměr = 2 * Průměr poloměru ≈ 2 * 2.87 stopy Průměr ≈ 5.74 stopy. Piknikový stůl tedy musí mít průměr přibližně 5.74 stop
Nyní, abyste zjistili průměr, jednoduše zdvojnásobte poloměr: Průměr = 2 * Průměr poloměru ≈ 2 * 2.87 stopy Průměr ≈ 5.74 stopy. Piknikový stůl tedy musí mít průměr přibližně 5.74 stop
 Klíčové jídlo s sebou
Klíčové jídlo s sebou
![]() AhaSlides
AhaSlides ![]() je nejlepší interaktivní tvůrce kvízů, který lze použít pro účely vzdělávání, školení nebo zábavy. Podívejte se AhaSlides hned se osvobodit
je nejlepší interaktivní tvůrce kvízů, který lze použít pro účely vzdělávání, školení nebo zábavy. Podívejte se AhaSlides hned se osvobodit ![]() přizpůsobitelné šablony
přizpůsobitelné šablony![]() a pokročilé funkce!
a pokročilé funkce!
 Nejčastější dotazy
Nejčastější dotazy
![]() Co je 2πr kruhu?
Co je 2πr kruhu?
![]() 2πr je vzorec pro obvod kruhu. V tomto vzorci:
2πr je vzorec pro obvod kruhu. V tomto vzorci:
 "2" znamená, že berete dvojnásobek délky poloměru. Obvod je vzdálenost kolem kruhu, takže musíte kruh obejít jednou a pak znovu, proto násobíme 2.
"2" znamená, že berete dvojnásobek délky poloměru. Obvod je vzdálenost kolem kruhu, takže musíte kruh obejít jednou a pak znovu, proto násobíme 2. "π" (pi) je matematická konstanta přibližně rovna 3.14159. Používá se proto, že představuje vztah mezi obvodem a průměrem kruhu.
"π" (pi) je matematická konstanta přibližně rovna 3.14159. Používá se proto, že představuje vztah mezi obvodem a průměrem kruhu. „r“ představuje poloměr kruhu, což je vzdálenost od středu kruhu k libovolnému bodu na jeho obvodu.
„r“ představuje poloměr kruhu, což je vzdálenost od středu kruhu k libovolnému bodu na jeho obvodu.
![]() Proč je obvod 2πr?
Proč je obvod 2πr?
![]() Vzorec pro obvod kruhu, C = 2πr, pochází z definice pí (π) a geometrických vlastností kruhu. Pi (π) představuje poměr obvodu kruhu k jeho průměru. Když vynásobíte poloměr (r) 2π, v podstatě vypočítáte vzdálenost kolem kruhu, což je definice obvodu.
Vzorec pro obvod kruhu, C = 2πr, pochází z definice pí (π) a geometrických vlastností kruhu. Pi (π) představuje poměr obvodu kruhu k jeho průměru. Když vynásobíte poloměr (r) 2π, v podstatě vypočítáte vzdálenost kolem kruhu, což je definice obvodu.
![]() Je obvod 3.14krát větší než poloměr?
Je obvod 3.14krát větší než poloměr?
![]() Ne, obvod není přesně 3.14 násobek poloměru. Vztah mezi obvodem a poloměrem kruhu je dán vzorcem C = 2πr. Zatímco π (pi) je přibližně 3.14159, obvod je 2 krát π krát poloměr. Obvod je tedy více než jen 3.14násobek poloměru; je to 2 krát π krát poloměr.
Ne, obvod není přesně 3.14 násobek poloměru. Vztah mezi obvodem a poloměrem kruhu je dán vzorcem C = 2πr. Zatímco π (pi) je přibližně 3.14159, obvod je 2 krát π krát poloměr. Obvod je tedy více než jen 3.14násobek poloměru; je to 2 krát π krát poloměr.
![]() Ref:
Ref: ![]() Všeobecná kalkulačka |
Všeobecná kalkulačka | ![]() Prof
Prof







