![]() Conas Imlíne ciorcail a ríomh go beacht?
Conas Imlíne ciorcail a ríomh go beacht?
![]() Is eolas bunúsach agus riachtanach matamaitice é imlíne ciorcail a thugtar isteach sa bhunscoil nó sa mheánscoil. Tá máistreacht ar imlíne ciorcail riachtanach do mhic léinn a bhfuil sé beartaithe acu tabhairt faoi chúrsaí matamaitice níos airde sa scoil ard agus sa choláiste agus ullmhú le haghaidh scrúduithe caighdeánaithe ar nós SAT agus ACT.
Is eolas bunúsach agus riachtanach matamaitice é imlíne ciorcail a thugtar isteach sa bhunscoil nó sa mheánscoil. Tá máistreacht ar imlíne ciorcail riachtanach do mhic léinn a bhfuil sé beartaithe acu tabhairt faoi chúrsaí matamaitice níos airde sa scoil ard agus sa choláiste agus ullmhú le haghaidh scrúduithe caighdeánaithe ar nós SAT agus ACT.
![]() Tá an 10 gCeathrú Imlíne do Thráth na gCeist ciorcail san alt seo deartha chun do thuiscint ar aimsiú ga, trastomhas agus imlíne ciorcail a thástáil.
Tá an 10 gCeathrú Imlíne do Thráth na gCeist ciorcail san alt seo deartha chun do thuiscint ar aimsiú ga, trastomhas agus imlíne ciorcail a thástáil.
![]() Clár ábhair:
Clár ábhair:
 Ciorclán foirmle ciorcail
Ciorclán foirmle ciorcail
![]() Sula ndéanfaidh tú tástáil, déanaimis roinnt faisnéise ríthábhachtach a athchoimriú!
Sula ndéanfaidh tú tástáil, déanaimis roinnt faisnéise ríthábhachtach a athchoimriú!
 Conas imlíne ciorcail a fháil
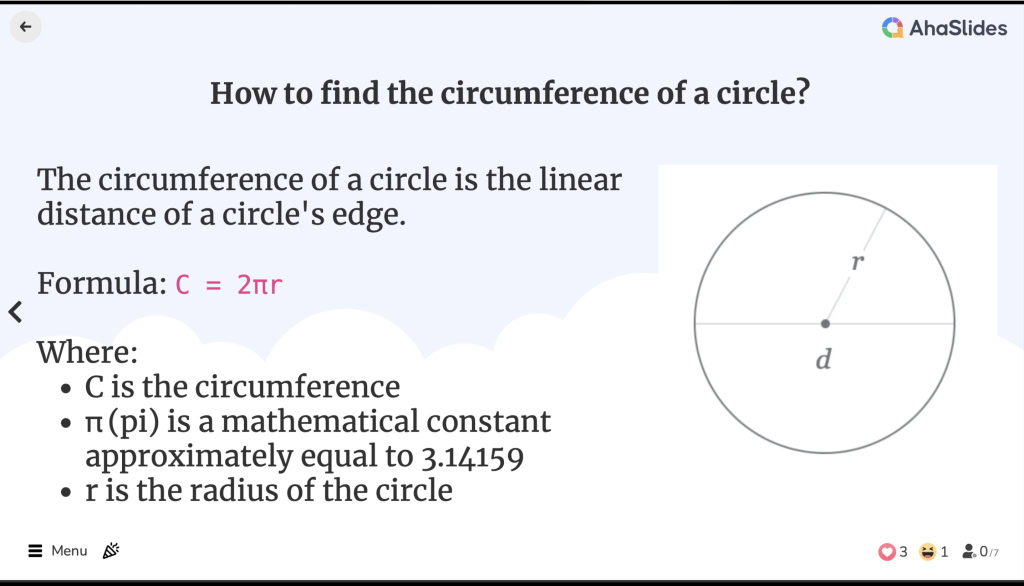
Conas imlíne ciorcail a fháil![]() Cad é imlíne ciorcail?
Cad é imlíne ciorcail?
![]() Is é imlíne ciorcail an fad líneach d'imeall ciorcail. Tá sé comhionann le himlíne cruth geoiméadrach, cé nach n-úsáidtear an téarma imlíne ach le haghaidh polagáin.
Is é imlíne ciorcail an fad líneach d'imeall ciorcail. Tá sé comhionann le himlíne cruth geoiméadrach, cé nach n-úsáidtear an téarma imlíne ach le haghaidh polagáin.
![]() Conas imlíne ciorcail a fháil?
Conas imlíne ciorcail a fháil?
![]() Is é imlíne foirmle ciorcail ná:
Is é imlíne foirmle ciorcail ná:
C = 2πr
![]() más rud é:
más rud é:
 Is é C an imlíne
Is é C an imlíne Is tairiseach matamaitice é π (pi) cothrom le 3.14159
Is tairiseach matamaitice é π (pi) cothrom le 3.14159 Is é r ga an chiorcail
Is é r ga an chiorcail
![]() Is é an ga an fad ó lár an chiorcail go pointe ar bith ar an imeall.
Is é an ga an fad ó lár an chiorcail go pointe ar bith ar an imeall.
![]() Tá an trastomhas dhá uair an ga, mar sin is féidir an imlíne a chur in iúl freisin mar:
Tá an trastomhas dhá uair an ga, mar sin is féidir an imlíne a chur in iúl freisin mar:
C = πd
![]() más rud é:
más rud é:
 Is é d an trastomhas
Is é d an trastomhas
![]() Mar shampla, más é 5 cm ga ciorcail, is é an imlíne ná:
Mar shampla, más é 5 cm ga ciorcail, is é an imlíne ná:
C = 2πr = 2π * 5 cm = 10π cm
![]() ≈ 31.4 cm (cothromaithe go 2 ionad dheachúlacha)
≈ 31.4 cm (cothromaithe go 2 ionad dheachúlacha)
 Tuilleadh Leideanna ó AhaSlides
Tuilleadh Leideanna ó AhaSlides
 70+ Tráth na gCeist Matamaitice Le hAghaidh Cleachtaí Spraoi sa Rang
70+ Tráth na gCeist Matamaitice Le hAghaidh Cleachtaí Spraoi sa Rang Na 10 gCluichí Matamaitice is Fearr sa Seomra Ranga do Dhaltaí Leamh K12
Na 10 gCluichí Matamaitice is Fearr sa Seomra Ranga do Dhaltaí Leamh K12 60 Smaointe Uafásach Ar Teasers Inchinn Do Dhaoine Fásta | Nuashonruithe 2023
60 Smaointe Uafásach Ar Teasers Inchinn Do Dhaoine Fásta | Nuashonruithe 2023
![]() AhaSlides is The Ultimate Quiz Maker
AhaSlides is The Ultimate Quiz Maker
![]() Déan cluichí idirghníomhacha ar an toirt lenár leabharlann teimpléid fairsing chun leadrán a mharú
Déan cluichí idirghníomhacha ar an toirt lenár leabharlann teimpléid fairsing chun leadrán a mharú

 Cluichí ar líne a Imirt Nuair a Leamh
Cluichí ar líne a Imirt Nuair a Leamh Imlíne tráth na gceist ciorcail
Imlíne tráth na gceist ciorcail
![]() Ceist 1: Más é 50 méadar imlíne linn snámha ciorclach, cad é a gha?
Ceist 1: Más é 50 méadar imlíne linn snámha ciorclach, cad é a gha?
![]() A. 7.95 méadar
A. 7.95 méadar
![]() B. 8.00 méadar
B. 8.00 méadar
![]() C. 15.91 méadar
C. 15.91 méadar
![]() D. 25 méadar
D. 25 méadar
A ![]() Freagra Ceart:
Freagra Ceart:
![]() A. 7.95 méadar
A. 7.95 méadar
![]() Míniú:
Míniú:
![]() Is féidir an ga a fháil tríd an bhfoirmle C = 2πr a atheagrú agus réiteach do r: r = C / (2π). Ag cur isteach an imlíne tugtha de 50 méadar agus thart ar π go 3.14, feicimid go bhfuil an ga thart ar 7.95 méadar.
Is féidir an ga a fháil tríd an bhfoirmle C = 2πr a atheagrú agus réiteach do r: r = C / (2π). Ag cur isteach an imlíne tugtha de 50 méadar agus thart ar π go 3.14, feicimid go bhfuil an ga thart ar 7.95 méadar.
![]() Ceist 2: Is é 14 orlach trastomhas ciorcail. Cad é a gha?
Ceist 2: Is é 14 orlach trastomhas ciorcail. Cad é a gha?
![]() A. 28 orlach
A. 28 orlach
![]() B.14 orlach
B.14 orlach
![]() C. 21 orlach
C. 21 orlach
![]() D. 7 orlach
D. 7 orlach
A ![]() Freagra Ceart:
Freagra Ceart:
![]() D. 7 orlach
D. 7 orlach
![]() Míniú:
Míniú:
![]() Ós rud é go bhfuil an trastomhas dhá oiread fad an ga (d = 2r), is féidir leat an ga a fháil tríd an trastomhas a roinnt ar 2 (r = d / 2).Sa chás seo, tríd an trastomhas tugtha 14 orlach a roinnt ar 2 táirgeacht a ga 7 orlach.
Ós rud é go bhfuil an trastomhas dhá oiread fad an ga (d = 2r), is féidir leat an ga a fháil tríd an trastomhas a roinnt ar 2 (r = d / 2).Sa chás seo, tríd an trastomhas tugtha 14 orlach a roinnt ar 2 táirgeacht a ga 7 orlach.

 Faigh imlíne ciorcail
Faigh imlíne ciorcail![]() Ceist 3: Cé acu ceann de na ráitis seo a leanas atá fíor faoin ghaolmhaireacht idir trastomhas agus imlíne ciorcail?
Ceist 3: Cé acu ceann de na ráitis seo a leanas atá fíor faoin ghaolmhaireacht idir trastomhas agus imlíne ciorcail?
![]() A. Is é an trastomhas leath an imlíne.
A. Is é an trastomhas leath an imlíne.
![]() B. Tá an trastomhas mar an gcéanna leis an imlíne.
B. Tá an trastomhas mar an gcéanna leis an imlíne.
![]() C. Tá an trastomhas dhá uair an imlíne.
C. Tá an trastomhas dhá uair an imlíne.
![]() D. Tá an trastomhas π uair an imlíne.
D. Tá an trastomhas π uair an imlíne.
A ![]() Freagra Ceart:
Freagra Ceart:
![]() A. Is é an trastomhas leath an imlíne.
A. Is é an trastomhas leath an imlíne.
![]() Míniú:
Míniú:
![]() Tá an trastomhas cothrom le 2 uair an ga, agus tá an imlíne cothrom le 2π huaire an ga. Dá bhrí sin, is é an trastomhas leath an imlíne.
Tá an trastomhas cothrom le 2 uair an ga, agus tá an imlíne cothrom le 2π huaire an ga. Dá bhrí sin, is é an trastomhas leath an imlíne.
![]() Ceist 4: Tá imlíne 6.28 slat ag an mbord a gcaithfimid suí air. Ní mór dúinn trastomhas an tábla a fháil.
Ceist 4: Tá imlíne 6.28 slat ag an mbord a gcaithfimid suí air. Ní mór dúinn trastomhas an tábla a fháil.
![]() A. 1 slat
A. 1 slat
![]() B. 2 slat
B. 2 slat
![]() C. 3 slat
C. 3 slat
![]() D. 4 slat
D. 4 slat
A ![]() Freagra Ceart:
Freagra Ceart:
![]() B. 2 slat
B. 2 slat
![]() Míniú:
Míniú:
![]() Ríomhtar imlíne ciorcail tríd an trastomhas a iolrú ar pi (π). Sa chás seo, tugtar an imlíne mar 6.28 slat. Chun an trastomhas a fháil, ní mór dúinn an imlíne a roinnt le pi. Má roinntear 6.28 slat ar pi, tugtar timpeall 2 shlat dúinn. Dá bhrí sin, tá trastomhas an tábla 2 shlat.
Ríomhtar imlíne ciorcail tríd an trastomhas a iolrú ar pi (π). Sa chás seo, tugtar an imlíne mar 6.28 slat. Chun an trastomhas a fháil, ní mór dúinn an imlíne a roinnt le pi. Má roinntear 6.28 slat ar pi, tugtar timpeall 2 shlat dúinn. Dá bhrí sin, tá trastomhas an tábla 2 shlat.
![]() Ceist 5: Tá imlíne 36 méadar ag gairdín ciorclach. Cad é gar-gha an ghairdín?
Ceist 5: Tá imlíne 36 méadar ag gairdín ciorclach. Cad é gar-gha an ghairdín?
![]() A. 3.14 méadar
A. 3.14 méadar
![]() B. 6 méadar
B. 6 méadar
![]() C. 9 méadar
C. 9 méadar
![]() D. 18 méadar
D. 18 méadar
A ![]() Freagra Ceart:
Freagra Ceart:
![]() C. 9 méadar
C. 9 méadar
![]() Míniú:
Míniú:
![]() Chun an ga a fháil, úsáid an fhoirmle don imlíne: C = 2πr. Atheagraigh an fhoirmle le réiteach don gha: r = C / (2π). Ag cur isteach an imlíne tugtha de 36 méadar agus ag baint úsáide as luach thart ar π mar 3.14, gheobhaidh tú r = 36 / (2 * 3.14) ≈ 9 méadar.
Chun an ga a fháil, úsáid an fhoirmle don imlíne: C = 2πr. Atheagraigh an fhoirmle le réiteach don gha: r = C / (2π). Ag cur isteach an imlíne tugtha de 36 méadar agus ag baint úsáide as luach thart ar π mar 3.14, gheobhaidh tú r = 36 / (2 * 3.14) ≈ 9 méadar.
![]() Ceist 6: Tá ga 8 méadar ag linn snámha ciorclach. Cad é an t-achar a thaistealaíonn snámhóir timpeall na linne agus é/í ag déanamh aon ghreim amháin?
Ceist 6: Tá ga 8 méadar ag linn snámha ciorclach. Cad é an t-achar a thaistealaíonn snámhóir timpeall na linne agus é/í ag déanamh aon ghreim amháin?
![]() A. 16 méadar
A. 16 méadar
![]() B. 25 méadar
B. 25 méadar
![]() C. 50 méadar
C. 50 méadar
![]() D. 100 méadar
D. 100 méadar
A ![]() Freagra Ceart:
Freagra Ceart:
![]() C. 50 méadar
C. 50 méadar
![]() Míniú:
Míniú:
![]() Chun an fad a thaistealaíonn snámhóir timpeall na linne ar feadh aon ghreim amháin a fháil, úsáideann tú an fhoirmle imlíne (C = 2πr). Sa chás seo, tá sé 2 * 3.14 * 8 méadar ≈ 50.24 méadar, atá thart ar 50 méadar.
Chun an fad a thaistealaíonn snámhóir timpeall na linne ar feadh aon ghreim amháin a fháil, úsáideann tú an fhoirmle imlíne (C = 2πr). Sa chás seo, tá sé 2 * 3.14 * 8 méadar ≈ 50.24 méadar, atá thart ar 50 méadar.
![]() Ceist 7: Agus an fonsa hula sa rang á thomhas, fuair grúpa C amach go raibh ga 7 n-orlach aige. Cad é imlíne an fonsa hula?
Ceist 7: Agus an fonsa hula sa rang á thomhas, fuair grúpa C amach go raibh ga 7 n-orlach aige. Cad é imlíne an fonsa hula?
![]() A. 39.6 orlach
A. 39.6 orlach
![]() B. 37.6 orlach
B. 37.6 orlach
![]() C. 47.6 orlach
C. 47.6 orlach
![]() D. 49.6 orlach
D. 49.6 orlach
A ![]() Freagra Ceart:
Freagra Ceart:
![]() C. 47.6 orlach
C. 47.6 orlach
![]() Míniú:
Míniú:
![]() Is féidir imlíne ciorcail a fháil leis an bhfoirmle C = 2πr, áit arb é r ga an chiorcail. Sa chás seo, tugtar ga an fonsa hula mar 7 orlach. Ag plugáil an luach seo isteach san fhoirmle, faighimid C = 2π(7) = 14π orlach. Ag thart ar π go 3.14, is féidir linn an imlíne a ríomh mar 14(3.14) = 43.96 orlach. Slánaithe go dtí an deichiú is gaire, is é 47.6 orlach an imlíne, rud a mheaitseálann an freagra a thugtar.
Is féidir imlíne ciorcail a fháil leis an bhfoirmle C = 2πr, áit arb é r ga an chiorcail. Sa chás seo, tugtar ga an fonsa hula mar 7 orlach. Ag plugáil an luach seo isteach san fhoirmle, faighimid C = 2π(7) = 14π orlach. Ag thart ar π go 3.14, is féidir linn an imlíne a ríomh mar 14(3.14) = 43.96 orlach. Slánaithe go dtí an deichiú is gaire, is é 47.6 orlach an imlíne, rud a mheaitseálann an freagra a thugtar.
![]() Ceist 8: Tá ga 10 méadar ag leathchiorcal. Cad é a imlíne?
Ceist 8: Tá ga 10 méadar ag leathchiorcal. Cad é a imlíne?
![]() A. 20 méadar
A. 20 méadar
![]() B. 15 méadar
B. 15 méadar
![]() C. 31.42 méadar
C. 31.42 méadar
![]() D. 62.84 méadar
D. 62.84 méadar
A ![]() Freagra Ceart:
Freagra Ceart:
![]() C. 31.42 méadar
C. 31.42 méadar
![]() Míniú:
Míniú:![]() Chun imlíne an leathchiorcail a fháil, ríomh leath imlíne ciorcail iomláin a bhfuil ga 10 méadar aige.
Chun imlíne an leathchiorcail a fháil, ríomh leath imlíne ciorcail iomláin a bhfuil ga 10 méadar aige.

 Imlíne shampla ciorcail
Imlíne shampla ciorcail![]() Ceist 9: Imríonn an fhoireann cispheile le liathróid a bhfuil ga 5.6 orlach aici. Cad é imlíne gach cispheile?
Ceist 9: Imríonn an fhoireann cispheile le liathróid a bhfuil ga 5.6 orlach aici. Cad é imlíne gach cispheile?
![]() A. 11.2 orlach
A. 11.2 orlach
![]() B. 17.6 orlach
B. 17.6 orlach
![]() C. 22.4 orlach
C. 22.4 orlach
![]() D. 35.2 orlach
D. 35.2 orlach
A ![]() Freagra Ceart:
Freagra Ceart:
![]() C. 22.4 orlach
C. 22.4 orlach
![]() Míniú:
Míniú:
![]() Is féidir leat an fhoirmle a úsáid le haghaidh imlíne ciorcail, arb é C = 2πr é. Is é 5.6 orlach an ga tugtha. Plug an luach seo isteach san fhoirmle, ní mór dúinn C = 2π * 5.6 orlach. C ≈ 2 * 3.14 * 5.6 orlach. C ≈ 11.2 * 5.6 orlach. C ≈ 22.4 orlach. Mar sin, tá imlíne gach cispheile thart ar 22.4 orlach. Léiríonn sé seo an fad timpeall na cispheile.
Is féidir leat an fhoirmle a úsáid le haghaidh imlíne ciorcail, arb é C = 2πr é. Is é 5.6 orlach an ga tugtha. Plug an luach seo isteach san fhoirmle, ní mór dúinn C = 2π * 5.6 orlach. C ≈ 2 * 3.14 * 5.6 orlach. C ≈ 11.2 * 5.6 orlach. C ≈ 22.4 orlach. Mar sin, tá imlíne gach cispheile thart ar 22.4 orlach. Léiríonn sé seo an fad timpeall na cispheile.
![]() Ceist 10: Bhí Sarah agus a beirt chairde ag tógáil bord ciorclach picnice le chéile. Bhí a fhios acu gur theastaigh imlíne 18 dtroigh uathu le go mbeadh siad ar fad ina suí go compordach timpeall an bhoird. Cén trastomhas a chaithfidh a bheith ar an mbord picnic chun an imlíne cheart a bhaint amach?
Ceist 10: Bhí Sarah agus a beirt chairde ag tógáil bord ciorclach picnice le chéile. Bhí a fhios acu gur theastaigh imlíne 18 dtroigh uathu le go mbeadh siad ar fad ina suí go compordach timpeall an bhoird. Cén trastomhas a chaithfidh a bheith ar an mbord picnic chun an imlíne cheart a bhaint amach?
![]() A. 3 troighe
A. 3 troighe
![]() B. 6 throigh
B. 6 throigh
![]() C. 9 troigh
C. 9 troigh
![]() D. 12 throigh
D. 12 throigh
A ![]() Freagra Ceart:
Freagra Ceart:
![]() B. 6 throigh
B. 6 throigh
![]() Míniú:
Míniú:
![]() Chun an ga a fháil, roinn an imlíne ar 2π, ní mór dúinn r = C / (2π) r = 18 troigh / (2 * 3.14) r ≈ 18 troigh / 6.28 r ≈ 2.87 troigh (slánaithe go dtí an céadú is gaire).
Chun an ga a fháil, roinn an imlíne ar 2π, ní mór dúinn r = C / (2π) r = 18 troigh / (2 * 3.14) r ≈ 18 troigh / 6.28 r ≈ 2.87 troigh (slánaithe go dtí an céadú is gaire).
![]() Anois, chun an trastomhas a fháil, níl le déanamh ach an ga a dhúbailt: Trastomhas = 2 * Trastomhas Ga ≈ 2 * 2.87 troigh Trastomhas ≈ 5.74 troigh. Mar sin, ní mór go mbeadh trastomhas de thart ar 5.74 troigh ar an mbord picnic
Anois, chun an trastomhas a fháil, níl le déanamh ach an ga a dhúbailt: Trastomhas = 2 * Trastomhas Ga ≈ 2 * 2.87 troigh Trastomhas ≈ 5.74 troigh. Mar sin, ní mór go mbeadh trastomhas de thart ar 5.74 troigh ar an mbord picnic
 Príomh-earraí beir leat
Príomh-earraí beir leat
![]() AhaSlides
AhaSlides ![]() an déantóir tráth na gceist idirghníomhach is fearr ar féidir hata a úsáid chun críocha oideachais, oiliúna nó siamsaíochta. Seiceáil amach AhaSlides láithreach a fháil saor in aisce
an déantóir tráth na gceist idirghníomhach is fearr ar féidir hata a úsáid chun críocha oideachais, oiliúna nó siamsaíochta. Seiceáil amach AhaSlides láithreach a fháil saor in aisce ![]() teimpléid inoiriúnaithe
teimpléid inoiriúnaithe![]() agus ardghnéithe!
agus ardghnéithe!
 Ceisteanna Coitianta
Ceisteanna Coitianta
![]() Cad é 2πr de chiorcal?
Cad é 2πr de chiorcal?
![]() Is é 2πr an fhoirmle le haghaidh imlíne ciorcail. Sa fhoirmle seo:
Is é 2πr an fhoirmle le haghaidh imlíne ciorcail. Sa fhoirmle seo:
 Léiríonn "2" go bhfuil tú ag tógáil dhá oiread fad an gha. Is é an imlíne an fad timpeall an chiorcail, mar sin ní mór duit dul timpeall an chiorcail arís agus arís eile, agus is é sin an fáth go ndéanaimid iolrú faoi 2.
Léiríonn "2" go bhfuil tú ag tógáil dhá oiread fad an gha. Is é an imlíne an fad timpeall an chiorcail, mar sin ní mór duit dul timpeall an chiorcail arís agus arís eile, agus is é sin an fáth go ndéanaimid iolrú faoi 2. Is tairiseach matamaitice é "π" (pi) arb ionann é agus 3.14159, a bheag nó a mhór. Úsáidtear é toisc go léiríonn sé an gaol idir imlíne agus trastomhas ciorcail.
Is tairiseach matamaitice é "π" (pi) arb ionann é agus 3.14159, a bheag nó a mhór. Úsáidtear é toisc go léiríonn sé an gaol idir imlíne agus trastomhas ciorcail. Seasann "r" do gha an chiorcail, is é sin an fad ó lár an chiorcail go dtí pointe ar bith ar a imlíne.
Seasann "r" do gha an chiorcail, is é sin an fad ó lár an chiorcail go dtí pointe ar bith ar a imlíne.
![]() Cén fáth go bhfuil imlíne 2πr?
Cén fáth go bhfuil imlíne 2πr?
![]() Tagann an fhoirmle le haghaidh imlíne ciorcail, C = 2πr, ón sainmhíniú ar pi (π) agus airíonna geoiméadracha ciorcail. Léiríonn pi (π) an cóimheas idir imlíne ciorcail agus a thrastomhas. Nuair a iolraíonn tú ga (r) faoi 2π, ríomhann tú go bunúsach an fad timpeall an chiorcail, arb é an sainmhíniú atá ar imlíne.
Tagann an fhoirmle le haghaidh imlíne ciorcail, C = 2πr, ón sainmhíniú ar pi (π) agus airíonna geoiméadracha ciorcail. Léiríonn pi (π) an cóimheas idir imlíne ciorcail agus a thrastomhas. Nuair a iolraíonn tú ga (r) faoi 2π, ríomhann tú go bunúsach an fad timpeall an chiorcail, arb é an sainmhíniú atá ar imlíne.
![]() An bhfuil an imlíne 3.14 huaire an ga?
An bhfuil an imlíne 3.14 huaire an ga?
![]() Ní hea, níl an imlíne díreach 3.14 uair an ga. Tugtar an gaol idir imlíne agus ga ciorcail leis an bhfoirmle C = 2πr. Cé go bhfuil π (pi) thart ar 3.14159, tá an imlíne 2 uair π huaire an ga. Mar sin, tá an imlíne níos mó ná 3.14 uair an ga; tá sé 2 uair π an ga.
Ní hea, níl an imlíne díreach 3.14 uair an ga. Tugtar an gaol idir imlíne agus ga ciorcail leis an bhfoirmle C = 2πr. Cé go bhfuil π (pi) thart ar 3.14159, tá an imlíne 2 uair π huaire an ga. Mar sin, tá an imlíne níos mó ná 3.14 uair an ga; tá sé 2 uair π an ga.
![]() Tag:
Tag: ![]() Omni Áireamhán |
Omni Áireamhán | ![]() Proprof
Proprof







