Как точно рассчитать длину окружности?
Длина окружности — это базовые и необходимые математические знания, которые вводятся в начальной или средней школе. Освоение окружности необходимо учащимся, которые планируют изучать более сложные курсы математики в средней школе и колледже и готовятся к стандартным экзаменам, таким как SAT и ACT.
Тест «10 окружностей круга» в этой статье предназначен для того, чтобы проверить ваше понимание того, как найти радиус, диаметр и окружность круга.
Содержание:
Формула окружности круга
Прежде чем пройти тест, давайте подведем итоги важной информации!
Как найти длину окружностиЧто такое окружность круга?
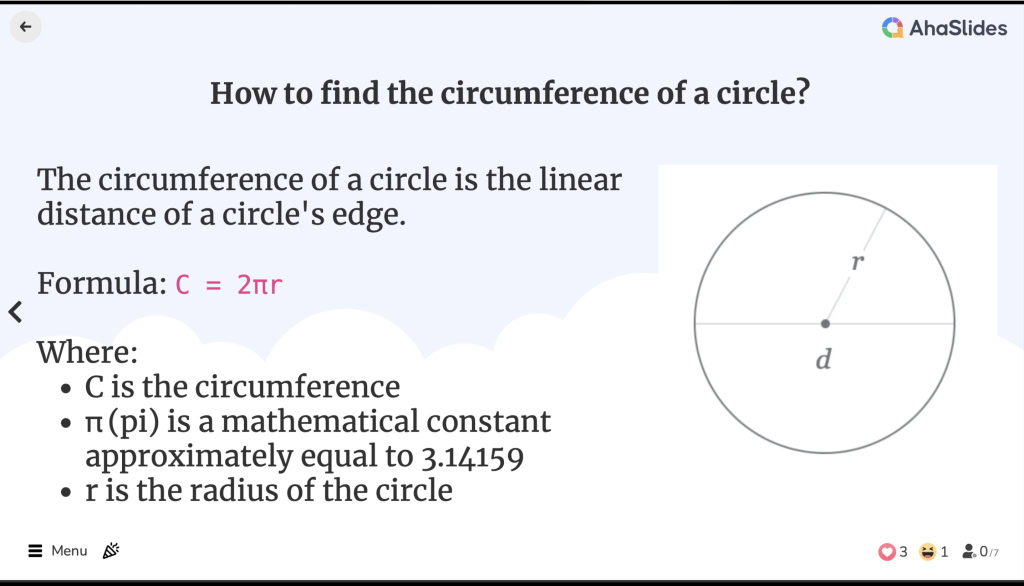
Длина окружности — это линейное расстояние от края окружности. Он эквивалентен периметру геометрической фигуры, хотя термин «периметр» используется только для многоугольников.
Как найти длину окружности?
Формула длины окружности:
C = 2πr
где:
- С — окружность
- π (пи) — математическая константа, примерно равная 3.14159.
- r - радиус окружности
Радиус — это расстояние от центра круга до любой точки на краю.
Диаметр в два раза больше радиуса, поэтому длину окружности можно также выразить как:
C = πd
где:
- d - диаметр
Например, если радиус круга равен 5 см, то длина окружности равна:
C = 2πr = 2π * 5 cm = 10π cm
≈ 31.4 см (округлено до 2 знаков после запятой)
Еще советы от AhaSlides
- 70+ вопросов викторины по математике для забавных упражнений в классе
- 10 лучших математических игр в классе для скучающих школьников K12
- 60 потрясающих идей по головоломке для взрослых | 2023 Обновления
AhaSlides это лучший создатель тестов
Создавайте интерактивные игры в одно мгновение с помощью нашей обширной библиотеки шаблонов, чтобы избавиться от скуки.
Онлайн-игры, в которые можно играть, когда скучноВикторина «Окружность круга»
Вопрос 1: Если окружность круглого бассейна составляет 50 метров, каков его радиус?
А. 7.95 метров
Б. 8.00 метров
С. 15.91 метров
Д. 25 метра
✅ Правильный ответ:
А. 7.95 метров
Объяснение:
Радиус можно найти, переставив формулу C = 2πr и решив для r: r = C/(2π). Подставив данную окружность в 50 метров и приблизив π к 3.14, мы находим радиус примерно 7.95 метра.
Вопрос 2: Диаметр круга 14 дюймов. Каков его радиус?
А. 28 дюйма
Б.14 дюймов
С. 21 дюймов
Д. 7 дюйма
✅ Правильный ответ:
Д. 7 дюйма
Объяснение:
Поскольку диаметр в два раза больше длины радиуса (d = 2r), вы можете найти радиус, разделив диаметр на 2 (r = d/2). В этом случае деление заданного диаметра в 14 дюймов на 2 дает радиус 7 дюймов.
Найдите длину окружностиВопрос 3. Какое из следующих утверждений верно относительно связи между диаметром и длиной окружности?
А. Диаметр равен половине окружности.
Б. Диаметр такой же, как окружность.
C. Диаметр в два раза больше окружности.
D. Диаметр в π раз больше окружности.
✅ Правильный ответ:
А. Диаметр равен половине окружности.
Объяснение:
Диаметр равен 2π радиусу, а длина окружности равна 2π радиусу. Следовательно, диаметр равен половине окружности.
Вопрос 4: Окружность стола, за которым мы должны сидеть, составляет 6.28 ярда. Нам нужно найти диаметр стола.
А. 1 ярд
Б. 2 ярда
С. 3 ярда
Д. 4 ярда
✅ Правильный ответ:
Б. 2 ярда
Объяснение:
Длина окружности вычисляется путем умножения диаметра на число Пи (π). В данном случае окружность равна 6.28 ярда. Чтобы найти диаметр, нам нужно длину окружности разделить на число Пи. Разделив 6.28 ярда на число Пи, получим примерно 2 ярда. Следовательно, диаметр стола равен 2 ярдам.
Вопрос 5: Круглый сад имеет окружность 36 метров. Каков примерный радиус сада?
А. 3.14 метров
Б. 6 метров
С. 9 метров
Д. 18 метра
✅ Правильный ответ:
С. 9 метров
Объяснение:
Чтобы найти радиус, используйте формулу длины окружности: C = 2πr. Переформулируйте формулу для определения радиуса: r = C/(2π). Подставив данную длину окружности в 36 метров и приняв приблизительное значение π как 3.14, вы получите r = 36/(2 * 3.14) ≈ 9 метров.
Вопрос 6: Круглый бассейн имеет радиус 8 метров. Какое приблизительное расстояние проходит пловец по бассейну за один круг?
А. 16 метров
Б. 25 метров
С. 50 метров
Д. 100 метра
✅ Правильный ответ:
С. 50 метров
Объяснение:
Чтобы найти расстояние, которое пловец проходит вокруг бассейна за один круг, используется формула длины окружности (C = 2πr). В данном случае это 2*3.14*8 метров ≈ 50.24 метра, что составляет примерно 50 метров.
Вопрос 7: При измерении обруча в классе группа C обнаружила, что его радиус составляет 7 дюймов. Какова окружность хула-хупа?
А. 39.6 дюйма
Б. 37.6 дюйма
С. 47.6 дюймов
Д. 49.6 дюйма
✅ Правильный ответ:
С. 47.6 дюймов
Объяснение:
Длину окружности можно найти по формуле C = 2πr, где r — радиус окружности. В данном случае радиус обруча равен 7 дюймам. Подставив это значение в формулу, получим C = 2π(7) = 14π дюймов. Приближая π к 3.14, мы можем вычислить длину окружности как 14 (3.14) = 43.96 дюйма. Округлив до ближайшей десятой, окружность составит 47.6 дюйма, что соответствует данному ответу.
Вопрос 8: Полукруг имеет радиус 10 метров. Каков его периметр?
А. 20 метров
Б. 15 метров
С. 31.42 метров
Д. 62.84 метра
✅ Правильный ответ:
С. 31.42 метров
Объяснение:Чтобы найти периметр полукруга, вычислите половину окружности полного круга радиусом 10 метров.
Пример окружности кругаВопрос 9: Баскетбольная команда играет мячом радиусом 5.6 дюйма. Какова окружность каждого баскетбольного мяча?
А. 11.2 дюйма
Б. 17.6 дюйма
С. 22.4 дюймов
Д. 35.2 дюйма
✅ Правильный ответ:
С. 22.4 дюймов
объяснение:
Вы можете использовать формулу длины окружности, которая равна C = 2πr. Данный радиус составляет 5.6 дюйма. Подставьте это значение в формулу, получим C = 2π * 5.6 дюйма. С ≈ 2*3.14*5.6 дюйма. С ≈ 11.2*5.6 дюйма. С ≈ 22.4 дюйма. Итак, окружность каждого баскетбольного мяча составляет примерно 22.4 дюйма. Это представляет собой расстояние вокруг баскетбольного мяча.
Вопрос 10: Сара и двое ее друзей строили круглый стол для пикника для своей компании. Они знали, что для того, чтобы всем им было удобно сидеть за столом, им нужна окружность в 18 футов. Какой диаметр должен иметь стол для пикника, чтобы его окружность была правильной?
А. 3 фута
Б. 6 футов
С. 9 футов
Д. 12 футов
✅ Правильный ответ:
Б. 6 футов
Объяснение:
Чтобы найти радиус, разделите длину окружности на 2π, получим r = C/(2π) r = 18 футов/(2*3.14) r ≈ 18 футов/6.28 r ≈ 2.87 фута (округляем до сотых).
Теперь, чтобы найти диаметр, просто удвойте радиус: Диаметр = 2 * Радиус. Диаметр ≈ 2 * 2.87 фута. Диаметр ≈ 5.74 фута. Итак, стол для пикника должен иметь диаметр примерно 5.74 фута.
Основные вынос
AhaSlides это лучший интерактивный конструктор тестов, который можно использовать в образовательных, обучающих или развлекательных целях. Проверьте AhaSlides немедленно освободиться настраиваемые шаблоныи расширенные функции!
Часто задаваемые вопросы
Что такое 2πr круга?
2πr — формула длины окружности. В этой формуле:
- «2» означает, что вы берете двойную длину радиуса. Окружность — это расстояние по кругу, поэтому нужно один раз обойти круг, поэтому и умножаем на 2.
- «π» (пи) — математическая константа, примерно равная 3.14159. Он используется потому, что представляет собой соотношение между длиной окружности и диаметром круга.
- «r» представляет собой радиус круга, который представляет собой расстояние от центра круга до любой точки на его окружности.
Почему длина окружности равна 2πr?
Формула длины окружности C = 2πr основана на определении числа пи (π) и геометрических свойствах круга. Пи (π) представляет собой отношение длины окружности к ее диаметру. Когда вы умножаете радиус (r) на 2π, вы, по сути, вычисляете расстояние вокруг круга, которое и является определением длины окружности.
Длина окружности в 3.14 раз больше радиуса?
Нет, длина окружности не в 3.14 раза больше радиуса. Связь между длиной окружности и радиусом круга определяется формулой C = 2πr. Хотя π (пи) примерно равно 3.14159, длина окружности в 2 раза превышает радиус, умноженный на π. Итак, окружность более чем в 3.14 раза превышает радиус; это в 2 раза больше π радиуса.
Ref: Омни Какулятор | Проф.
Теги: Идея викторины
