![]() Ինչպե՞ս ճշգրիտ հաշվարկել շրջանագծի շրջագիծը:
Ինչպե՞ս ճշգրիտ հաշվարկել շրջանագծի շրջագիծը:
![]() Շրջանակի շրջագիծը հիմնական և պահանջվող մաթեմատիկական գիտելիքներն են, որոնք ներդրվել են տարրական կամ միջին դպրոցում: Շրջանակի շրջագիծը տիրապետելը կարևոր է ուսանողների համար, ովքեր նախատեսում են մաթեմատիկայի ավելի առաջադեմ դասընթացներ անցնել ավագ դպրոցում և քոլեջում և պատրաստվել ստանդարտացված քննություններին, ինչպիսիք են SAT-ը և ACT-ը:
Շրջանակի շրջագիծը հիմնական և պահանջվող մաթեմատիկական գիտելիքներն են, որոնք ներդրվել են տարրական կամ միջին դպրոցում: Շրջանակի շրջագիծը տիրապետելը կարևոր է ուսանողների համար, ովքեր նախատեսում են մաթեմատիկայի ավելի առաջադեմ դասընթացներ անցնել ավագ դպրոցում և քոլեջում և պատրաստվել ստանդարտացված քննություններին, ինչպիսիք են SAT-ը և ACT-ը:
![]() Այս հոդվածի 10 շրջանագծի շրջանակը վիկտորինան նախատեսված է ստուգելու ձեր պատկերացումները շրջանագծի շառավիղը, տրամագիծը և շրջագիծը գտնելու վերաբերյալ:
Այս հոդվածի 10 շրջանագծի շրջանակը վիկտորինան նախատեսված է ստուգելու ձեր պատկերացումները շրջանագծի շառավիղը, տրամագիծը և շրջագիծը գտնելու վերաբերյալ:
![]() Բովանդակություն:
Բովանդակություն:
 Շրջանակի բանաձևի շրջապատը
Շրջանակի բանաձևի շրջապատը
![]() Նախքան թեստ անցնելը, եկեք ամփոփենք որոշ կարևոր տեղեկություններ:
Նախքան թեստ անցնելը, եկեք ամփոփենք որոշ կարևոր տեղեկություններ:
 Ինչպես գտնել շրջանագծի շրջագիծը
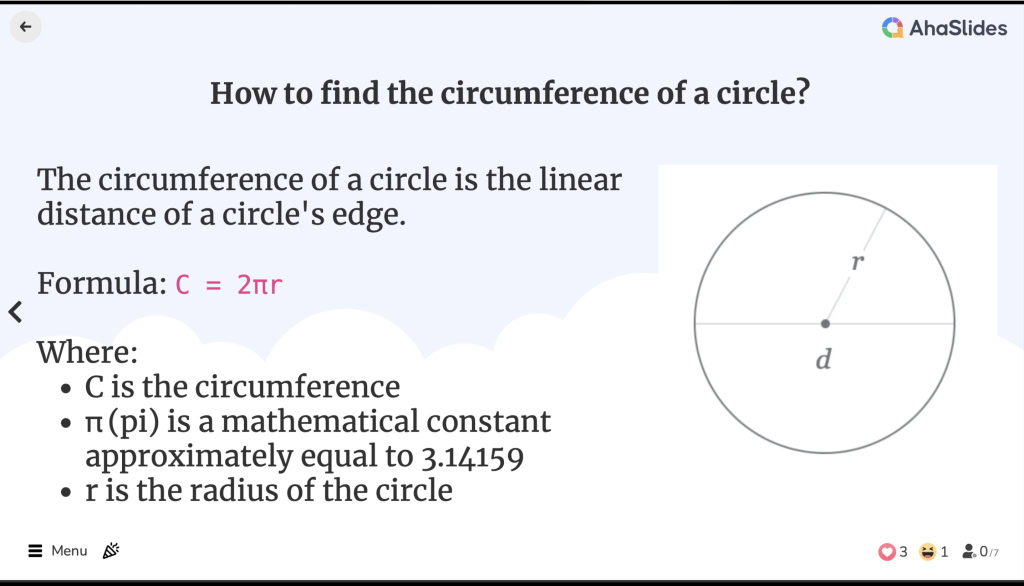
Ինչպես գտնել շրջանագծի շրջագիծը![]() Որքա՞ն է շրջանագծի շրջագիծը:
Որքա՞ն է շրջանագծի շրջագիծը:
![]() Շրջանակի շրջագիծը շրջանագծի եզրի գծային հեռավորությունն է։ Այն համարժեք է երկրաչափական ձևի պարագծին, թեև պարագիծ տերմինը օգտագործվում է միայն բազմանկյունների համար։
Շրջանակի շրջագիծը շրջանագծի եզրի գծային հեռավորությունն է։ Այն համարժեք է երկրաչափական ձևի պարագծին, թեև պարագիծ տերմինը օգտագործվում է միայն բազմանկյունների համար։
![]() Ինչպե՞ս գտնել շրջանագծի շրջագիծը:
Ինչպե՞ս գտնել շրջանագծի շրջագիծը:
![]() Շրջանակի բանաձևի շրջագիծը հետևյալն է.
Շրջանակի բանաձևի շրջագիծը հետևյալն է.
C = 2πr
![]() որտեղ
որտեղ
 C-ն շրջագիծն է
C-ն շրջագիծն է π (pi) մաթեմատիկական հաստատուն է մոտավորապես հավասար 3.14159-ի
π (pi) մաթեմատիկական հաստատուն է մոտավորապես հավասար 3.14159-ի r-ը շրջանագծի շառավիղն է
r-ը շրջանագծի շառավիղն է
![]() Շառավիղը շրջանագծի կենտրոնից մինչև եզրի ցանկացած կետ հեռավորությունն է:
Շառավիղը շրջանագծի կենտրոնից մինչև եզրի ցանկացած կետ հեռավորությունն է:
![]() Տրամագիծը կրկնակի է շառավղից, ուստի շրջագիծը կարող է արտահայտվել նաև հետևյալ կերպ.
Տրամագիծը կրկնակի է շառավղից, ուստի շրջագիծը կարող է արտահայտվել նաև հետևյալ կերպ.
C = πd
![]() որտեղ
որտեղ
 d-ն տրամագիծն է
d-ն տրամագիծն է
![]() Օրինակ, եթե շրջանագծի շառավիղը 5 սմ է, ապա շրջագիծը հետևյալն է.
Օրինակ, եթե շրջանագծի շառավիղը 5 սմ է, ապա շրջագիծը հետևյալն է.
C = 2πr = 2π * 5 cm = 10π cm
![]() ≈ 31.4 սմ (կլորացվում է 2 տասնորդական թվով)
≈ 31.4 սմ (կլորացվում է 2 տասնորդական թվով)
 Լրացուցիչ խորհուրդներ AhaSlides
Լրացուցիչ խորհուրդներ AhaSlides
 70+ մաթեմատիկական վիկտորինայի հարցեր դասարանում զվարճալի վարժությունների համար
70+ մաթեմատիկական վիկտորինայի հարցեր դասարանում զվարճալի վարժությունների համար 10 Լավագույն դասարանային մաթեմատիկայի խաղեր Bored K12 ուսանողների համար
10 Լավագույն դասարանային մաթեմատիկայի խաղեր Bored K12 ուսանողների համար 60 ապշեցուցիչ գաղափարներ մեծահասակների համար ուղեղային զնգոցների մասին | 2023 Թարմացումներ
60 ապշեցուցիչ գաղափարներ մեծահասակների համար ուղեղային զնգոցների մասին | 2023 Թարմացումներ
![]() AhaSlides The Ultimate Quiz Maker-ն է
AhaSlides The Ultimate Quiz Maker-ն է
![]() Մի ակնթարթում պատրաստեք ինտերակտիվ խաղեր մեր ընդարձակ կաղապարների գրադարանի միջոցով՝ ձանձրույթը վերացնելու համար
Մի ակնթարթում պատրաստեք ինտերակտիվ խաղեր մեր ընդարձակ կաղապարների գրադարանի միջոցով՝ ձանձրույթը վերացնելու համար

 Օնլայն խաղեր խաղալու համար, երբ ձանձրանում եք
Օնլայն խաղեր խաղալու համար, երբ ձանձրանում եք Շրջանակի վիկտորինա
Շրջանակի վիկտորինա
![]() Հարց 1. Եթե շրջանաձև լողավազանի շրջագիծը 50 մետր է, ապա որքա՞ն է նրա շառավիղը:
Հարց 1. Եթե շրջանաձև լողավազանի շրջագիծը 50 մետր է, ապա որքա՞ն է նրա շառավիղը:
![]() Ա.7.95 մետր
Ա.7.95 մետր
![]() B. 8.00 մետր
B. 8.00 մետր
![]() C. 15.91 մետր
C. 15.91 մետր
![]() D. 25 մետր
D. 25 մետր
✅ ![]() Ճիշտ պատասխան:
Ճիշտ պատասխան:
![]() Ա.7.95 մետր
Ա.7.95 մետր
![]() Բացատրությունը.
Բացատրությունը.
![]() Շառավիղը կարելի է գտնել՝ վերադասավորելով C = 2πr բանաձևը և լուծելով r՝ r = C / (2π): Միացնելով 50 մետր տրված շրջագիծը և մոտավորելով π 3.14-ին, մենք գտնում ենք, որ շառավիղը մոտավորապես 7.95 մետր է:
Շառավիղը կարելի է գտնել՝ վերադասավորելով C = 2πr բանաձևը և լուծելով r՝ r = C / (2π): Միացնելով 50 մետր տրված շրջագիծը և մոտավորելով π 3.14-ին, մենք գտնում ենք, որ շառավիղը մոտավորապես 7.95 մետր է:
![]() Հարց 2. Շրջանի տրամագիծը 14 դյույմ է: Որքա՞ն է նրա շառավիղը:
Հարց 2. Շրջանի տրամագիծը 14 դյույմ է: Որքա՞ն է նրա շառավիղը:
![]() A. 28 դյույմ
A. 28 դյույմ
![]() B.14 դյույմ
B.14 դյույմ
![]() C. 21 դյույմ
C. 21 դյույմ
![]() D. 7 դյույմ
D. 7 դյույմ
✅ ![]() Ճիշտ պատասխան:
Ճիշտ պատասխան:
![]() D. 7 դյույմ
D. 7 դյույմ
![]() Բացատրությունը.
Բացատրությունը.
![]() Քանի որ տրամագիծը երկու անգամ մեծ է շառավղի երկարությունից (d = 2r), դուք կարող եք գտնել շառավիղը՝ տրամագիծը բաժանելով 2-ի (r = d / 2): Այս դեպքում, տրված 14 դյույմ տրամագիծը բաժանելով 2-ի, ստացվում է. շառավիղը 7 դյույմ:
Քանի որ տրամագիծը երկու անգամ մեծ է շառավղի երկարությունից (d = 2r), դուք կարող եք գտնել շառավիղը՝ տրամագիծը բաժանելով 2-ի (r = d / 2): Այս դեպքում, տրված 14 դյույմ տրամագիծը բաժանելով 2-ի, ստացվում է. շառավիղը 7 դյույմ:

 Գտե՛ք շրջանագծի շրջագիծը
Գտե՛ք շրջանագծի շրջագիծը![]() Հարց 3. Հետևյալ պնդումներից ո՞րն է ճիշտ շրջանագծի տրամագծի և շրջագծի փոխհարաբերության վերաբերյալ:
Հարց 3. Հետևյալ պնդումներից ո՞րն է ճիշտ շրջանագծի տրամագծի և շրջագծի փոխհարաբերության վերաբերյալ:
![]() Ա. Տրամագիծը շրջագծի կեսն է:
Ա. Տրամագիծը շրջագծի կեսն է:
![]() B. Տրամագիծը նույնն է, ինչ շրջագիծը:
B. Տրամագիծը նույնն է, ինչ շրջագիծը:
![]() C. Տրամագիծը կրկնակի է շրջագծից:
C. Տրամագիծը կրկնակի է շրջագծից:
![]() D. Տրամագիծը π-ապատիկ է շրջագծին:
D. Տրամագիծը π-ապատիկ է շրջագծին:
✅ ![]() Ճիշտ պատասխան:
Ճիշտ պատասխան:
![]() Ա. Տրամագիծը շրջագծի կեսն է:
Ա. Տրամագիծը շրջագծի կեսն է:
![]() Բացատրությունը.
Բացատրությունը.
![]() Տրամագիծը հավասար է շառավիղի 2 անգամ, իսկ շրջագիծը հավասար է շառավիղից 2π անգամ։ Հետեւաբար, տրամագիծը շրջագծի կեսն է:
Տրամագիծը հավասար է շառավիղի 2 անգամ, իսկ շրջագիծը հավասար է շառավիղից 2π անգամ։ Հետեւաբար, տրամագիծը շրջագծի կեսն է:
![]() Հարց 4. Սեղանը, որի վրա պետք է նստենք, ունի 6.28 յարդ շրջագիծ: Մենք պետք է գտնենք սեղանի տրամագիծը:
Հարց 4. Սեղանը, որի վրա պետք է նստենք, ունի 6.28 յարդ շրջագիծ: Մենք պետք է գտնենք սեղանի տրամագիծը:
![]() Ա. 1 բակ
Ա. 1 բակ
![]() B. 2 բակ
B. 2 բակ
![]() C. 3 բակ
C. 3 բակ
![]() D. 4 բակ
D. 4 բակ
✅ ![]() Ճիշտ պատասխան:
Ճիշտ պատասխան:
![]() B. 2 բակ
B. 2 բակ
![]() Բացատրությունը.
Բացատրությունը.
![]() Շրջանակի շրջագիծը հաշվարկվում է տրամագիծը բազմապատկելով pi-ով (π): Այս դեպքում շրջագիծը տրվում է 6.28 յարդ: Տրամագիծը գտնելու համար մենք պետք է շրջագիծը բաժանենք pi-ի: 6.28 յարդը պ-ի վրա բաժանելը մեզ տալիս է մոտավորապես 2 յարդ: Հետեւաբար, սեղանի տրամագիծը 2 յարդ է:
Շրջանակի շրջագիծը հաշվարկվում է տրամագիծը բազմապատկելով pi-ով (π): Այս դեպքում շրջագիծը տրվում է 6.28 յարդ: Տրամագիծը գտնելու համար մենք պետք է շրջագիծը բաժանենք pi-ի: 6.28 յարդը պ-ի վրա բաժանելը մեզ տալիս է մոտավորապես 2 յարդ: Հետեւաբար, սեղանի տրամագիծը 2 յարդ է:
![]() Հարց 5. շրջանաձև այգին ունի 36 մետր շրջագիծ: Որքա՞ն է այգու մոտավոր շառավիղը:
Հարց 5. շրջանաձև այգին ունի 36 մետր շրջագիծ: Որքա՞ն է այգու մոտավոր շառավիղը:
![]() Ա.3.14 մետր
Ա.3.14 մետր
![]() B. 6 մետր
B. 6 մետր
![]() C. 9 մետր
C. 9 մետր
![]() D. 18 մետր
D. 18 մետր
✅ ![]() Ճիշտ պատասխան:
Ճիշտ պատասխան:
![]() C. 9 մետր
C. 9 մետր
![]() Բացատրությունը.
Բացատրությունը.
![]() Շառավիղը գտնելու համար օգտագործեք շրջագծի բանաձևը՝ C = 2πr: Վերադասավորե՛ք շառավիղը լուծելու բանաձևը՝ r = C / (2π): Միացնելով տրված 36 մետր շրջագիծը և օգտագործելով π-ի մոտավոր արժեքը որպես 3.14, դուք ստանում եք r = 36 / (2 * 3.14) ≈ 9 մետր:
Շառավիղը գտնելու համար օգտագործեք շրջագծի բանաձևը՝ C = 2πr: Վերադասավորե՛ք շառավիղը լուծելու բանաձևը՝ r = C / (2π): Միացնելով տրված 36 մետր շրջագիծը և օգտագործելով π-ի մոտավոր արժեքը որպես 3.14, դուք ստանում եք r = 36 / (2 * 3.14) ≈ 9 մետր:
![]() Հարց 6. շրջանաձև լողավազանն ունի 8 մետր շառավիղ: Ո՞րն է մոտավոր հեռավորությունը, որը լողորդը անցնում է լողավազանի շուրջ մեկ պտույտ կատարելիս:
Հարց 6. շրջանաձև լողավազանն ունի 8 մետր շառավիղ: Ո՞րն է մոտավոր հեռավորությունը, որը լողորդը անցնում է լողավազանի շուրջ մեկ պտույտ կատարելիս:
![]() Ա.16 մետր
Ա.16 մետր
![]() B. 25 մետր
B. 25 մետր
![]() C. 50 մետր
C. 50 մետր
![]() D. 100 մետր
D. 100 մետր
✅ ![]() Ճիշտ պատասխան:
Ճիշտ պատասխան:
![]() C. 50 մետր
C. 50 մետր
![]() Բացատրությունը.
Բացատրությունը.
![]() Լողավազանի մեկ պտույտի ընթացքում լողորդի անցած տարածությունը գտնելու համար օգտագործեք շրջագծի բանաձևը (C = 2πr): Այս դեպքում դա 2 * 3.14 * 8 մետր ≈ 50.24 մետր է, որը մոտավորապես 50 մետր է:
Լողավազանի մեկ պտույտի ընթացքում լողորդի անցած տարածությունը գտնելու համար օգտագործեք շրջագծի բանաձևը (C = 2πr): Այս դեպքում դա 2 * 3.14 * 8 մետր ≈ 50.24 մետր է, որը մոտավորապես 50 մետր է:
![]() Հարց 7. Դասարանում հուլա հուպը չափելիս C խումբը հայտնաբերեց, որ այն ուներ 7 դյույմ շառավիղ: Որքա՞ն է հուլա հուպի շրջագիծը:
Հարց 7. Դասարանում հուլա հուպը չափելիս C խումբը հայտնաբերեց, որ այն ուներ 7 դյույմ շառավիղ: Որքա՞ն է հուլա հուպի շրջագիծը:
![]() A. 39.6 դյույմ
A. 39.6 դյույմ
![]() B. 37.6 դյույմ
B. 37.6 դյույմ
![]() C. 47.6 դյույմ
C. 47.6 դյույմ
![]() D. 49.6 դյույմ
D. 49.6 դյույմ
✅ ![]() Ճիշտ պատասխան:
Ճիշտ պատասխան:
![]() C. 47.6 դյույմ
C. 47.6 դյույմ
![]() Բացատրությունը.
Բացատրությունը.
![]() Շրջանակի շրջագիծը կարելի է գտնել օգտագործելով C = 2πr բանաձևը, որտեղ r-ը շրջանագծի շառավիղն է: Այս դեպքում hula hoop-ի շառավիղը տրվում է 7 դյույմ: Միացնելով այս արժեքը բանաձևի մեջ, մենք ստանում ենք C = 2π(7) = 14π դյույմ: Մոտավորելով π 3.14-ին, մենք կարող ենք շրջագիծը հաշվարկել որպես 14(3.14) = 43.96 դյույմ: Կլորացվում է մինչև տասներորդականը, շրջագիծը 47.6 դյույմ է, որը համապատասխանում է տրված պատասխանին։
Շրջանակի շրջագիծը կարելի է գտնել օգտագործելով C = 2πr բանաձևը, որտեղ r-ը շրջանագծի շառավիղն է: Այս դեպքում hula hoop-ի շառավիղը տրվում է 7 դյույմ: Միացնելով այս արժեքը բանաձևի մեջ, մենք ստանում ենք C = 2π(7) = 14π դյույմ: Մոտավորելով π 3.14-ին, մենք կարող ենք շրջագիծը հաշվարկել որպես 14(3.14) = 43.96 դյույմ: Կլորացվում է մինչև տասներորդականը, շրջագիծը 47.6 դյույմ է, որը համապատասխանում է տրված պատասխանին։
![]() Հարց 8. Կիսաշրջանն ունի 10 մետր շառավիղ: Որքա՞ն է նրա պարագիծը:
Հարց 8. Կիսաշրջանն ունի 10 մետր շառավիղ: Որքա՞ն է նրա պարագիծը:
![]() Ա.20 մետր
Ա.20 մետր
![]() B. 15 մետր
B. 15 մետր
![]() C. 31.42 մետր
C. 31.42 մետր
![]() D. 62.84 մետր
D. 62.84 մետր
✅ ![]() Ճիշտ պատասխան:
Ճիշտ պատասխան:
![]() C. 31.42 մետր
C. 31.42 մետր
![]() Բացատրությունը.
Բացատրությունը.![]() Կիսաշրջանի պարագիծը գտնելու համար հաշվարկեք 10 մետր շառավղով լրիվ շրջանագծի շրջագծի կեսը։
Կիսաշրջանի պարագիծը գտնելու համար հաշվարկեք 10 մետր շառավղով լրիվ շրջանագծի շրջագծի կեսը։

 Շրջանակի օրինակ
Շրջանակի օրինակ![]() Հարց 9. Բասկետբոլի թիմը խաղում է 5.6 դյույմ շառավղով գնդակով: Որքա՞ն է յուրաքանչյուր բասկետբոլի շրջագիծը:
Հարց 9. Բասկետբոլի թիմը խաղում է 5.6 դյույմ շառավղով գնդակով: Որքա՞ն է յուրաքանչյուր բասկետբոլի շրջագիծը:
![]() A. 11.2 դյույմ
A. 11.2 դյույմ
![]() B. 17.6 դյույմ
B. 17.6 դյույմ
![]() C. 22.4 դյույմ
C. 22.4 դյույմ
![]() D. 35.2 դյույմ
D. 35.2 դյույմ
✅ ![]() Ճիշտ պատասխան:
Ճիշտ պատասխան:
![]() C. 22.4 դյույմ
C. 22.4 դյույմ
![]() բացատրություն:
բացատրություն:
![]() Դուք կարող եք օգտագործել շրջանագծի շրջագծի բանաձևը, որը C = 2πr է: Տրված շառավիղը 5.6 դյույմ է։ Միացրեք այս արժեքը բանաձևի մեջ, մենք ունենք C = 2π * 5.6 դյույմ: C ≈ 2 * 3.14 * 5.6 դյույմ: C ≈ 11.2 * 5.6 դյույմ: C ≈ 22.4 դյույմ: Այսպիսով, յուրաքանչյուր բասկետբոլի շրջագիծը մոտավորապես 22.4 դյույմ է: Սա ներկայացնում է բասկետբոլի շուրջ տարածությունը:
Դուք կարող եք օգտագործել շրջանագծի շրջագծի բանաձևը, որը C = 2πr է: Տրված շառավիղը 5.6 դյույմ է։ Միացրեք այս արժեքը բանաձևի մեջ, մենք ունենք C = 2π * 5.6 դյույմ: C ≈ 2 * 3.14 * 5.6 դյույմ: C ≈ 11.2 * 5.6 դյույմ: C ≈ 22.4 դյույմ: Այսպիսով, յուրաքանչյուր բասկետբոլի շրջագիծը մոտավորապես 22.4 դյույմ է: Սա ներկայացնում է բասկետբոլի շուրջ տարածությունը:
![]() Հարց 10. Սառան և իր երկու ընկերները հավաքելու համար շրջանաձև պիկնիկի սեղան էին պատրաստում: Նրանք գիտեին, որ բոլորի համար սեղանի շուրջ հարմարավետ նստելու համար անհրաժեշտ է 18 ոտնաչափ շրջագիծ։ Ինչ տրամագիծ պետք է ունենա պիկնիկի սեղանը ճիշտ շրջագծի հասնելու համար:
Հարց 10. Սառան և իր երկու ընկերները հավաքելու համար շրջանաձև պիկնիկի սեղան էին պատրաստում: Նրանք գիտեին, որ բոլորի համար սեղանի շուրջ հարմարավետ նստելու համար անհրաժեշտ է 18 ոտնաչափ շրջագիծ։ Ինչ տրամագիծ պետք է ունենա պիկնիկի սեղանը ճիշտ շրջագծի հասնելու համար:
![]() A. 3 ոտնաչափ
A. 3 ոտնաչափ
![]() B. 6 ոտնաչափ
B. 6 ոտնաչափ
![]() C. 9 ոտնաչափ
C. 9 ոտնաչափ
![]() D. 12 ոտնաչափ
D. 12 ոտնաչափ
✅ ![]() Ճիշտ պատասխան:
Ճիշտ պատասխան:
![]() B. 6 ոտնաչափ
B. 6 ոտնաչափ
![]() Բացատրությունը.
Բացատրությունը.
![]() Շառավիղը գտնելու համար շրջագիծը բաժանեք 2π-ի, մենք ունենք r = C / (2π) r = 18 ոտնաչափ / (2 * 3.14) r ≈ 18 ոտնաչափ / 6.28 r ≈ 2.87 ֆուտ (կլորացվում է մինչև հարյուրերորդականը):
Շառավիղը գտնելու համար շրջագիծը բաժանեք 2π-ի, մենք ունենք r = C / (2π) r = 18 ոտնաչափ / (2 * 3.14) r ≈ 18 ոտնաչափ / 6.28 r ≈ 2.87 ֆուտ (կլորացվում է մինչև հարյուրերորդականը):
![]() Այժմ տրամագիծը գտնելու համար պարզապես կրկնապատկեք շառավիղը. Այսպիսով, պիկնիկի սեղանը պետք է ունենա մոտավորապես 2 ոտնաչափ տրամագիծ
Այժմ տրամագիծը գտնելու համար պարզապես կրկնապատկեք շառավիղը. Այսպիսով, պիկնիկի սեղանը պետք է ունենա մոտավորապես 2 ոտնաչափ տրամագիծ
 Հիմնական ճարպերը
Հիմնական ճարպերը
![]() AhaSlides
AhaSlides ![]() լավագույն ինտերակտիվ վիկտորինան ստեղծողն է, որը գլխարկը կարող է օգտագործվել կրթության, վերապատրաստման կամ զվարճանքի նպատակներով: Ստուգեք AhaSlides անմիջապես անվճար ստանալու համար
լավագույն ինտերակտիվ վիկտորինան ստեղծողն է, որը գլխարկը կարող է օգտագործվել կրթության, վերապատրաստման կամ զվարճանքի նպատակներով: Ստուգեք AhaSlides անմիջապես անվճար ստանալու համար ![]() հարմարեցված կաղապարներ
հարմարեցված կաղապարներ![]() և առաջադեմ առանձնահատկություններ:
և առաջադեմ առանձնահատկություններ:
 Հաճախակի տրվող հարցեր
Հաճախակի տրվող հարցեր
![]() Որքա՞ն է շրջանագծի 2πr-ը:
Որքա՞ն է շրջանագծի 2πr-ը:
![]() 2πr-ը շրջանագծի շրջագծի բանաձևն է: Այս բանաձեւում.
2πr-ը շրջանագծի շրջագծի բանաձևն է: Այս բանաձեւում.
 «2»-ը ցույց է տալիս, որ դուք վերցնում եք շառավղից երկու անգամ ավելի երկար: Շրջագիծը շրջանի շուրջ տարածությունն է, այնպես որ դուք պետք է մեկ անգամ և նորից շրջեք շրջանակը, այդ իսկ պատճառով մենք բազմապատկում ենք 2-ով:
«2»-ը ցույց է տալիս, որ դուք վերցնում եք շառավղից երկու անգամ ավելի երկար: Շրջագիծը շրջանի շուրջ տարածությունն է, այնպես որ դուք պետք է մեկ անգամ և նորից շրջեք շրջանակը, այդ իսկ պատճառով մենք բազմապատկում ենք 2-ով: «π» (pi) մաթեմատիկական հաստատուն է մոտավորապես հավասար 3.14159-ի։ Այն օգտագործվում է, քանի որ այն ներկայացնում է շրջանագծի և տրամագծի հարաբերությունը:
«π» (pi) մաթեմատիկական հաստատուն է մոտավորապես հավասար 3.14159-ի։ Այն օգտագործվում է, քանի որ այն ներկայացնում է շրջանագծի և տրամագծի հարաբերությունը: «r»-ը ներկայացնում է շրջանագծի շառավիղը, որը շրջանագծի կենտրոնից մինչև նրա շրջագծի ցանկացած կետ հեռավորությունն է:
«r»-ը ներկայացնում է շրջանագծի շառավիղը, որը շրջանագծի կենտրոնից մինչև նրա շրջագծի ցանկացած կետ հեռավորությունն է:
![]() Ինչու է շրջագիծը 2πr:
Ինչու է շրջագիծը 2πr:
![]() Շրջանակի շրջագծի բանաձևը՝ C = 2πr, բխում է pi (π) սահմանումից և շրջանագծի երկրաչափական հատկություններից։ Pi (π) ներկայացնում է շրջանագծի շրջագծի և նրա տրամագծի հարաբերությունը: Երբ շառավիղը (r) բազմապատկում եք 2π-ով, դուք ըստ էության հաշվում եք շրջանագծի շուրջ տարածությունը, որը շրջագծի սահմանումն է:
Շրջանակի շրջագծի բանաձևը՝ C = 2πr, բխում է pi (π) սահմանումից և շրջանագծի երկրաչափական հատկություններից։ Pi (π) ներկայացնում է շրջանագծի շրջագծի և նրա տրամագծի հարաբերությունը: Երբ շառավիղը (r) բազմապատկում եք 2π-ով, դուք ըստ էության հաշվում եք շրջանագծի շուրջ տարածությունը, որը շրջագծի սահմանումն է:
![]() Արդյո՞ք շրջագիծը 3.14 անգամ մեծ է շառավղից:
Արդյո՞ք շրջագիծը 3.14 անգամ մեծ է շառավղից:
![]() Ոչ, շրջագիծը շառավիղից ուղիղ 3.14 անգամ չէ։ Շրջագծի և շրջանագծի շառավիղի հարաբերությունը տրված է C = 2πr բանաձևով: Մինչ π (pi) մոտավորապես 3.14159 է, շրջագիծը 2 անգամ π է շառավիղից: Այսպիսով, շրջագիծը շառավղից ավելին է, քան 3.14 անգամ; դա շառավիղից 2 անգամ մեծ է π.
Ոչ, շրջագիծը շառավիղից ուղիղ 3.14 անգամ չէ։ Շրջագծի և շրջանագծի շառավիղի հարաբերությունը տրված է C = 2πr բանաձևով: Մինչ π (pi) մոտավորապես 3.14159 է, շրջագիծը 2 անգամ π է շառավիղից: Այսպիսով, շրջագիծը շառավղից ավելին է, քան 3.14 անգամ; դա շառավիղից 2 անգամ մեծ է π.
![]() Ref:
Ref: ![]() Omni հաշվիչ |
Omni հաշվիչ | ![]() պրոֆ
պրոֆ







