តើធ្វើដូចម្តេចដើម្បីគណនារង្វង់មូលយ៉ាងពិតប្រាកដ?
រង្វង់នៃរង្វង់គឺជាចំណេះដឹងគណិតវិទ្យាជាមូលដ្ឋាន និងចាំបាច់ដែលត្រូវបានណែនាំនៅក្នុងសាលាបឋមសិក្សា ឬមធ្យមសិក្សា។ ការធ្វើជាម្ចាស់នៃរង្វង់រង្វង់គឺចាំបាច់សម្រាប់សិស្សដែលមានគម្រោងបន្តវគ្គសិក្សាគណិតវិទ្យាកម្រិតខ្ពស់បន្ថែមទៀតនៅក្នុងវិទ្យាល័យ និងមហាវិទ្យាល័យ ហើយរៀបចំសម្រាប់ការប្រឡងតាមស្តង់ដារដូចជា SAT និង ACT ។
10 Circumference of a Circle Quiz នៅក្នុងអត្ថបទនេះត្រូវបានរចនាឡើងដើម្បីសាកល្បងការយល់ដឹងរបស់អ្នកក្នុងការស្វែងរកកាំ អង្កត់ផ្ចិត និងរង្វង់នៃរង្វង់មួយ។
តារាងមាតិកា:
បរិមាត្រនៃរូបមន្តរង្វង់
មុននឹងធ្វើតេស្ត សូមសង្ខេបព័ត៌មានសំខាន់ៗមួយចំនួន!
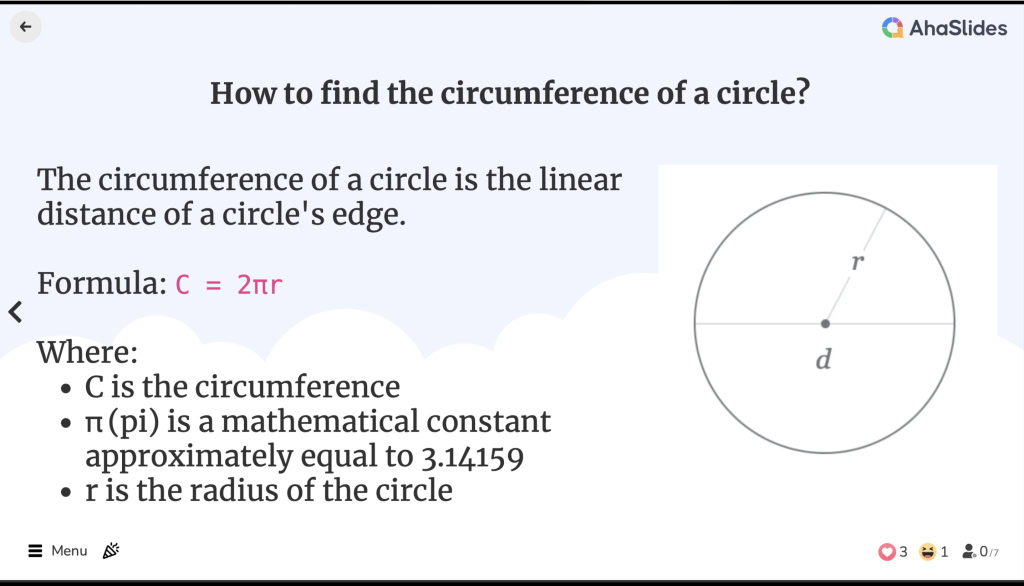
របៀបស្វែងរករង្វង់មូលតើរង្វង់មូលគឺជាអ្វី?
រង្វង់នៃរង្វង់គឺជាចម្ងាយលីនេអ៊ែរនៃគែមរង្វង់មួយ។ វាស្មើនឹងបរិមាត្រនៃរាងធរណីមាត្រ ទោះបីជាពាក្យបរិមាត្រត្រូវបានប្រើសម្រាប់តែពហុកោណប៉ុណ្ណោះ។
តើធ្វើដូចម្តេចដើម្បីរករង្វង់នៃរង្វង់មួយ?
រង្វង់នៃរូបមន្តរង្វង់គឺ៖
C = 2πr
ដែលជាកន្លែង:
- C គឺជារង្វង់
- π (pi) គឺជាចំនួនថេរគណិតវិទ្យាប្រហែលស្មើនឹង 3.14159
- r គឺជាកាំនៃរង្វង់
កាំគឺជាចម្ងាយពីចំណុចកណ្តាលនៃរង្វង់ទៅចំណុចណាមួយនៅលើគែម។
អង្កត់ផ្ចិតគឺពីរដងនៃកាំ ដូច្នេះបរិមាត្រក៏អាចត្រូវបានបញ្ជាក់ជា:
C = πd
ដែលជាកន្លែង:
- d គឺជាអង្កត់ផ្ចិត
ឧទាហរណ៍ ប្រសិនបើកាំនៃរង្វង់គឺ 5 សង់ទីម៉ែត្រ នោះរង្វង់គឺ៖
C = 2πr = 2π * 5 cm = 10π cm
≈ 31.4 សង់ទីម៉ែត្រ (បង្គត់ទៅ 2 ខ្ទង់ទសភាគ)
គន្លឹះច្រើនទៀតពី AhaSlides
- 70+ សំណួរគណិតវិទ្យាសម្រាប់លំហាត់រីករាយក្នុងថ្នាក់
- ហ្គេមគណិតវិទ្យាក្នុងថ្នាក់ល្អបំផុតចំនួន 10 សម្រាប់សិស្ស K12 ដែលធុញទ្រាន់
- គំនិតដ៏អស្ចារ្យចំនួន 60 ស្តីពីការបង្រៀនខួរក្បាលសម្រាប់មនុស្សពេញវ័យ | ការធ្វើបច្ចុប្បន្នភាពឆ្នាំ 2023
AhaSlides គឺជា Ultimate Quiz Maker
បង្កើតហ្គេមអន្តរកម្មភ្លាមៗជាមួយបណ្ណាល័យគំរូដ៏ទូលំទូលាយរបស់យើង ដើម្បីបំបាត់ភាពអផ្សុក
ហ្គេមអនឡាញដែលត្រូវលេងពេលអផ្សុករង្វង់នៃកម្រងសំណួររង្វង់
សំណួរទី១៖ ប្រសិនបើរង្វង់អាងហែលទឹកមានចម្ងាយ ៥០ម៉ែត្រ តើកាំរបស់វាជាអ្វី?
A. 7.95 ម៉ែត្រ
B. 8.00 ម៉ែត្រ
C. 15.91 ម៉ែត្រ
ឃ ៤.០ ម៉ែត្រ
✅ ចម្លើយត្រឹមត្រូវ:
A. 7.95 ម៉ែត្រ
ការពន្យល់:
កាំអាចត្រូវបានរកឃើញដោយការរៀបចំឡើងវិញនូវរូបមន្ត C = 2πr និងដោះស្រាយសម្រាប់ r: r = C / (2π) ។ ការដោតចូលទៅក្នុងរង្វង់ដែលបានផ្តល់ឱ្យ 50 ម៉ែត្រនិងប្រហាក់ប្រហែល π ដល់ 3.14 យើងរកឃើញកាំប្រហែល 7.95 ម៉ែត្រ។
សំណួរទី 2: អង្កត់ផ្ចិតនៃរង្វង់គឺ 14 អ៊ីញ។ តើកាំរបស់វាគឺជាអ្វី?
A. 28 អ៊ីញ
B.14 អ៊ីញ
គ. ២១ អ៊ីញ
ឃ ៧ អ៊ីញ
✅ ចម្លើយត្រឹមត្រូវ:
ឃ ៧ អ៊ីញ
ការពន្យល់:
ដោយសារអង្កត់ផ្ចិតគឺពីរដងនៃប្រវែងកាំ (d=2r) អ្នកអាចរកឃើញកាំដោយបែងចែកអង្កត់ផ្ចិតដោយ 2 (r=d/2)។ក្នុងករណីនេះ ការបែងចែកអង្កត់ផ្ចិតដែលបានផ្តល់ឱ្យ 14 អ៊ីញដោយ 2 ផ្តល់ផល កាំ 7 អ៊ីញ។
ស្វែងរកទំហំរង្វង់សំណួរទី 3៖ តើសេចក្តីថ្លែងការណ៍ខាងក្រោមមួយណាពិតអំពីទំនាក់ទំនងរវាងអង្កត់ផ្ចិត និងរង្វង់រង្វង់មួយ?
A. អង្កត់ផ្ចិតគឺពាក់កណ្តាលរង្វង់។
ខ.អង្កត់ផ្ចិតគឺដូចគ្នាទៅនឹងបរិមាត្រ។
C. អង្កត់ផ្ចិតគឺពីរដងនៃរង្វង់។
ឃ. អង្កត់ផ្ចិតគឺπដងនៃរង្វង់។
✅ ចម្លើយត្រឹមត្រូវ:
A. អង្កត់ផ្ចិតគឺពាក់កណ្តាលរង្វង់។
ការពន្យល់:
អង្កត់ផ្ចិតគឺស្មើនឹង 2 ដងនៃកាំខណៈពេលដែលរង្វង់គឺស្មើនឹង 2π ដងនៃកាំ។ ដូច្នេះអង្កត់ផ្ចិតគឺពាក់កណ្តាលរង្វង់។
សំណួរទី 4: តុដែលយើងត្រូវអង្គុយមានរង្វង់ 6.28 យ៉ាត។ យើងត្រូវស្វែងរកអង្កត់ផ្ចិតនៃតារាង។
ក.១ យ៉ាត
ខ.២ យ៉ាត
គ.៣ យ៉ាត
ឃ ៤ យ៉ាត
✅ ចម្លើយត្រឹមត្រូវ:
ខ.២ យ៉ាត
ការពន្យល់:
រង្វង់នៃរង្វង់ត្រូវបានគណនាដោយគុណអង្កត់ផ្ចិតដោយ pi (π) ។ ក្នុងករណីនេះបរិមាត្រត្រូវបានផ្តល់ឱ្យជា 6.28 យ៉ាត។ ដើម្បីស្វែងរកអង្កត់ផ្ចិត យើងត្រូវបែងចែករង្វង់ដោយ pi ។ ការបែងចែក 6.28 យ៉ាតដោយ pi ផ្តល់ឱ្យយើងប្រហែល 2 យ៉ាត។ ដូច្នេះអង្កត់ផ្ចិតនៃតុគឺ 2 យ៉ាត។
សំណួរទី 5: សួនរាងជារង្វង់មានរង្វង់ 36 ម៉ែត្រ។ តើកាំប្រហាក់ប្រហែលនៃសួនច្បារគឺជាអ្វី?
A. 3.14 ម៉ែត្រ
B. 6 ម៉ែត្រ
C. 9 ម៉ែត្រ
ឃ ៤.០ ម៉ែត្រ
✅ ចម្លើយត្រឹមត្រូវ:
C. 9 ម៉ែត្រ
ការពន្យល់:
ដើម្បីស្វែងរកកាំ សូមប្រើរូបមន្តសម្រាប់បរិមាត្រ៖ C = 2πr ។ រៀបចំរូបមន្តដើម្បីដោះស្រាយសម្រាប់កាំ៖ r = C / (2π) ។ ដោតក្នុងរង្វង់ដែលបានផ្តល់ឱ្យ 36 ម៉ែត្រនិងប្រើតម្លៃប្រហាក់ប្រហែលនៃπជា 3.14 អ្នកទទួលបាន r = 36 / (2 * 3.14) ≈ 9 ម៉ែត្រ។
សំណួរទី៦៖ អាងហែលទឹករាងជារង្វង់មានកាំ ៨ ម៉ែត្រ។ តើចម្ងាយប្រហាក់ប្រហែលដែលអ្នកហែលទឹកធ្វើដំណើរជុំវិញអាងទឹកនៅពេលបញ្ចប់ភ្លៅមួយ?
A. 16 ម៉ែត្រ
B. 25 ម៉ែត្រ
C. 50 ម៉ែត្រ
ឃ ៤.០ ម៉ែត្រ
✅ ចម្លើយត្រឹមត្រូវ:
C. 50 ម៉ែត្រ
ការពន្យល់:
ដើម្បីស្វែងរកចម្ងាយដែលអ្នកហែលទឹកធ្វើដំណើរជុំវិញអាងសម្រាប់ភ្លៅមួយ អ្នកអាចប្រើរូបមន្តរង្វង់ (C = 2πr) ។ ក្នុងករណីនេះវាមានទំហំ 2 * 3.14 * 8 ម៉ែត្រ≈ 50.24 ម៉ែត្រដែលមានប្រហែល 50 ម៉ែត្រ។
សំណួរទី 7: នៅពេលវាស់ hula hoop នៅក្នុងថ្នាក់ ក្រុម C បានរកឃើញថាវាមានកាំ 7 អ៊ីញ។ តើរង្វង់នៃ hula hoop គឺជាអ្វី?
A. 39.6 អ៊ីញ
ខ. ៣៧.៦ អ៊ីញ
គ. ២១ អ៊ីញ
ឃ ៧ អ៊ីញ
✅ ចម្លើយត្រឹមត្រូវ:
គ. ២១ អ៊ីញ
ការពន្យល់:
រង្វង់នៃរង្វង់អាចត្រូវបានរកឃើញដោយប្រើរូបមន្ត C = 2πr ដែល r ជាកាំនៃរង្វង់។ ក្នុងករណីនេះកាំនៃ hula hoop ត្រូវបានផ្តល់ជា 7 អ៊ីញ។ ការបញ្ចូលតម្លៃនេះទៅក្នុងរូបមន្ត យើងទទួលបាន C = 2π(7) = 14π អ៊ីញ។ ប្រមាណπ ទៅ 3.14 យើងអាចគណនារង្វង់ជា 14(3.14) = 43.96 អ៊ីញ។ បង្គត់ទៅភាគដប់ជិតបំផុត បរិមាត្រគឺ 47.6 អ៊ីង ដែលផ្គូផ្គងនឹងចម្លើយដែលបានផ្តល់ឱ្យ។
សំណួរទី ៨៖ រង្វង់មួយមានកាំ ១០ ម៉ែត្រ។ តើបរិវេណរបស់វាគឺជាអ្វី?
A. 20 ម៉ែត្រ
B. 15 ម៉ែត្រ
C. 31.42 ម៉ែត្រ
ឃ ៤.០ ម៉ែត្រ
✅ ចម្លើយត្រឹមត្រូវ:
C. 31.42 ម៉ែត្រ
ការពន្យល់:ដើម្បីស្វែងរកបរិវេណនៃរង្វង់មូល សូមគណនាពាក់កណ្តាលរង្វង់នៃរង្វង់ពេញដែលមានកាំ 10 ម៉ែត្រ។
រង្វង់នៃឧទាហរណ៍រង្វង់សំណួរទី 9៖ ក្រុមបាល់បោះលេងជាមួយបាល់ដែលមានកាំ 5.6 អ៊ីញ។ តើបាល់បោះនីមួយៗមានទំហំប៉ុនណា?
A. 11.2 អ៊ីញ
ខ. ៣៧.៦ អ៊ីញ
គ. ២១ អ៊ីញ
ឃ ៧ អ៊ីញ
✅ ចម្លើយត្រឹមត្រូវ:
គ. ២១ អ៊ីញ
ការពន្យល់:
អ្នកអាចប្រើរូបមន្តសម្រាប់រង្វង់នៃរង្វង់ដែលជា C = 2πr ។ កាំដែលបានផ្តល់ឱ្យគឺ 5.6 អ៊ីញ។ ដោតតម្លៃនេះទៅក្នុងរូបមន្ត យើងមាន C = 2π * 5.6 អ៊ីញ។ C ≈ 2 * 3.14 * 5.6 អ៊ីញ។ C ≈ 11.2 * 5.6 អ៊ីញ។ C ≈ 22.4 អ៊ីញ។ ដូច្នេះរង្វង់នៃបាល់បោះនីមួយៗគឺប្រហែល 22.4 អ៊ីញ។ នេះតំណាងឱ្យចម្ងាយជុំវិញបាល់បោះ។
សំណួរទី 10: សារ៉ា និងមិត្តភ័ក្តិពីរនាក់របស់នាងកំពុងសាងសង់តុអាហាររាងជារង្វង់សម្រាប់ការជួបជុំរបស់ពួកគេ។ ពួកគេបានដឹងថាដើម្បីឱ្យពួកគេទាំងអស់គ្នាអង្គុយជុំវិញតុបានស្រួល ពួកគេត្រូវការរង្វង់ 18 ហ្វីត។ តើតុអាហារគួរមានអង្កត់ផ្ចិតប៉ុន្មាន ដើម្បីសម្រេចបានរង្វង់ត្រឹមត្រូវ?
A. 3 ហ្វីត
B. 6 ហ្វីត
C. 9 ហ្វីត
ឃ ៦ ហ្វីត
✅ ចម្លើយត្រឹមត្រូវ:
B. 6 ហ្វីត
ការពន្យល់:
ដើម្បីរកកាំចែករង្វង់ដោយ 2π យើងមាន r = C / (2π) r = 18 ហ្វីត / (2 * 3.14) r ≈ 18 ហ្វីត / 6.28 r ≈ 2.87 ហ្វីត (បង្គត់ទៅរាប់រយជិតបំផុត) ។
ឥឡូវនេះ ដើម្បីស្វែងរកអង្កត់ផ្ចិត គ្រាន់តែបង្កើនកាំទ្វេដង៖ អង្កត់ផ្ចិត = 2 * កាំអង្កត់ផ្ចិត ≈ 2 * 2.87 ហ្វីត អង្កត់ផ្ចិត ≈ 5.74 ហ្វីត។ ដូច្នេះ តុអាហារត្រូវមានអង្កត់ផ្ចិតប្រហែល 5.74 ហ្វីត
ការចំណាយដ៏សំខាន់។
AhaSlides គឺជាអ្នកបង្កើតកម្រងសំណួរអន្តរកម្មដ៏ល្អបំផុតដែលមួកអាចត្រូវបានប្រើសម្រាប់ការអប់រំ ការបណ្តុះបណ្តាល ឬគោលបំណងកម្សាន្ត។ ពិនិត្យមើល AhaSlides ភ្លាមៗដើម្បីទទួលបានដោយឥតគិតថ្លៃ គំរូដែលអាចប្ដូរតាមបំណងបាន។និងមុខងារកម្រិតខ្ពស់!
សំណួរដែលគេបានសួរច្រើន
តើ 2πr នៃរង្វង់គឺជាអ្វី?
2πr គឺជារូបមន្តសម្រាប់រង្វង់មូល។ នៅក្នុងរូបមន្តនេះ៖
- "2" តំណាងឱ្យអ្នកកំពុងយកប្រវែងទ្វេដងនៃកាំ។ បរិមាត្រគឺជាចំងាយជុំវិញរង្វង់ ដូច្នេះអ្នកត្រូវដើរជុំវិញរង្វង់ម្តងហើយម្តងទៀត នោះហើយជាមូលហេតុដែលយើងគុណនឹង 2។
- "π" (pi) គឺជាចំនួនថេរគណិតវិទ្យាប្រហែលស្មើនឹង 3.14159 ។ វាត្រូវបានគេប្រើព្រោះវាតំណាងឱ្យទំនាក់ទំនងរវាងបរិមាត្រនិងអង្កត់ផ្ចិតនៃរង្វង់មួយ។
- "r" តំណាងឱ្យកាំនៃរង្វង់ដែលជាចម្ងាយពីកណ្តាលរង្វង់ទៅចំណុចណាមួយនៅលើរង្វង់របស់វា។
ហេតុអ្វីបានជារង្វង់គឺ 2πr?
រូបមន្តសម្រាប់បរិមាត្រនៃរង្វង់មួយ C = 2πr បានមកពីនិយមន័យនៃ pi (π) និងលក្ខណៈសម្បត្តិធរណីមាត្រនៃរង្វង់មួយ។ Pi (π) តំណាងឱ្យសមាមាត្រនៃរង្វង់រង្វង់ទៅអង្កត់ផ្ចិតរបស់វា។ នៅពេលអ្នកគុណកាំ (r) ដោយ 2π អ្នកត្រូវគណនាចំងាយជុំវិញរង្វង់ ដែលជានិយមន័យនៃរង្វង់។
តើរង្វង់មាន 3.14 ដងនៃកាំ?
ទេ រង្វង់មិនច្បាស់ 3.14 ដងនៃកាំនោះទេ។ ទំនាក់ទំនងរវាងបរិមាត្រ និងកាំនៃរង្វង់មួយត្រូវបានផ្តល់ដោយរូបមន្ត C = 2πr ។ ខណៈពេលដែល π (pi) គឺប្រហែល 3.14159 រង្វង់គឺ 2 ដង π ដងនៃកាំ។ ដូច្នេះ រង្វង់គឺច្រើនជាងកាំត្រឹមតែ 3.14 ដងប៉ុណ្ណោះ។ វាជា 2 ដង π ដងនៃកាំ។
យោង: ម៉ាស៊ីនគិតលេខ Omni | សាស្រ្តាចារ្យ
ស្លាក: គំនិតសំណួរ
